协同航迹时空安全性判断与重生成

2023-08-02 理论教育版权反馈

【摘要】：在3.3.3节中得到协同航迹后，还要对航迹间的时空安全进行判断，即保证沿协同航迹飞行的几枚导弹的最小间距不小于最小安全间距。继续对新航迹进行检测并重复上述步骤，直到满足安全防碰撞要求。例3-1假设4枚导弹协同飞行攻击同一个目标。其中，导弹#2的航迹最长，因此导弹#2的航迹不作调整。调整后，各导弹飞行航迹等长，飞行时间均为290.13 s。因此，这4条协同航迹是满足时空安全性要求的。

在3.3.3节中得到协同航迹后，还要对航迹间的时空安全进行判断，即保证沿协同航迹飞行的几枚导弹的最小间距不小于最小安全间距。

假设待检测的两条分段贝塞尔曲线航迹分别为B1（τ1）、B2（τ2），根据de Casteljau算法，可快速确定参数τ1、τ2对应的两点的坐标，由此可计算出两点之间的距离。针对τ1∈[0，1]、τ2∈[0，1]，可求得贝塞尔曲线上两点之间的最短距离dmin，如果dmin≥ds（ds为最小安全间距），则说明两条航迹安全；如果dmin＜ds，则说明两条航迹之间存在小于最小安全间距的点。

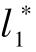接下来，利用式（3-5）计算两枚导弹从出发到不安全航迹点的飞行路程。在两枚导弹速度一致的前提下，若飞行路程不相等，则说明两枚导弹不会同时到达航迹间距最小点，无碰撞危险；若飞行路程相等则有碰撞危险，就要对其中一枚导弹的期望分段航迹长度进行调整。具体调整方法：假设原期望总长度l*由…若干期望分段长度组成，即l*=+…，若第一分段出现航迹碰撞危险点，则将原第一分段期望长度调整为 pagenumber_ebook=41,pagenumber_book=32 +ds，将第二段分段期望长度相应调整为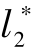-ds，并利用式（3-16）中的优化模型得到新的航迹。继续对新航迹进行检测并重复上述步骤，直到满足安全防碰撞要求。

例3-1　假设4枚导弹（#1、#2、#3和#4）协同飞行攻击同一个目标。目标位置为（60 km，50 km），4枚导弹的速度均为300 m/s，其初始点s、初始速度方向γs和要求的末端攻击方向γe、可用法向过载np等参数见表3-1。

表3-1　导弹的初始参数、可用过载及指定的攻击角度

pagenumber_ebook=42,pagenumber_book=33

假设导弹飞行的环境中有7个威胁区，其具体信息见表3-2。

表3-2　威胁区中心位置及安全半径

pagenumber_ebook=42,pagenumber_book=33

威胁区分布如图3-2所示。图中，按照德洛奈三角法连接威胁区的中心并绘出航迹节点（红色圆点）。

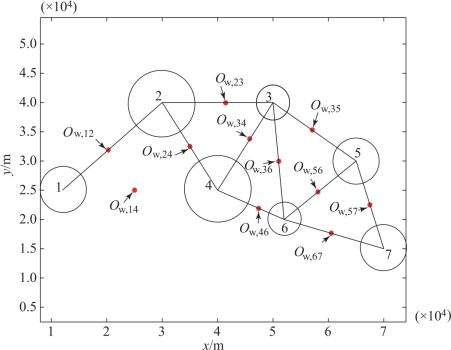
pagenumber_ebook=42,pagenumber_book=33

图3-2　战场威胁区及航迹节点

由图3-2可得，总的航迹节点集为

对于导弹#1，按照导弹相关航迹节点集定义，并根据各航迹节点与目标的距离按升序排列后得到含有目标的集合W′1为

同理，得到含有目标点的导弹#2、#3和#4的相关航迹节点集合分别为

pagenumber_ebook=43,pagenumber_book=34

采用MATLAB非线性约束优化函数fm incon对航迹进行优化，最大迭代次数为100；取优化变量的初值均为分段航迹起点与分段航迹终点间的距离；设导弹间的安全距离ds=50 m。规划出的四枚导弹的航迹如图3-3所示。

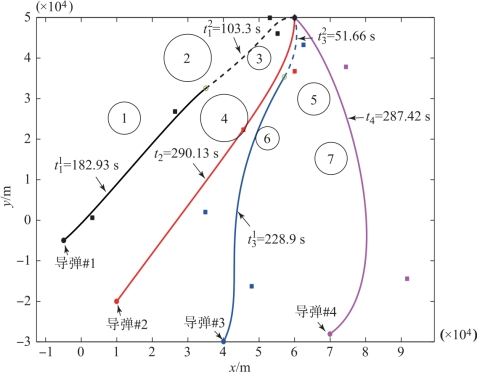
pagenumber_ebook=43,pagenumber_book=34

图3-3　导弹#1～#4的可行航迹

接下来，以导弹#1为例来说明具有攻击角度约束的航迹规划过程。根据2.2节中的算法，首先选取目标e作为分段终点，未得到满足约束的优化解，按照算法在集合W′1中向后选取Ow，23并判断其不满足情况①、②、③，故将其作为分段终点进行优化，但仍然未得到满足约束的优化解。因此，向后选取Ow，24且判断其不满足情况①、②、③，故将Ow，24作为分段终点进行优化，并得到了满足各约束条件的优化解。以Ow，24为分段起点，以目标为分段终点继续进行优化，得到优化解，最终得到的导弹#1的可行点集为Pick1={s1，Ow，24，e}。

对应的导弹#1的两段分段航迹如图3-3中黑色实线与黑色虚线所示，图中方形点表示各段贝塞尔曲线的控制点。导弹#1各段航迹对应的时间分别为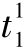 pagenumber_ebook=44,pagenumber_book=35 =182.93 s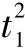，=103.3 s（上标表示航迹段号、下标表示导弹编号，下同），总飞行时长为t1=286.23 s。根据优化结果可知，第一段航迹的第二控制点位置为（3.12 km，0.68 km），第二段航迹的第三控制点位置为（52.97 km，50 km），由此可计算导弹的发射角度与攻击角度分别为

pagenumber_ebook=44,pagenumber_book=35

由此可见，规划好的贝塞尔曲线航迹满足以指定发射角发射导弹和以指定角度攻击目标的要求。

与此类似，对于导弹#2，其可行航迹点集为Pick2={s2，e}。因此，在图3-3中，导弹#2的航迹是一条连接起始点和终点的航迹，中间未经过其他航迹点。导弹#2的飞行时间为t2=290.13 s，航迹第三个控制点的位置为（60 km，36.71 km），满足攻击角度为90°的要求。导弹#3、#4的可行航迹节点集分别为Pick3={s3，Ow，35，e }，Pick4={s4，e}，导弹总飞行时间分别为t3=280.56 s、t4=287.42 s，导弹#3第二分段航迹以及导弹#4航迹的第三个控制点位置分别为（60.05 km，49.87 km）、（74.42 km，37.89 km），同样满足攻击角度110°和140°的要求。

导弹#1～#4的过载随参数τ的变化曲线如图3-4所示。

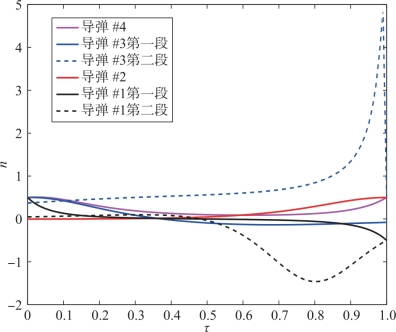
pagenumber_ebook=44,pagenumber_book=35

图3-4　导弹#1～#4的过载随参数τ的变化曲线

由图3-4可见，四枚导弹的最大需用过载均≤5，未超过可用过载且在航迹端点（即τ=0与τ=1）处的过载均≤0.5，满足要求。

由前述可知，四枚导弹的飞行航迹长度不相等，不能够实现时间协同。其中，导弹#2的航迹最长，因此导弹#2的航迹不作调整。由于各导弹速度均为300 m/s，故可将式（3-14）中航迹长度l替换为时间，其余各导弹的各段航迹飞行时间分别调整为

pagenumber_ebook=45,pagenumber_book=36

上述调整后的时间乘以速度得到的航迹长度即导弹#1、#3和#4各段航迹的期望长度。采用式（3-16）中的优化模型进行优化，得到如图3-5所示的调整后的航迹。

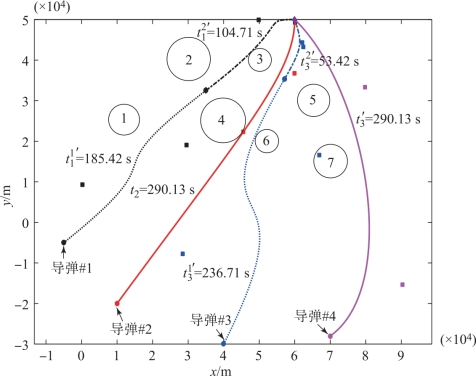
pagenumber_ebook=45,pagenumber_book=36

图3-5　导弹#2的原航迹与导弹#1、#3和#4调整后的航迹

由仿真结果可知，调整后的导弹#1、#3、#4的航迹依然满足发射角度与攻击角度的约束。但由于控制点位置的改变，新的航迹曲率和长度均有变化，因此在满足攻击角度约束的基础上进一步满足了攻击时间的约束。调整后，各导弹飞行航迹等长，飞行时间均为290.13 s。由于导弹#1、#3和#4要通过绕路来增大其航迹长度，因此调整后的3枚导弹的最大需用过载稍微增大，但仍小于可用过载，满足过载约束。如图3-5所示，四枚导弹除了在终点处相交，在其他航迹位置均不相交，且导弹#2、#3航迹中段的最小距离约为1.8 km，远大于最小安全距离50 m。因此，这4条协同航迹是满足时空安全性要求的。

假设导弹#1、#4的理想攻击角度分别为90°和30°，为了说明问题的简洁性，只为导弹#1、#4规划协同航迹，得到的航迹如图3-6所示。

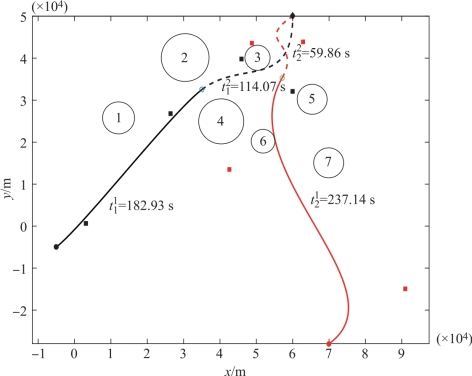
pagenumber_ebook=46,pagenumber_book=37

图3-6　导弹#1、#4的协同航迹

由图3-6可见，两枚导弹的第二段航迹存在交叉，交叉处τ1=0.773，τ2=0.319，则根据式（3-5）可算得从起点至交叉点的路程，进而算得两枚导弹在交叉处的飞行时间分别为266.9 s和258.64 s，可见两枚导弹并非同时到达航迹交叉处，导弹#4到达交叉处8.26 s后导弹#1才到达，因此所规划的航迹也是安全的。

需要说明的是，考虑到多导弹之间避免碰撞的问题，导弹发射位置应尽量选择散开的位置，对各导弹指定的理想攻击角度要和导弹的发射位置相对应（尽量避免图3-6所示的情况）。这种情况下，不安全航迹发生的可能性比较低。如果出现不安全航迹的情况，则可按照3.3.4节的方法对航迹进行重新规划。

协同航迹时空安全性判断与重生成

相关推荐