针对多飞行器协同任务规划问题，常用的模型有混合整数线性规划模型、多旅行商模型、多车辆路由模型、协同多任务规划模型等。通常采用直接法和间接法对航迹规划非线性最优控制问题进行求解，而采用基于几何学的搜索算法对航迹规划空间几何搜索问题进行求解。因此，相对单飞行器的航迹规划问题，多飞行器的协同航迹规划问题具有约束更多且更为复杂的特点。......
2023-08-02
多飞行器协同导控：限定攻击角度的航迹规划
【摘要】：在为某枚导弹进行航迹规划时，不必对集合中所有航迹节点进行考察。因此，本章提出导弹相关航迹节点集的概念。对于第k枚导弹，相关航迹节点集Wk的定义为：连接起点sk与目标e的线段与障碍分布德洛奈三角连接图所有相交边上的航迹节点构成的集合。以上述选点原则，设计第k枚导弹的航迹节点选取算法如下。此时，导弹k得到了一条能够避免威胁区并以指定攻击角度攻击目标的航迹。
将环境中的威胁区、禁飞区等不规则外形区域等效为一个半径为ro的圆区域，考虑安全余量rs＞0，每个威胁区的最小安全半径可定义为
假设导弹飞行的环境中有m个威胁区，其等效圆的圆心为Oj（j=1，2，…，m）、最小安全半径为rdj（j=1，2，…，m）。应用3.1.2节的德洛奈三角划分法连接威胁区等效圆的圆心，之后进行有效边的判定：如果两个圆心的连线不经过某个威胁区，则这条边为“有效边”，否则为“无效边”。将无效边从德洛奈三角划分法所构造的三角连接图中去除，并定义有效边在威胁区圆外部分的中点为导弹可经过的航迹点，由此得到除了起始点和目标点外导弹的其他航迹节点集合为
。
定义导弹经过此点的飞行方向单位矢量α满足
式中，
——当前航迹节点指向目标e的向量；
——由距离目标较远的威胁区圆心指向距离目标较近的威胁区圆心的向量，即满足
。
这样定义的飞行方向可使导弹垂直于障碍中心连线朝向目标飞行。
当飞行环境中存在多个障碍时，上述航迹节点集W包含较多元素。在为某枚导弹进行航迹规划时，不必对集合中所有航迹节点（特别是那些明显使导弹绕远的航迹节点）进行考察。因此，本章提出导弹相关航迹节点集的概念。
导弹相关航迹节点集：假设有N枚导弹，其起点分别为sk（k=1，2，…，N）。对于第k枚导弹，相关航迹节点集Wk的定义为：连接起点sk与目标e的线段与障碍分布德洛奈三角连接图所有相交边上的航迹节点构成的集合。
为降低航迹复杂性、提高规划速度，原则上，航迹所经过的节点数目越少越好。最好的情况为仅由一段从起点到达目标的贝塞尔曲线。因此，在设计航迹节点选取算法时，每次迭代均优先以目标为分段终点。若以目标为分段终点无满足约束条件的航迹，则应在导弹相关航迹节点集中选择距离目标较近的航迹节点为分段终点。以上述选点原则，设计第k枚导弹的航迹节点选取算法如下。
（1）将目标点加入导弹相关航迹节点集Wk，然后按照航迹节点距离目标距离
从小到大排列，目标点的
=0，因此在序列中目标点是第一个点。假设排好后的航迹节点序列为Wk′={P0，P1，P2，…，Pu，…，PM}，其中Pu表示按序排好后的第u个
的总个数，且P0=e。
（2）定义分段航迹的起点为S、终点为E，寻找可行点集Pick及不可行点集Ban。初始时，有S=sk、E=e、Pick={sk}、Ban=∅。考虑一般情况，针对起点为S、终点为E=Pu的一段航迹，采用式（3-11）中的模型对航迹进行优化，如果能够得到同时满足威胁区、过载、攻击角度等约束的优化解，则将Pu放入可行点集Pick。接下来，以Pu为分段起点，以P0=e为分段终点，再进行优化；如果不能够得到优化解，则取E=Pu+1，如果Pu+1出现以下任一情况，则舍弃Pu+1，继续取下一个值Pu+2进行判断，直至取到满足要求的点。
①出现在可行点集Pick中（意味着导弹已经经过该点）。
②出现在不可行点集Ban中（说明该点没有通往任何下一个点的可行航迹）。
③Pu+1的
值（说明Pu+1点与目标的距离大于分段起点与目标的距离，导弹将往回飞）。
以新取的点为终点E，再进行优化，综合以上考虑优化得到满足要求的航值大于S的
迹点。若直到W′k的最后一个点也不满足要求，则说明以S为起点没有可行的路径，因此，将其从Pick中删除，加入Ban。令新的起点S为此时可行点集Pick中的最后一个点，新的终点E指向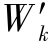
中的第一个点（即目标点），重新进行优化取点。
由初始化可知，第一步是以导弹的起点sk作为分段起点、目标点e作为分段终点，如果优化得到最优解，则说明导弹的航迹用一条贝塞尔曲线即可表征。否则，判断P1是否满足情况①、②、③，若不满足，就将P1作为分段终点进行优化，如果可得到优化问题的解，则
为得到的一段贝塞尔曲线航迹，接下来以P1为起点、目标点e为终点再进行优化，得到第二段贝塞尔曲线。如果将P1作为分段终点进行优化得不到解，则继续判断是否可将P2作为分段终点，照此类推。在优化过程中，如果出现前段有解而后段无解的情况（如sk至P2可得到优化解而P2至W′k中所有满足条件的点均无优化解），则将P2加入Ban，返回以sk为起点的过程，选择P3作为分段终点进行优化，如此往复。
（3）上述优化过程的终止条件：
①Ban={P1，P2，…，PM }，说明该任务无解；
②Pick中出现终点e，说明已经找到从导弹起点到终点的航迹，集合Pick就是得到的航迹节点集。此时，导弹k得到了一条能够避免威胁区并以指定攻击角度攻击目标的航迹。
有关多飞行器协同制导与控制的文章
- 详细阅读
-
多飞行器协同制导：攻击时间和角度约束制导律详细阅读
本章在此基础上，考虑攻击角度的约束，给出能够同时实现攻击时间约束和攻击角度约束的末制导律。因此，导弹在预测时采用三维制导律表达式为不同于文献[58]中通过纵向弹道的调整来实现攻击时间约束，本章通过在侧向制导指令中加入理想攻击时间与预测攻击时间的误差作为反馈项来实现对攻击时间的控制，而在纵向采用式所示的偏置比例导引律来实现对攻击落角的控制。......
2023-08-02
-
多飞行器协同制导：预测校正的攻击时间约束控制详细阅读
类似于8.3节中飞行后期的PNG切换，此时，最终导弹的整体飞行时间与要求的Td也不会相差太多。图8-5采用PITCG和PNG时4枚导弹的弹道对比由图8-5可知，在这两种制导律下，4枚导弹均命中了目标。4枚导弹采用PNG时的攻击时间分别为32.4 s、29.8 s、26.4 s和29.77 s，最大攻击时间差为6 s；当采用PITCG时，4枚导弹的攻击时间分别为35.06 s、35.02 s、35.07 s和34.97 s，导弹3的攻击时间与理想攻击时间的差最大为0.07 s，4枚导弹的最大攻击时间差为0.1 s。......
2023-08-02
-
多飞行器协同制导求解详细阅读
由于λ12包含x11和x12项，因此和不能由当前时刻的状态进行求解，需要求解x11和x12的表达式，将式代入式的第二个方程，并由t到tf进行积分，可得x12的表达式为式中，Φ1（·）——状态转移矩阵。通过求解式，可得x11和x12的表达式为将式代入式，可得x11和x12的最终表达式；将得到的x11和x12的表达式代入式，可得λ12的表达式；将λ12代入式，即可得到防御弹和目标加速度的闭环解。......
2023-08-02
-
德洛奈三角划分法-飞行器协同导控详细阅读
为在多障碍环境下确定导弹飞行的待选航迹节点，在此引入德洛奈三角划分法来确定导弹可能要飞经的边，以便为进一步设计搜索算法奠定基础。令J是点集P的一个三角划分，假设其含有m个三角形，将这m个三角形所包含的3m个角（α1，α2，…假设P是平面上的一个点集合，那么P的角度最优三角划分就是P的德洛奈三角划分。有关德洛奈三角划分的具体实现过程可参考文献[41]，这里不再详述。......
2023-08-02
-
导弹贝塞尔曲线航迹模型——多飞行器协同制导与详细阅读
假设导弹在二维平面的航迹为贝塞尔曲线，为了能够构造满足给定起点、终点以及攻击方向约束的航迹，本章采用三次贝塞尔曲线，即n=3。贝塞尔曲线航迹在起点与终点处的切线方向分别与向量一致，因此，可通过设置控制点b2来控制导弹攻击目标的方向。图3-1三次贝塞尔曲线控制点与曲线关系示意图图中，B（τ）为基于某4个控制点b0、b1、b2及b3的三次贝塞尔曲线航迹。......
2023-08-02
-
多飞行器协同制导控制方法详细阅读
此时，将式视为系数由t=t1时刻rmd、等量确定的线性定常系统，基于最优控制理论来设计协同制导律。由式和式可知，防御弹控制量wq与目标控制量vq的关系为由式和式可得哈密顿函数为式中，λ21和λ22为协态量，其正则方程分别为λ21和λ22在末端时刻满足的横截条件分别为式中，由式和式，可解得协态量λ21和λ22分别为式中，χ=/rmd≈-1。......
2023-08-02
-
多飞行器协同控制成果详细阅读
在预设性能控制理论中，通过合理设置性能函数，控制器可保证稳态时跟踪误差e收敛到一个预先设定的区域，且其瞬态性能同样满足预设的与性能函数相关的条件。图5-1跟踪误差与性能函数的关系曲线为了能够控制各飞行器在x、y、z三个方向的相对位置，将第一个子系统采用预设性能控制策略来进行设计。......
2023-08-02
相关推荐