基于Dubins路径协调的可飞行迹

2023-08-02 理论教育版权反馈

【摘要】：基于任务分配方案，结合上述Dubins路径协调方法，可得到完整的无人机可飞航迹。图2-10显示了通过Dubins路径协调得到的符合任务时序和最小转弯半径约束的7架无人机的可飞航迹。因此，如图2-10所示，u5采用Dubins曲线进行路径协调，中间绕路等待u7对T3实施完侦察识别后，其正好飞至T3，对T3实施攻击。

通过前述算法，可得到各无人机需完成的任务及时序。但是，由于无人机速度不同，故就有可能出现某速度较快的无人机到达某个目标后必须等待另一无人机完成任务后它才能开展任务的情况；另外，无人机的飞行需要满足其可用过载的约束。因此，本节在前述任务分配方案的基础上为每架无人机规划和协调一条满足任务时序约束和动力学约束的可飞航迹。

以无人机从目标T1至目标T2为例，中间的路程采用Dubins曲线，其中的圆弧段满足无人机最小转弯半径约束。在某些情况下，无人机在从目标T1至目标T2的过程中，需要等候一定的时间Δt，此段时间的轨迹采用两种方案——圆轨迹或侧向附加路径轨迹。如果等候时间Δt≥t*（t*为无人机按最小转弯半径圆周飞行的时间），则无人机按照一个或多个适当半径R（R大于等于最小转弯半径Rmin）的圆周做圆周运动；如果延迟时间Δt＜t*，则基本飞行路径将添加适当的侧向附加路径，如图2-7所示。

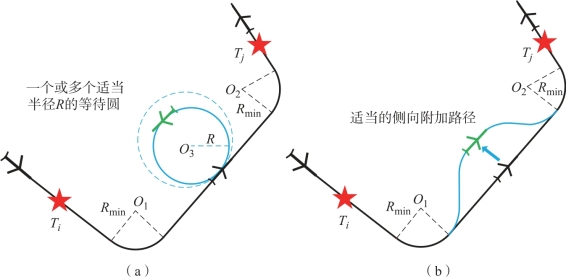
pagenumber_ebook=27,pagenumber_book=18

图2-7　路径协调示意图

（a）Δt≥t*；（b）Δt＜t*

图中，O1、O2和O3为圆弧段航迹的圆心。基于任务分配方案，结合上述Dubins路径协调方法，可得到完整的无人机可飞航迹。

例2-1　假设有7架无人机对5个目标完成侦察识别、攻击和毁伤评估任务，且无人机执行一个任务所需的时间为5 s。无人机和目标的具体信息见表2-2和表2-3。表中，x0、y0表示无人机的初始位置坐标，V、Rmin、Lmax分别为无人机的速度、最小转弯半径和最大航程。

表2-2　无人机信息

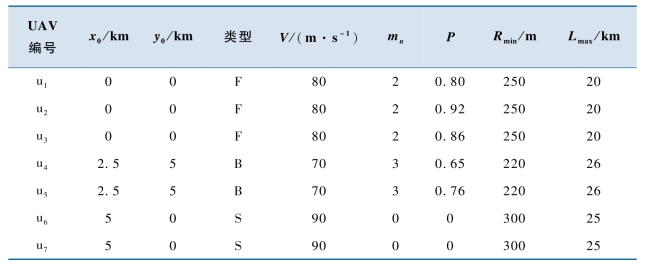
pagenumber_ebook=28,pagenumber_book=19

表2-3　目标信息

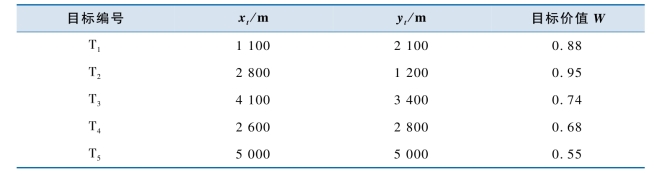
pagenumber_ebook=28,pagenumber_book=19

采用基于MGA的任务分配算法，得到的仿真结果如图2-8～图2-10所示。

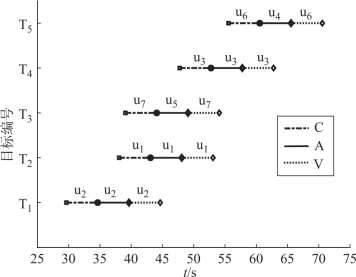
pagenumber_ebook=28,pagenumber_book=19

图2-8　各目标被侦察识别、攻击和毁伤评估的情况

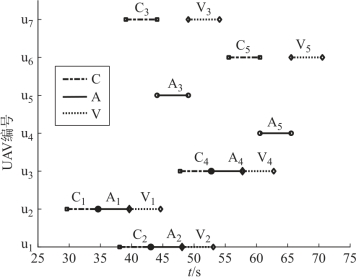
pagenumber_ebook=29,pagenumber_book=20

图2-9　各无人机的任务分配方案

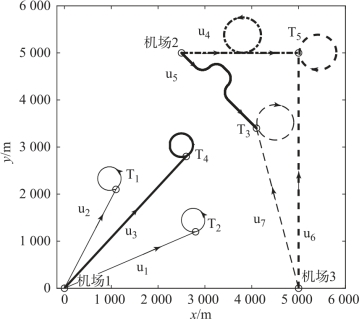
pagenumber_ebook=29,pagenumber_book=20

图2-10　基于Dubins路径协调的无人机航迹

由图可知，3种类型的7架无人机从3个机场出发，按照时序约束完成了对5个目标的协同侦察识别、攻击和毁伤评估任务，并在最短时间内获得了最大收益，且不存在“死锁”现象。由优化结果数据可知，异构多无人机群的最长飞行时间为71 s，最大攻击收益为3.1，最大性能指标函数为0.043。图2-10显示了通过Dubins路径协调得到的符合任务时序和最小转弯半径约束的7架无人机的可飞航迹。

接下来，以针对T3的侦察识别、攻击和毁伤评估为例来说明任务分配和路径协调情况。根据任务分配结果，u7和u5协同对T3进行侦察识别、攻击和毁伤评估。u5必须在u7对T3实施完侦察识别后，才能对其进行攻击。但是u5和u7同时起飞后，若其均直线飞至T3，则u5会先到达。因此，如图2-10所示，u5采用Dubins曲线进行路径协调，中间绕路等待u7对T3实施完侦察识别后，其正好飞至T3，对T3实施攻击。而在u5对T3实施攻击的过程中，u7在T3附近做圆周运动，等待u5完成攻击后对T3进行毁伤评估。多无人机对其他目标的任务执行情况可类似分析。

基于Dubins路径协调的可飞行迹

相关推荐