1.终端约束令t0、tf分别为编队形成段的初始时刻与末端时刻，为保证从弹在tf时刻到达指定编队位置，需对从弹在tf时刻的相对位置x、y、z进行约束：式中，x*，y*，z*——从弹在领弹弹道坐标系下的期望编队位置。......
2023-08-02
多飞行器任务规划约束条件
【摘要】：异构多无人机协同任务分配考虑的约束如下。
采用图论描述方法对多无人机协同任务分配问题进行描述，该方法将无人机可能的路径以一个有向图的方式表达出来，有向图的节点和边集为
式中，VT——目标集合；
VU——无人机的起始点集合；
V——有向图的节点集合；
E——有向图的边集，从V中的节点指向VT中的节点，表示所有可能的路径。
其中，k=1，2，3，分别对应于C、A、V。
异构多无人机协同任务分配考虑的约束如下。
（1）任务数量约束：保证目标的所有任务都被执行，可表示为
式中，NVT——V的势，NVT=‖V‖=NV+NT；
（2）路径约束：对无人机∀u∈VU来说，路径Pau是一条可飞的路径，即
（3）任务时序约束：对目标首先进行侦察，再进行打击，最后进行评估，可表示为
式中，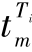
（m=C、A、V）——目标Ti被无人机执行相应任务时的时间。
（4）无人机机载弹药约束：设mu为无人机u（u∈VU）携带的最大弹药量，无人机攻击的目标数必须小于等于最大弹药数，因此约束可表示为
（5）航程约束：任意无人机u的飞行航程都小于其最大航程
，表示为
式中，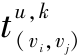
——无人机u沿着有向边（vi，vj）执行任务k的时间；
vu——无人机u的飞行速度。
有关多飞行器协同制导与控制的文章
- 详细阅读
-
多飞行器协同导控：限定攻击角度的航迹规划详细阅读
在为某枚导弹进行航迹规划时，不必对集合中所有航迹节点进行考察。因此，本章提出导弹相关航迹节点集的概念。对于第k枚导弹，相关航迹节点集Wk的定义为：连接起点sk与目标e的线段与障碍分布德洛奈三角连接图所有相交边上的航迹节点构成的集合。以上述选点原则，设计第k枚导弹的航迹节点选取算法如下。此时，导弹k得到了一条能够避免威胁区并以指定攻击角度攻击目标的航迹。......
2023-08-02
-
多飞行器协同制导求解详细阅读
由于λ12包含x11和x12项，因此和不能由当前时刻的状态进行求解，需要求解x11和x12的表达式，将式代入式的第二个方程，并由t到tf进行积分，可得x12的表达式为式中，Φ1（·）——状态转移矩阵。通过求解式，可得x11和x12的表达式为将式代入式，可得x11和x12的最终表达式；将得到的x11和x12的表达式代入式，可得λ12的表达式；将λ12代入式，即可得到防御弹和目标加速度的闭环解。......
2023-08-02
-
多飞行器协同导控技术详细阅读
针对多飞行器协同任务规划问题，常用的模型有混合整数线性规划模型、多旅行商模型、多车辆路由模型、协同多任务规划模型等。通常采用直接法和间接法对航迹规划非线性最优控制问题进行求解，而采用基于几何学的搜索算法对航迹规划空间几何搜索问题进行求解。因此，相对单飞行器的航迹规划问题，多飞行器的协同航迹规划问题具有约束更多且更为复杂的特点。......
2023-08-02
-
多飞行器协同制导控制方法详细阅读
此时，将式视为系数由t=t1时刻rmd、等量确定的线性定常系统，基于最优控制理论来设计协同制导律。由式和式可知，防御弹控制量wq与目标控制量vq的关系为由式和式可得哈密顿函数为式中，λ21和λ22为协态量，其正则方程分别为λ21和λ22在末端时刻满足的横截条件分别为式中，由式和式，可解得协态量λ21和λ22分别为式中，χ=/rmd≈-1。......
2023-08-02
-
多飞行器协同控制成果详细阅读
在预设性能控制理论中，通过合理设置性能函数，控制器可保证稳态时跟踪误差e收敛到一个预先设定的区域，且其瞬态性能同样满足预设的与性能函数相关的条件。图5-1跟踪误差与性能函数的关系曲线为了能够控制各飞行器在x、y、z三个方向的相对位置，将第一个子系统采用预设性能控制策略来进行设计。......
2023-08-02
-
多飞行器协同制导与防御弹2控制详细阅读
在目标、防御弹1和防御弹2协同对攻击弹拦截的过程中，目标和防御弹1采用式所示的协同拦截制导律飞行，防御弹2则跟踪防御弹1的弹目距离，最终实现和防御弹1同时拦截攻击弹。因此，当防御弹1与防御弹2距离攻击弹很近时，令防御弹2转为采用式所示的可实现落角约束的弹道成型制导律。......
2023-08-02
-
多飞行器协同避碰控制策略详细阅读
针对此问题，根据预设性能控制器可将系统误差控制在满足性能函数上下边界范围内的特点，可通过合理地设置性能指标函数来实现弹间的避碰。接下来，将上述性质应用于多弹编队成员间避碰策略的设计中。......
2023-08-02
相关推荐