首页理论教育固体火箭发动机设计：单向拉伸的极限状态

固体火箭发动机设计：单向拉伸的极限状态

2025-09-29 理论教育版权反馈

【摘要】：图3.29单向拉伸应力-应变曲线可见，常用σ-ε曲线在应力达到最大值后就下降，而真实应力-应变σ′-ε′曲线则是一条单调上升的曲线，一直到试件被拉断为止。F为最大值时的状态，称为单向拉伸的极限状态。将式微分，并代入式得上式表明，单向拉伸时，极限状态下的真实应变恰好等于材料的应变硬化指数n。于是，由式和式得若已知材料的屈服极限σ0.2和强度极限σb，则可根据式求出应变硬化指数n。

假设材料是各向同性、均质和无裂纹的。单向拉伸常用的应力和应变表达式分别为

pagenumber_ebook=159,pagenumber_book=150

式中　A0，L0——试件的初始横截面积和原标长；

　　　A，L——试件受力后的横截面积和标长。

这种常用的应力和应变表达式在大变形的情况下是不真实的。因为在拉伸过程中，试件逐渐变细，甚至出现缩颈现象。用拉伸力F除以试件的初始横截面积A0所得的应力σ，较试件所受的真实应力σ′要低得多。真实应变ε′和ε也不一样。

真实应力σ′和真实应变ε′定义为

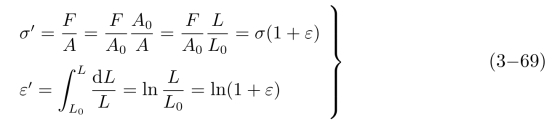
pagenumber_ebook=159,pagenumber_book=150

常用应力-应变（σ-ε）曲线和真实应力-应变（σ′-ε′）曲线的比较如图3.29所示。

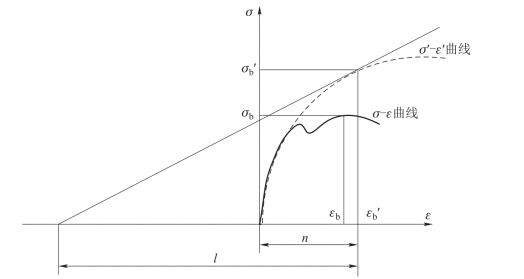
pagenumber_ebook=159,pagenumber_book=150

图3.29　单向拉伸应力-应变曲线

可见，常用σ-ε曲线在应力达到最大值（即强度极限σb）后就下降，而真实应力-应变σ′-ε′曲线则是一条单调上升的曲线，一直到试件被拉断为止。

通常σ′-ε′关系用幂函数来表达：

式中　n——应变硬化指数，对于理想塑性材料，n=0，对于一般金属材料，n＞0；

　　　 pagenumber_ebook=159,pagenumber_book=150 ——强度系数。

单向拉伸时，拉伸力为

在单向拉伸过程中，一方面由于应变硬化而使σ′上升，另一方面又使横截面积A不断减小。在拉伸开始后不久，σ′的增大量比A的减小量大，故F不断增大；但当拉伸变形到一定量以后，A的减小量会比σ′的增大量大，此时σ′开始减小。由此可知，F必有一最大值存在。F为最大值时的状态，称为单向拉伸的极限状态。此时

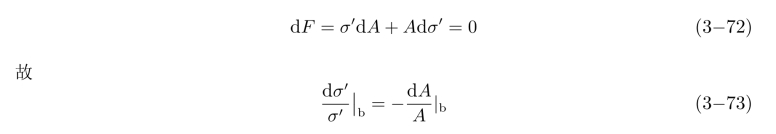pagenumber_ebook=160,pagenumber_book=151 (https://www.chuimin.cn)

假设塑性变形时，试件体积保持不变。亦即

pagenumber_ebook=160,pagenumber_book=151

由式（3-69）知，dε′=dL/L，故得

pagenumber_ebook=160,pagenumber_book=151

将式（3-75）代入式（3-73）得，在极限状态下，有

pagenumber_ebook=160,pagenumber_book=151

式（3-76）表明，单向拉伸时，极限状态下的真实应力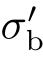 pagenumber_ebook=160,pagenumber_book=151 恰好等于真实应力-应变曲线在该点的切线的斜率，如图3.29所示。

将式（3-70）微分，并代入式（3-76）得

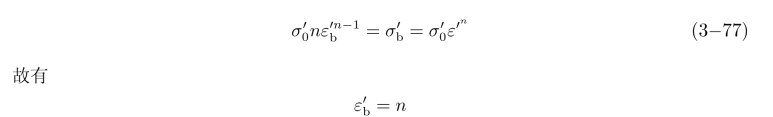
pagenumber_ebook=160,pagenumber_book=151

上式表明，单向拉伸时，极限状态下的真实应变 pagenumber_ebook=160,pagenumber_book=151 恰好等于材料的应变硬化指数n。

将上式代入式（3-70）得

同时，由式（3-69）和式（3-78）得

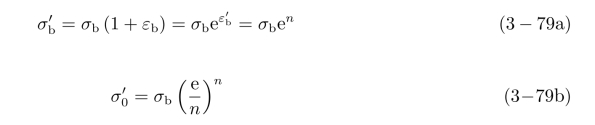
pagenumber_ebook=160,pagenumber_book=151

上式表明，材料的强度系数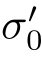 pagenumber_ebook=161,pagenumber_book=152 与其强度极限σb和应变硬化指数n有关。n的求法如下：

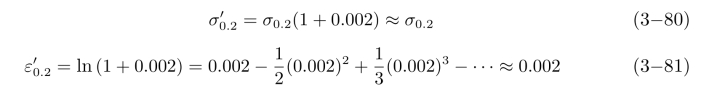
pagenumber_ebook=161,pagenumber_book=152

式（3-80）、式（3-81）中的σ0.2、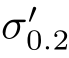 pagenumber_ebook=161,pagenumber_book=152 和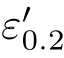分别代表材料产生0.2%永久变形时（屈服状态）的常用应力、真实应力和真实应变值。于是，由式（3-70）和式（3-79）得

pagenumber_ebook=161,pagenumber_book=152

若已知材料的屈服极限σ0.2和强度极限σb，则可根据式（3-82）求出应变硬化指数n。然后，再根据式（3-79b）求出强度系数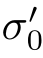 pagenumber_ebook=161,pagenumber_book=152 。这样，表征真实应力-应变关系的式（3-70）也就完全确定了。