阳光下的影子：五年级上册小学科学学习好帮手

2023-07-31 理论教育版权反馈

【摘要】：A.早晨B.正午C.傍晚D.都有可能2.一天中，我们生活的地方，阳光下物体的影子变化的规律是（）。A.北面B.东面C.南面D.西面7.小刚在上午11点和下午4点在同一地点对自己在阳光下的影子进行研究，以下结论中最有可能的是（）。第二天，小明同学从早上8点到下午4点，每个整点观测阳光下筷子的影子，所画的方向和长度图如图所示。

学生观察动画展示的圆变化成椭圆的过程，从宏观上发现圆上的点的横坐标不变，纵坐标通过压缩形成椭圆，然后通过思考，发现圆变化为椭圆，从本质上是坐标变换 pagenumber_ebook=201,pagenumber_book=194

此环节目的是让学生通过复习圆与椭圆的关系，发现坐标之间的关系，为下面借用圆的参数来表达椭圆的参数方程埋下伏笔，也是为了培养学生学会联系、学会分析的能力.

问题2：圆x2＋y2＝a2（a＞0）的参数方程是什么？既然圆可以通过上述变换得到椭圆，那你能否利用圆x2＋y2＝a2（a＞0）的参数方程，并借助上述变换得到椭圆 pagenumber_ebook=201,pagenumber_book=194 0）的参数方程？

1.一天中，阳光下物体的影子（　）最短。

A.早晨　B.正午　C.傍晚　D.都有可能

2.一天中，我们生活的地方，阳光下物体的影子变化的规律是（　）。

A.从西到东，从长到短到长　B.从东到西，从短到长到短

C.从东到西，从长到短到长　D.从南到北，从长到短到长

3.小丁中午站在阳光下，发现自己的影子在身体的前方，那么他朝（　）站着。

A.东　B.南　C.西　D.北

4.小丁同学在同一时间观察操场上的旗杆和自己的影子，关于这两个影子的情况，以下表述正确的是（　）。

A.方向相同，长短相同　B.方向不同，长短相同

C.方向相同，长短不同　D.方向和长短都不同

5.如图，夜晚，小刚朝前走将经过一个路灯，他影子的方向变化将会是（　）。

1.一天中，阳光下物体的影子（　）最短。

A.早晨　B.正午　C.傍晚　D.都有可能

2.一天中，我们生活的地方，阳光下物体的影子变化的规律是（　）。

A.从西到东，从长到短到长　B.从东到西，从短到长到短

C.从东到西，从长到短到长　D.从南到北，从长到短到长

3.小丁中午站在阳光下，发现自己的影子在身体的前方，那么他朝（　）站着。

A.东　B.南　C.西　D.北

4.小丁同学在同一时间观察操场上的旗杆和自己的影子，关于这两个影子的情况，以下表述正确的是（　）。

A.方向相同，长短相同　B.方向不同，长短相同

C.方向相同，长短不同　D.方向和长短都不同

5.如图，夜晚，小刚朝前走将经过一个路灯，他影子的方向变化将会是（　）。

A.前—后—前　B.后—下—前　C.后—前—后　D.前—下—后

6.傍晚，物体的影子的方向都朝着（　）。

A.北面　B.东面　C.南面　D.西面

7.小刚在上午11点和下午4点在同一地点对自己在阳光下的影子进行研究，以下结论中最有可能的是（　）。

A.长度和方向都相同　B.长度和方向都不同

C.长度不同，方向相同　D.长度相同，方向不同

A.前—后—前　B.后—下—前　C.后—前—后　D.前—下—后

6.傍晚，物体的影子的方向都朝着（　）。

A.北面　B.东面　C.南面　D.西面

7.小刚在上午11点和下午4点在同一地点对自己在阳光下的影子进行研究，以下结论中最有可能的是（　）。

A.长度和方向都相同　B.长度和方向都不同

C.长度不同，方向相同　D.长度相同，方向不同

1.设计与分析。

某个星期六，天气晴朗。小明用一根20厘米长的筷子、一块平滑的木板、一张白纸，做了一个简易的日影观测仪。右图是根据测得的数据绘制出的筷子影长变化折线图。

1.设计与分析。

（1）从图中可知，小明是从（　）时候开始做这个实验的。

A.上午　B.中午　C.下午　D.都有可能

（2）从图中可以看出，在这段时间里，筷子影长的变化规律是（　）。

A.随时间推移，筷子影子逐渐变长　B.随时间推移，筷子影子逐渐变短

C.随时间推移，筷子影子先变长再变短　C.随时间推移，筷子影子先变短再变长

（3）当这个实验继续进行半个小时，影子不可能出现的情况是（　）。

A.先变短后变长　B.逐渐变短　C.逐渐变长　D.完全消失

（4）如果小明从早晨到傍晚每半小时观测一次，那么筷子影子最短是在（　）。

A.早晨　B.中午　C.傍晚　D.都有可能

（5）为了提高实验观测的准确性，下列做法错误的是（　）。

A.用橡皮泥把筷子垂直固定在木板上

B.把日影观测仪放在始终能照到阳光的地方

C.记录时不能让底座移动

D.不断调整木板角度使影子始终落在白纸内

2.观察与讨论。

第二天，小明同学从早上8点到下午4点，每个整点观测阳光下筷子的影子，所画的方向和长度图如图所示。请看图回答问题：

（1）在阳光下，筷子影子最长是在（　）。

A.8点和16点

B.9点和15点

C.10点和14点

（1）从图中可知，小明是从（　）时候开始做这个实验的。

A.上午　B.中午　C.下午　D.都有可能

（2）从图中可以看出，在这段时间里，筷子影长的变化规律是（　）。

A.随时间推移，筷子影子逐渐变长　B.随时间推移，筷子影子逐渐变短

C.随时间推移，筷子影子先变长再变短　C.随时间推移，筷子影子先变短再变长

（3）当这个实验继续进行半个小时，影子不可能出现的情况是（　）。

A.先变短后变长　B.逐渐变短　C.逐渐变长　D.完全消失

（4）如果小明从早晨到傍晚每半小时观测一次，那么筷子影子最短是在（　）。

A.早晨　B.中午　C.傍晚　D.都有可能

（5）为了提高实验观测的准确性，下列做法错误的是（　）。

A.用橡皮泥把筷子垂直固定在木板上

B.把日影观测仪放在始终能照到阳光的地方

C.记录时不能让底座移动

D.不断调整木板角度使影子始终落在白纸内

2.观察与讨论。

第二天，小明同学从早上8点到下午4点，每个整点观测阳光下筷子的影子，所画的方向和长度图如图所示。请看图回答问题：

（1）在阳光下，筷子影子最长是在（　）。

A.8点和16点

B.9点和15点

C.10点和14点

通过这种坐标变换的关系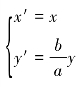 pagenumber_ebook=201,pagenumber_book=194 ，联系圆的参数方程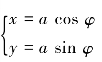，得到椭圆的参数方程

从问题1到问题2，过渡自然，学生顺利地接受了椭圆参数的选取过程，通过问题2的过渡，很容易回答下面的问题3，从而破解本节课的难点.

问题3：椭圆参数方程中的参数φ的几何意义是什么？

通过上面的铺垫，学生解决问题3很容易，但是为了让学生深刻地认识参数φ的意义，所以让学生看椭圆随着圆变化而形成的动画过程，此时显示的过程是通过坐标变换引起的，学生可以清晰地认识到椭圆中φ不是旋转角，而是离心角.

为了进一步使学生对椭圆参数方程有更全面的认识，教师设计了这样的课堂追问：

追问1：φ是不是OM的旋转角？

追问2：φ与∠xOM在A点转动一周的过程中有相等的可能吗？如果有可能，有多少次？

追问3：实际上φ与∠xOM之间有一个等式关系，请大家尝试找到这个等式关系.

追问4：你觉得椭圆的短半轴b是图形中的哪条线段？

通过4个追问，强化了学生掌握∠xOM与φ的区别和联系，同时发现φ与∠xOM在坐标轴上是相等的，它们之间还有关系：tanφ＝tan∠xOM，其中，半径为b的小圆也凸显出来，和教材紧扣，克服了教材直接生硬的感觉.

阳光下的影子：五年级上册小学科学学习好帮手

相关推荐