1.任意角的三角函数的定义在本章的2.2节已经讨论了锐角的三角函数值,但是把角的概念推广以后,角可以为任意大小,那么对于任意角α,又该如何确定其三角函数值呢?......
2023-11-22
数学组 王鹏飞
学习目标
1.(1)掌握任意角的正弦、余弦、正切的定义;(2)掌握正弦、余弦、正切函数的函数值的求解;(3)正确理解三角函数是以角为自变量的函数.
2.在任意角三角函数概念的形成过程中,提高分析、探究、解决问题的能力,培养学生的直观想象能力,体会函数思想,培养学生抽象思维能力,体会数形结合思想.
3.(1)使学生认识到事物之间是有联系的,三角函数就是角度(自变量)与比值(函数值)的一种联系方式,加强学生逻辑推理能力培养;(2)学习转化的思想,培养严谨治学、一丝不苟的科学精神.
重点难点
1.任意角的正弦、余弦、正切的定义.
2.任意角的三角函数概念的建构过程.
学习探究
问题1:如图1所示的是我们儿时的玩具——风车,在它的一圈一圈转动的形式背后,也蕴含了丰富的数学内涵(如周期性).下面先看一个具体的数学问题:
图1
图2
(1)如图2所示,半径为1的风车中心O到平面的距离h=2,点P到点O在同一水平线上,当点P逆时针旋转α时,点P离平面的距离H是多少?比如,![]() 时,H=________?
时,H=________?
(2)那么当![]() 时,还可以用H=r sinα+h进行计算吗?如果可以,
时,还可以用H=r sinα+h进行计算吗?如果可以,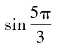 又是多少?
又是多少?
为了解决这类问题,下面我们一起进入今天研究的课题——“任意角三角函数的定义”.
【设计理由】用生活中常见的玩具——风车,学生儿时都有所接触,较为熟悉,再将此转化成一个数学问题,在理科教学中可以增加趣味性,让学生集中注意力尽快进入上课状态,任意角的三角函数是从圆周运动中发展而来的,与此同时引出周期现象,三角函数是研究周期性的一个重要函数,让学生对三角函数的这一特性有一个初步了解,同时也引发学生的认知冲突,让学生初步了解本节课学习的任务,激发学生学习新知的兴趣和欲望,培养学生直观想象、抽象思维能力.
【使用说明】教师提出问题,学生独立完成,当学生完成问题1中(2)小问时会遇到困难,此时暂时不去解决,引出课题.
问题2:如图3所示,初中是如何在直角三角形中定义锐角三角函数的?
【设计理由】回顾初中的锐角三角函数的定义,为后面在坐标系中重新定义三角函数作铺垫,从原有的认知基础出发,认识任意角的三角函数的定义.
图3
图4
问题3:如图4所示,前面已经在直角坐标系中研究了任意角,你能否用直角坐标系中角的终边上的点的坐标表示锐角三角函数?
【设计理由】角是在坐标系中重新定义的,因此三角函数也需要在坐标系中重新定义,引导学生用坐标法来研究锐角三角函数,让学生初步抽象出三角函数的定义.
【使用说明】学生自主预习教材,思考并完成问题2、问题3.
问题4:如图5所示,当角α确定,三角函数比值会随着P点在角α的终边上位置的改变而改变吗?为什么?
图5
【设计理由】取OP=1,体现简约思想,并且OP=1会使P点在半径为1的圆上运动,顺势提出单位圆概念.
【使用说明】使用几何画板动画展示,在单位圆上拖动P点,锐角α改变,P点的坐标也在发生改变,观察比值是否发生改变,验证学生的结论.
问题5:如图6,在单位圆中,P点在圆周上运动,观察发现P点的坐标、坐标比会随着角α的变化而变化,P点的坐标或坐标比和角α之间有什么关系?请以锐角为例进行说明.
图6
【设计理由】前面为此处做了很多铺垫,这时候让锐角α动起来,让学生观察感受函数的动态特点,有利于学生探究、理清此处的函数关系,再探究单位圆上的表达式,反复巩固单位圆上的定义,为提出任意角三角函数的定义做铺垫,并再次强调P点是单位圆上的点,本质是在强调我们对三角函数的定义,后面都是在单位圆上进行的.
【使用说明】教师提出,这个P点是任意的一点吗?强调是角α终边与单位圆的交点.
问题6:当角α是任意角时,这些还成立吗?它们还是函数关系吗?(动画展示角α是任意角时,观察P点的坐标变化).
【设计理由】由于学生对任意角三角函数的定义的认识是重难点,并且教材中对这块的处理是先提出任意角三角函数的定义,再去说明对于确定的角α,三个值都唯一确定来说明函数,此处运用几何画板动画观察,先让学生观察发现P点横纵坐标、坐标比值随着角α的变化而变化,并且唯一确定,先让学生体会这是函数,再顺理成章地提出这个函数称为三角函数,处理更为自然。在此可以先主要观察从锐角的正弦定义推广到任意角的正弦定义,先解决一个,再运用类比思想提出并探究余弦、正切,突破难点,从而达到从锐角三角函数定义推广到任意角三角函数的定义,突破重难点.
【使用说明】在此,教师提出任意角三角函数定义:
如图5,设α是一个任意角,它的终边与单位圆交于点P(x,y),那么:
(1)y称为α的正弦(sine),记作sinα,即sinα=y;
(2)x称为α的余弦(cossine),记作cosα,即cosα=x;
(3)![]() 称为α的正切(tangent),记作tanα,即tan
称为α的正切(tangent),记作tanα,即tan![]() .
.
正弦、余弦、正切都是以角为自变量,以单位圆上点的坐标或坐标的比值为函数值的函数,我们将它们统称为三角函数.
【反馈练习】
例1 求![]() 的正弦、余弦和正切值.
的正弦、余弦和正切值.
例2 已知角α的终边经过点P0(-3,-4),求角α的正弦、余弦和正切值.
【设计理由】例1解决初始问题,例2使学生认识到,只要知道角的终边上的任意一点,就可以得出相应的三角函数值,通过例题进一步加深对定义的理解.
【使用说明】学生独立完成,教师引导、评价,关注学生解题中遇到的问题.
达株检测
1.一般地,设任意角α终边上任意一点的坐标为P(x,y),它与原点的距离为r,则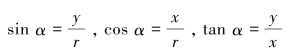 ,你能自己给出证明吗?
,你能自己给出证明吗?
2.已知角α的终边经过点PO(-3t,-4t),求角α的正弦、余弦和正切值.
3.观察发现,角终边在不同象限时,其三角函数值符号不同,有没有什么规律?
【设计理由】加强课后练习与巩固,且思考题1突出了点P的任意性,说明任意角α的三角函数值只与α有关,而与点P在角的终边上的位置无关,思考题2是对例2的进一步深入,思考题3对定义的进一步巩固,并了解三角函数值上的一个简单特点.
【使用说明】根据学生情况选择使用,酌情删减或增加.
有关天高地阔,凤举鸾翔 重庆市凤鸣山中学基于核心素养的课程改革探索与实践的文章

1.任意角的三角函数的定义在本章的2.2节已经讨论了锐角的三角函数值,但是把角的概念推广以后,角可以为任意大小,那么对于任意角α,又该如何确定其三角函数值呢?......
2023-11-22

重点难点1.物质的量在化学方程式计算中的应用。初步学会物质的量在化学方程式计算中的应用和初步学习化学反应中转移电子物质的量的计算。求该钠块中未被氧化的钠及Na2O2的物质的量。......
2023-07-31

政治组李红学习目标1.识记我国分配制度的内容;理解按劳分配的内容、必要性,生产要素按贡献参与分配的意义;区分现实生活中不同的分配方式,分析个人家庭收入的来源。因而在按劳分配中不能提“不劳不得”。教师要进行点拨式教学,帮助学生在教师所提问题基础上进一步质疑,发现并提出问题。让学生彻底明白各种分配方式,特别是对按劳分配、按劳动成果分配和按生产要素分配三者的区分。......
2023-07-31

生物组王若愚学习目标1.说出内环境的概念和组成。由肠道吸收的脂肪大部分是由小肠绒毛的毛细淋巴管吸收。写出下表中细胞生活的内环境名称。最后一个表格,是易错点,再次重复内环境的概念以及内环境所包含的组分。学生结合实际例子,通过互动、展学和评价纠错,能够更深入地理解内环境是细胞与外界进行物质交换的媒介这一事实。......
2023-07-31

数学组聂晓红学习目标1.理解三角形的三边关系,能用三角形的三边关系解决相关问题。重点难点1.三角形三边关系的探索和应用。分别去尝试摆三角形。进一步达成目标1和目标3。这两道题是对三角形三边关系的灵活运用,通过学习反馈,了解学习效果,进一步达成目标1。培养学生“用数学”的意识。达株检测★1.以下列各组线段为边,能组成三角形的是()。......
2023-07-31

英语组周聪学习目标1.Learn the step of writing a thank-you note.2.Learn to speak gratitude out to people who have helped you.重点难点1.Use advanced sentences to write a thank-you note.2.Find the structure of writing a thank-you note.学习探究问题1:What have you done for your mother?Read a poem related to a thank-you note.引入话题,朗读诗歌,在诗歌中感受“感恩”的氛围。问题3:Can you find the steps of writing a thank-you note?Summarize the basic structure of a thank-you note.Dear Mom,How is everything going?......
2023-07-31

数学与三角函数是指通过数学和三角函数进行简单的计算,例如对数字取整、计算单元格区域中的数值综合或其他复杂计算。常用的数学与三角函数包括INT、ROUND、SUM、SUMIF等函数。在制作成绩统计表之前,需要先了解一些简单的常用函数。图6-52填充后的效果◆知识链接其他数学与三角函数简介:条件求和函数SUMIF主要功能:对指定单元格区域中符合一个条件的单元格求和。......
2023-11-23

化学组孟娅娅学习目标1.了解元素周期表的发展历程。重点难点元素周期表的编排规则及结构,元素在周期表中的位置。通过问题1进一步熟悉元素周期表的结构,提醒学生注意特殊位置结构。结合元素周期表找规律,并回答问题。这节课内容主要是让学生了解并熟悉元素周期表的结构和规律,在此基础上对思维进行提升。......
2023-07-31
相关推荐