（一）学前儿童时间概念的教育内容与要求1.小班初步理解与运用早上、中午、晚上、白天、夜晚等时间词语。（二）学前儿童货币概念的教育内容与要求1.中班初步了解货币的价值和作用。能进行简单的人民币的兑换，能进行1元与1角（或5角）的换算活动，以及10元与1元（或5元）的换算活动。能参与简单的购物活动。养成爱护人民币，节约用钱的好习惯。思考与练习常见的幼儿货币概念的教学方法有哪些？......
2023-07-30
学前儿童数学教育：集合概念的发展与教育要求
【摘要】：（一）集合的概念集合是指具有某种共同属性的事物的全体。放在一起归为交通工具一类，称为交通工具的集合。集合的表示法有列举法、描述法、文氏图法。（三）幼儿集合的发展阶段与特点苏联儿童数学教育家A.M.列乌申娜的《学前儿童初步数概念的形成》指出了不同的年龄时期幼儿的集合概念的主要特征和表现。在3岁前，婴幼儿的集合的概念发展是比较笼统、泛化的阶段。
（一）集合的概念
集合是指具有某种共同属性的事物的全体。在我们的生活中，往往把相同类的事物归为一类，如公交车、小汽车、大卡车、三轮车……放在一起归为交通工具一类，称为交通工具的集合。幼儿在经验不断丰富的过程中，认识世界的事物，为了获得事物的名称，往往在脑海中会创造或者形成一些集合，比如获得“猫”的集合，那么他则会想到自己家的猫、别人家的猫、流浪的猫等，进而给“猫”下一个定义，形成“猫”的集合的概念。
（1）集合的表示法有列举法、描述法、文氏图法。①列举法即把集合中的每一个元素一一写在大括号里，如{苹果、橘子、香蕉}。②描述法即把具有同一特征的元素用语言描述的形式写出来，如{10以内的自然数}。③文氏图法即用一个封闭的图形象征地把元素包围起来表示集合，如图4-1。
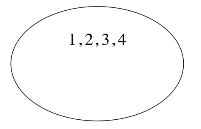
图4-1 文氏图法
（2）集合中的元素具有确定性、互异性、无序性的特点。即一个集合中的具有同一特征的元素是确定的，并且是单一的，没有顺序的。
思考与练习
从集合的角度，用集合的方式把加法、减法呈现出来。
答案解析：从集合方面来看，幼儿数学中的加法就是求已知两个没有公共元素的有限集合的并集的基数，减法就是求有限集合与它的子集的差集的基数，因此，集合概念就是幼儿掌握数概念，进行数运算的基础。
（二）发展幼儿集合概念的意义
集合是数学中的一个基础概念，是幼儿学习数学的基础。学前期是幼儿启蒙数学教育的重要时期，在这个时期幼儿获得集合的经验对幼儿形成严密的数学逻辑，积累相应的感性经验意义重大，应该引起足够的重视。
1.集合是幼儿形成、掌握数概念和计数准备的基础
用数字描述来表述一个集合有“多少”物体是一个非常重要的内容，[2]即可以用具体的数字来表述集合的元素的数量。例如，让幼儿指出某一箩筐里有多少橘子，那么幼儿首先需要知道哪些水果是橘子，哪些不是，把橘子和其他的水果区分出来之后，再来数一数橘子的数量。这就表明，幼儿数数是在对集合属性认识的基础上进行的。幼儿的数学教学不是从数词的计算开始的，而是先从笼统的感知集合、比较集合、建立集合概念的基础上开始的。在幼儿数学教育的启蒙阶段，集合和集合中的一一对应的概念是帮助幼儿认识周围的世界，形成数学思维的基础，是进一步学习数学的基础，如图4-2。在幼儿数学启蒙或者日常教育中，一一对应的思想会时刻渗透在他们计数之时。
图4-2 一一对应思想的应用
2.学习集合有利于学前儿童发现事物的共同属性
幼儿不断丰富自我集合经验的过程，就是幼儿发现事物间的共同属性的过程，如发现几何图形的颜色、形状属性。若是幼儿在感知集合的过程中，能从相同数量的事物中发现事物的等数性，那么意味着幼儿向抽象出数的阶段又更进了一步，有利于幼儿概括出数的概念。
3.感知集合是学前儿童理解数的组成和数的运算的前提条件
集合有着本身的独有特点，集合与集合之间存在着交集、并集、差集、补集等运算关系。学前儿童在数学启蒙阶段若是能够很好地丰富自身的集合经验，那将会为以后学习数的组成和数运算打下坚实的基础。如数4可以分成1和3、2和2，这组数的组成可以看成集合与子集之间的关系。同样的4是由1和3或者2和2组成的，同样可以看成集合的两个子集的合集等同于加法运算，减法即是集合与子集之间的运算关系。感知集合是让幼儿从包含关系、整体与部分的关系角度来进行数的运算，这是后期幼儿数运算的基础前提。
（三）幼儿集合的发展阶段与特点
苏联儿童数学教育家A.M.列乌申娜的《学前儿童初步数概念的形成》指出了不同的年龄时期幼儿的集合概念的主要特征和表现。具体如下：
1.3岁前笼统感知、泛化阶段
婴幼儿数概念的发生经历了辨数—认数—点数的发展规律。1984年杭州师范学院（现杭州师范大学）吕静和王伟红的《婴幼儿数概念的发生的研究》中详细地展现了：2～5岁儿童的辨数（能辨别出两堆不同数目物体的多少）、认数（瞬时内不凭数数，只凭直觉说出物体数目）和点数（能逐一按物数数，并说出总数）[3]。在3岁前，婴幼儿的集合的概念发展是比较笼统、泛化的阶段。具体体现在：①感知的集合是没有界限的；②没有感知到集合中元素的具体数目。比如：让一个3岁前的婴幼儿去把散落在地上的10个苹果捡起来，在他捡起了3或4个苹果以后，你问他：“宝贝，捡完了所有的苹果吗？”他会回你：“捡好了所有的苹果。”这表明该阶段的幼儿还没有感知集合中的元素。
思考与练习
纽扣示范图1
幼儿摆放图2
上图1是教师给的示范图，按照图1，幼儿摆放出图2的样子，说明幼儿摆放不是把空隙填满，而是会不断超出规定的界限，这说明3岁前的婴幼儿对集合没有明确的边界的意识。
2.3～3.5岁前期能感知到有限的集合
该年龄阶段的幼儿开始对集合的边界有了一定的意识，在做集合的活动时，能够有意识地注意边界问题，同时该阶段的幼儿往往把注意力集中在集合的边界上，而不会感知到集合中的元素及数量，换言之，其对集合的数量构成的感知是泛化、笼统的，不精确的。另外，儿童感知统一完整的集合时，往往有两个边界起算点。
例1：
图4-3 示范图
图4-4 幼儿摆放图
在例1中，教师给出示范图4-3，3岁左右的幼儿，按照示范图摆放出图4-4，一般是把两边先摆放好（意识到了集合的边界），之后再把中间的空隙填满，这时候往往数量上是与示范图不相符合的，这也说明此阶段的幼儿有了集合边界的意识，但是对于集合元素的构成还没有精确的意识。
例2
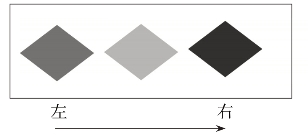
图4-5 左边界起点
图4-6 右边界起点
在例2图4-5中，当幼儿从集合的左边的边界开始摆放物品时，一般遵循从左到右的顺序摆放；图4-6中，当幼儿从集合的右边界为起点摆放物品时，一般遵循从右到左的顺序摆放。
3.3.5～6岁感知集合元素构成，进行简单的集合运算
该阶段若是幼儿经过了必要的数学启蒙，从3.5岁始，能采用一一对应的方式来比较两个集合的等量关系，4岁左右开始对集合元素精确感知。5岁幼儿对集合的理解更加灵活，能知道集合可由不同性质的元素组成，能用计数的方法比较两个集合元素的相等、多、少。6岁幼儿已能学会集合的简单运算。[4]
（四）集合与分类的关系
集合与分类是数学概念中关系比较密切的两个概念。分类是指对一组事物按照一定的标准加以区分，并进行归类的过程。分类是一种认知的能力，是在幼儿观察和比较之后必然进行的思维过程，贯穿幼儿认识周围世界的全过程。分类是儿童对集合进行区分的过程，是集合思想的体现。集合是分类活动的基础，对集合的区分和合并被称为分类。[5]分类也是逻辑思维的一个重要组成部分。在日常的生活中，幼儿会接触到事物的不同种类、颜色、大小，他们首先需要对其进行属性的区分，然后分类成不同的集合，方能进行数数和计数。幼儿集合与分类经验不断形成和丰富的过程也正是帮助其建构有关数概念的基础。根据幼儿的年龄不同分类具有各个年龄阶段的认知特点，分类根据不同的标准有不同的分类。在幼儿的数学启蒙教育中，幼儿进行相关的活动主要不是为了认识事物的属性，而是为了让学前儿童在认识事物属性的过程中，不断认知到分类的过程和明白集合是怎样形成的，最终获得应有的数学思维，为以后数学的学习打下基础。
有关学前儿童数学教育的文章
- 详细阅读
-
学前儿童空间方位概念的发展与教育-第10章-详细阅读
小芳老师是刚刚参加工作的新老师，在某幼儿园小班做配班老师。这时，音乐响起，小芳老师精神抖擞面对面地站在了孩子的前面。这表明小班幼儿在认识空间方位时，不能从客体为中心的角度辨别空间方位，小班幼儿并不知道小芳老师的左边是他们的右边。......
2023-07-30
-
学前儿童数学教育的教学内容与要求详细阅读
（一）学前儿童量概念的教育内容与要求通过有目的、有计划的教育使学前儿童认识和掌握量的概念，量的概念对幼儿数概念和思维能力的发展有着重要的作用。（二）学前儿童模式概念的教育内容与要求在学前儿童数学启蒙教育中，模式的识别和运用能力的培养是促进儿童数学认知发展和逻辑思维能力发展的重要方面，其具体的教学内容主要包括对重复性模式的识别、复制、扩展、创造、比较、描述和交流等。......
2023-07-30
- 详细阅读
-
学前儿童数学教育：几何形体概念的发展与教育详细阅读
幼儿已经初步认识了三角形，陈老师为巩固幼儿对三角形的认识，更好地掌握三角形的特征，组织设计了一次数学活动：寻找三角形。陈老师对幼儿说：“请小朋友们找出你们认为是三角形的图形来。”陈老师话音刚落，小朋友们就开始摆弄桌上的图形了。......
2023-07-30
- 详细阅读
-
学前儿童数学教育的目标体系详细阅读
（一）学前儿童数学教育的总目标对周围环境中事物的数量、形状、时间和空间等感兴趣，有好奇心和求知欲，喜欢参加数学活动和游戏。（二）学前儿童数学教育各年龄阶段目标年龄阶段目标是对总目标架构下的具体化表现的阐述，表述的是对某一特定的年龄阶段进行教育所期望达到的结果。《3—6岁儿童学习与发展指南》中对幼儿数学认知领域提出以下年龄阶段目标。......
2023-07-30
-
学前儿童数学教育设计与指导详细阅读
重叠法就是把两个以上物体重叠在一起进行比较。在实际生活中，随着幼儿年龄的增长，可多鼓励幼儿用目测的方式进行比较，用重叠法和并放法进行验证。（二）量的守恒教育活动的设计与指导量的守恒是指物体的大小、长短等不受物体的外形和摆放位置的变化而改变。量的守恒的教学应在幼儿认识了相应的量的基础上进行。......
2023-07-30
相关推荐