重/难点分析重点分析：从问题想起策略是在学生已经学习了从条件想起策略的基础上进行教学的，两者相辅相成。它对学生理清解决问题的脉络，抓住问题的本质有着重要的作用。突破反思“解决问题的策略——从问题想起”与“解决问题的策略——从条件想起”构成了解决问题的两种基本方法。......
2023-07-27
小数大小比较 | 重难点分析与教学突破策略
【摘要】：重/难点分析重点分析：本课是在学生初步认识了小数的含义和会读写的基础上进行教学的。再让学生选择三种文具的价格，比较这三个小数的大小并交流，通过交流，使学生进一步理解比较小数大小的方法。在教学时，注重唤起学生已有的认知经验，引导学生借助元与角的关系、小数与分数的关系，以及比较整数大小的方法等来自主尝试比较分数的大小。
重/难点
重点：学会比较小数大小的方法。
难点：能用多种方法比较小数的大小。
重/难点分析
重点分析：本课是在学生初步认识了小数的含义和会读写的基础上进行教学的。学会用多种方法比较小数的大小，不仅能发展学生的数感和思维能力，也能沟通整数比较大小与小数比较大小的方法，构建系统的认知结构。
难点分析：一方面，比较小数的大小，需要关注整数部分和小数部分两个层面；另一方面，小数大小的比较与整数大小的比较既有联系又有区别，需要学生理解小数的含义，运用数的意义来比较。因此，运用多种方法比较小数的大小对学生而言有一定难度。
突破策略
一、唤起经验，尝试比较大小
创设生活情境：文具店有各种文具，橡皮0.8元/块，小刀0.9元/把，练习本1.5元/本，铅笔1.3元/支，彩笔8.5元/盒。橡皮和小刀哪个贵一些？引导学生概括问题的本质——比较0.8和0.9的大小。放手让学生运用已有经验来比较这两个数的大小，并交流方法。方法一：化成“角”作单位的数。把0.8元和0.9元分别看成8角和9角，因为8角＜9角，所以0.8元＜0.9元。方法二：化成分数。把0.8化成
，0.9化成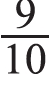
，因为
，所以，0.8元＜0.9元。方法三：画图比较，既可以画直条图来比较，也可以画数轴来比较。方法四：按顺序比较，0.8和0.9的整数部分都是0，再比较小数部分，分别是8和9，8＜9，因此0.8元＜0.9元。在学生交流多种方法之后，引导学生比较这些方法，并让学生选择自己喜欢的方法来说一说。鼓励学生运用“先比较整数部分，再比较小数部分”的简洁方法。
二、迁移方法，深化理解
经历了从方法多样化到方法优化的过程之后，可以让学生选择两种文具来比较它们的价格。如“1.5和1.3的大小”“1.5和0.9的大小”……使学生进一步巩固比较小数大小的方法。之后引导学生小结比较的方法：先从整数部分比起，整数部分大的那个数就大；若整数部分相同，再比较小数部分，小数部分大的那个数就大。再让学生选择三种文具的价格，比较这三个小数的大小并交流，通过交流，使学生进一步理解比较小数大小的方法。
三、多样练习，内化方法
可以设计层次渐进的练习，使学生在练习中经历“直观一抽象”的学习与理解过程。出示练习一：先让学生看图写出小数，再比较大小。通过练习，使学生进一步理解：比1小的小数的大小比较方法——整数部分都是0，就要比较小数部分。比1大的小数的大小比较方法——先比整数部分，整数部分大的那个数就大；整数部分相同，再比小数部分，小数部分大的那个数就大。
1.先写出小数，再比较大小。
通过比较，使学生理解整数部分都是0的小数的大小比较方法，以及整数部分不是0的小数的大小比较方法。
突破反思
比较小数的大小，是对整数大小比较方法的延伸。在教学时，注重唤起学生已有的认知经验，引导学生借助元与角的关系、小数与分数的关系，以及比较整数大小的方法等来自主尝试比较分数的大小。在互动交流中发现普适性的比较方法，得出先比较整数部分，再比较小数部分的简洁方法。通过这样的教学，使学生既开阔了思维，又获得了数学化的简洁方法。
- 详细阅读
-
求简单的经过时间，重难点分析与教学突破策略详细阅读
重/难点分析重点分析：本课是在学生学习了24时计时法的基础上进行教学的。而更复杂的是，计算用普通计时法表示的上午某个时刻到下午某个时刻经过的时间。你知道经过了多长时间吗？突破反思“求简单的经过时间”这节课让生活再次走向了数学，它需要学生在有一定的生活经验后，结合数学方法进行计算。......
2023-07-27
-
小学数学教学突破策略：解决重难点问题详细阅读
在这一过程中，学生除了能正确解决问题外，还可以深切体验从条件想起的策略。根据学生的回答小结：解决这两个问题，我们都用了从条件想起策略，先根据前两个有联系的条件求出“黄花的朵数”这个新条件，这是解决问题的关键一步，这样才能联系另一个条件求出红花的朵数。让学生回顾和比较解决问题的过程，形成对策略的完整认识，积累经验，发展数学思考能力。......
2023-07-27
-
认识年、月、日的重难点与教学突破策略详细阅读
时、分、秒是常见的较小的时间单位，而年、月、日则是较大的时间单位。可以让学生选择一种自己喜欢的方法进行记忆，最后根据大、小月的天数，算一算2016年的天数，由此帮助学生更好地感受年、月、日之间的关系。突破反思年、月、日是生活中常用的时间单位。......
2023-07-27
-
认识24时计时法：重难点分析与教学突破详细阅读
重/难点重点：会用24时计时法表示时间。相比普通计时法，24时计时法在生活中更为科学也更为通用。为了简易、不出错，广播、电视等部门都用24时计时法。教师从而自然而然地揭示了本课新知，并通过这样的认知冲突不仅激发了学生学习的兴趣，而且使学生体验到24时计时法的价值。钟面上时间的行走是直观的，但是不容易从中发现普通计时法和24时计时法之间的联系与区别。......
2023-07-27
-
简单数据汇总 | 重难点分析与突破策略 |详细阅读
重/难点分析重点分析：本课是在学生初步理解了数据和汇总的需要的基础上进行教学的。要想了解某个项目的整体情况，就要对一些有用的数据先整理再汇总。最后汇总出小组同学的生日月份统计表。比如，当要统计的数据比较多时，可以先分组统计，再汇总；把数据按不同的标准分类，可以得到不同的信息；调查的对象不同，得到的结果可能不同。......
2023-07-27
-
认识几分之几 重难点分析与教学策略详细阅读
重/难点分析重点分析：前一节课我们认识了一个物体（或图形）的几分之一，学习了平均分。突破策略一、找准知识生长点，建立几分之几和几分之一的联系认识几分之几的含义，需要充分利用学生对几分之一的已有认知。所以，沟通几分之一与几分之几之间的联系显得尤为重要。学生已有了探究几分之一的经验，对几分之几的探究完全可以独立进行。......
2023-07-27
-
重难点分析和教学突破策略——小学三年级数学详细阅读
重/难点分析重点分析：本节课通过“围一围”“摆一摆”“拼一拼”“量一量”活动，帮助学生进一步理解长方形、正方形的周长以及怎样来计算周长，能为后面学习其他多边形和不规则图形的周长奠定基础。（4厘米）这样12个单个的小正方形的周长和是多少？......
2023-07-27
相关推荐