小数的含义与读写方法及教学策略

2023-07-27 理论教育版权反馈

【摘要】：建立十分之几和一位小数的联系是一个难点，理解小数的意义也是一个难点。小明的身高是1米多，多4分米，4分米用米作单位就是，还可以写成0.4米，1米+0.4米=1.4米。接着，通过多样的练习，使学生进一步了解一位小数的意义和读写方法。

重/难点

重点：认识小数的意义，会读写小数。

难点：理解分数与小数的关系。

重/难点分析

重点分析：本课是在学生认识了十分之几的分数的基础上进行教学的。通过认识小数的意义，建立十分之几和一位小数的联系，并结合生活经验认识更多的小数，拓宽学生对数的意义的认识，为今后学习小数的意义打下基础。

难点分析：小数的意义对于三年级的学生来说是很抽象的。建立十分之几和一位小数的联系是一个难点，理解小数的意义也是一个难点。因此，要充分借助生活经验和分数与小数的联系来引导学生理解小数的意义，以此帮助学生化解难点，顺利构建概念。

突破策略

一、与经验相连，理解小数的意义

先带领学生复习长度单位和货币单位之间的关系，出示如下两个例子（见下页图），让学生想一想1厘米与1分米的关系、1角与1元的关系，从而明确十进制关系。这样便充分调动了学生的生活经验和学习经验，帮助学生实现了由分数向小数领域的跨越。

接着，以■分米为例，引导学生分析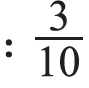 pagenumber_ebook=138,pagenumber_book=125 分米不满1分米，还可以写成0.3分米，0.3读作零点三。让学生思考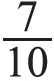：分米可以怎样改写？学生仿照上面的例子来写一写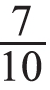：分米不满1分米，可以写成0.7分米，0.7读作零点七。再引导学生在直条图上表示出0.3和0.7，使学生进一步理解0.3分米和0.7分米只占1分米的直条的一部分，明确零点几比1小。同样，可以让学生用直条表示1元，再在直条上表示出0.4元和0.8元，进一步体会零点几比1小。

二、与生活相连，内化小数的意义

出示“小明的身高是1米4分米”，思考：小明的身高是几米多？多多少？用米表示是多少米？出示“笔记本的单价是3元5角”，思考：笔记本的单价是几元多，多多少？用元表示是多少元？引发学生借助已有的学习经验来分析推理。小明的身高是1米多，多4分米，4分米用米作单位就是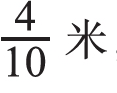 pagenumber_ebook=138,pagenumber_book=125 ，还可以写成0.4米，1米+0.4米=1.4米。所以1米4分米还可以写成1.4米，1.4读作一点四。笔记本的单价是3元多，多5角，5角用元作单位就是 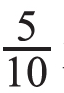pagenumber_ebook=139,pagenumber_book=126 元，还可以写成0.5元，3元+0.5元=3.5元。所以3元5角还可以写成3.5元，3.5读作三点五。

接着，组织学生说说我们已经学过哪些数。学生能够想到整数和分数。表示物体个数的1，2，3……是自然数，0也是自然数，它们都是整数。还学过分数，如……而刚才学习的0.4，0.8，0.3，0.7，1.4，3.5，与之前学过的数不同，可以称为小数。再引导学生研究小数各部分的名称：小数中的圆点叫作小数点，小数点左边的部分是整数部分，右边的部分是小数部分，直观呈现各部分名称。再让学生来说一说某一个小数的整数部分是多少，小数部分是多少，进一步内化对小数意义的理解。

三、多样拓展，进一步内化小数的意义

首先，出示直条图（见下图），让学生来填一填。在填写整数、分数和小数的过程中，进一步沟通分数与小数的关系，进一步理解几厘米等于分米，也等于零点几分米，沟通长度单位间的十进制关系。

接着，出示生活中的实物及其单价，让学生用小数表示它们的单价。如蛋糕2元3角、一袋面包4元5角、一盒牛奶5元8角、一盒巧克力18元5角，使学生理解几元几角可以写成几点几元，进一步深化对一位小数的意义的理解。

再出示看图填数的活动，让学生先看图，分析涂色部分可以用表示，再将其改写成小数，进一步理解十分之几和零点几之间的关系。最后出示数轴图，让学生先填小数，再比较分析，发现0～1之间的数是零点几，比0大而比1小；1～2之间的数是一点几，比1大而比2小；2～3之间的数是二点几，比2大而比3小；3～4之间的数是三点几，比3大而比4小……进一步深化对一位小数的理解。

突破反思

学生从认识整数、分数到认识小数，是认数历程的一次飞跃。在教学时，注重结合学生的生活实际和认知经验，让他们从单位之间的进率入手，理解十分之几可以写成零点几，建立一位小数的模型，学会读写一位小数的方法。接着，通过多样的练习，使学生进一步了解一位小数的意义和读写方法。这样教学，不仅激发了学生的已有认知和学习的积极性，也有效突破了难点，有利于培养学生的数感。

小数的含义与读写方法及教学策略

相关推荐