一个数字的几分之几最高可以是多少

2023-07-27 理论教育版权反馈

【摘要】：重/难点分析重点分析：本课是在学生初步认识了一个整体的几分之几、会用除法求一个数的几分之一的基础上进行教学的。突破策略一、动手和动脑结合，构建解决问题的模型创设情境：妈妈买了6个苹果，把这些苹果的分给小红，小红一共分得多少个苹果？因此，在教学时，要引导学生紧扣分数的意义来理解，求一个数的几分之几是多少就是把总数平均分成几份，再求其中的几份。

重/难点

重点：会用先除再乘的方法求一个数的几分之几是多少。

难点：理解分数中的分母与除法中的除数、分数中的分子与乘法中的乘数的对应关系。

重/难点分析

重点分析：本课是在学生初步认识了一个整体的几分之几、会用除法求一个数的几分之一的基础上进行教学的。通过分一分、画一画等活动，知道把一个整体平均分成几份，求其中的几份是多少，就是把总数先平均分成几份，求出其中一份是多少，再用乘法求出几份是多少。这样的教学过程，有助于学生建立起分数与平均分、乘法之间的内在联系，也为今后学习分数实际问题奠定基础。

难点分析：求一个数的几分之几是多少对三年级的学生来说是有一定难度的。一方面，总数的几分之几较抽象，在此基础上学习一个整体的几分之几是多少有一定难度；另一方面，在求一个数的几分之几是多少时，要先用除法求出一份是多少，再用乘法求出几份是多少。因此，正确理解分数的意义，构建分数与除法和乘法之间的联系是学生学习的难点。

突破策略

一、动手和动脑结合，构建解决问题的模型

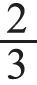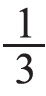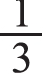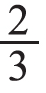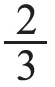创设情境：妈妈买了6个苹果，把这些苹果的 pagenumber_ebook=133,pagenumber_book=120 分给小红，小红一共分得多少个苹果？可以让学生先动手分一分，再说说的含义：把6个苹果平均分成3份，每份是这些苹果的，2份就是2个，就是。学生通过动手分一分可以清楚地看出小红分得4个苹果。此时，引导学生抽象出实际问题的本质——求6个苹果的 pagenumber_ebook=133,pagenumber_book=120 是多少。让学生动脑想一想，怎样用算式计算小红分得的苹果个数。根据直观图示，学生能够想到先把6个苹果平均分成3份，求出每份是2个，算式为6÷3=2（个），再求出2份是多少个，用乘法来解答：2×2=4（个）。让学生说一说两个算式的意义，可以引导学生将算式与情境图对应起来理解。也可以列出综合算式：6÷3×2，让学生说一说6÷3表示什么，为什么要乘2，从而把分数与除法、乘法建立联系，使学生体会到要求6个苹果的 pagenumber_ebook=133,pagenumber_book=120 是多少，可以先用总数6除以份数3得到每份的个数，再用每份的个数乘其中的2份，就能求得总数的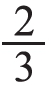是多少。其中，除数是平均分的份数，乘数表示其中的几份，帮助学生构建解决问题的模型。

二、多角度对比，深化认识

在学生初步理解了“求6个苹果的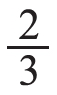 pagenumber_ebook=133,pagenumber_book=120 是多少”可以用先除后乘的方法计算后，及时出示另一个问题：如果把这6个苹果的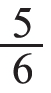送给小红，小红一共能得多少个苹果？让学生用自己喜欢的方法来解答，并组织学生交流。学生可以用画图的方法来解答，把6个苹果平均分成6份，再把其中的5份涂上颜色，可以看出小红能得5个苹果。还可以想这是“求6个苹果的 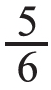pagenumber_ebook=133,pagenumber_book=120 是多少”，可以用先除再乘的方法来解答：6÷6x5。再让学生说说算式的意思，使学生明白：先把总数6个苹果平均分成6份，用除法解决，其中的5份就是乘5，用乘法解决。

接着，让学生比较刚才研究的两个问题：求6个苹果的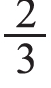 pagenumber_ebook=134,pagenumber_book=121 是多少？求6个苹果的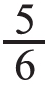是多少？提出问题：同样是把6个苹果中的一部分分给小红，为什么两次给的个数不同？通过比较，学生能够得出：总数相同，平均分的份数不同，表示其中的几份也不同，所以求得的个数也不同。再引导学生思考：怎样求一个数的几分之几是多少？学生通过比较能够得出：“总数÷平均分的份数×取的份数=一共得到的个数”，帮助学生构建解决这类问题的模型。三、操作与思考结合，内化理解

出示对比题：（1）12个圆片，拿出它的 pagenumber_ebook=134,pagenumber_book=121 。要拿出多少个？（2）16个圆片，拿出它的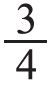。要拿出多少个？先让学生摆一摆，再说一说是怎样想的。通过交流，学生能够得出：问题（1）是把12个圆片平均分成4份，每份就是3个，拿出其中的3份，就是有3个3，因此可以用先除再乘的方法来解答：12÷4×3。问题（2）是把16个圆片平均分成4份，每份就是4个，拿出其中的3份，就是3个4，也可以用先除再乘的方法来解答：16÷4×3。在此基础上组织学生讨论：为什么同样是拿出 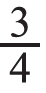pagenumber_ebook=134,pagenumber_book=121 ，拿出的个数却不一样？比较后得出：因为平均分的总数不同，它的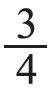也就不同。但是，它们都是求一个数的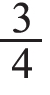，因此都可以用“总数÷平均分的份数×拿出的份数=拿出的个数”来计算。

接着，再出示练习。

先分一分，再填空。

让学生先独立试一试，再组织交流：把（　）平均分成（　）份，每份是（　）个，拿出其中的（　）份是（　）个。引导学生列出算式，使学生把图意与算式正确地对接起来。最后再组织学生比较，在解决“求总数的几分之几是多少”的问题时，有什么相同之处。最后引导学生小结：求一个数的几分之几是多少，可以先分一分，再通过观察得出结果；也可以用先除再乘的方法来计算，先用除法求出每份是多少，再用乘法求出其中的几份是多少。

最后，出示一个隐藏条件的实际问题：有一块巧克力（见下图），小春吃了这块巧克力的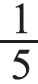 pagenumber_ebook=135,pagenumber_book=122 ，小冬吃了这块巧克力的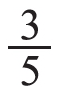。他们各吃了几小块？

在解决这个问题时，鼓励学生选择适合自己的方法，如在图中分一分，看一看；用先除再乘的方法来计算，并把两种方法求得的结果进行对比，验证思路的正确性。

经过多次的比较活动，使学生逐渐理解“求一个数的几分之几是多少”，可以用先除再乘的方法来解答，关键要明确总数、平均分的份数以及取的份数这几个要素，使学生进一步理解分数的意义以及解决实际问题的方法。

突破反思

学习求一个数的几分之几是多少是建立在学习过平均分知识的基础之上的。因此，在教学时，要引导学生紧扣分数的意义来理解，求一个数的几分之几是多少就是把总数平均分成几份，再求其中的几份。建立起平均分的份数与分母、每份的个数与表示的份数之间的对应关系，从而使学生学会把“求一个数的几分之几是多少”转化成“先把总数平均分成几份，求出一份是多少，再求几份是多少”的实际问题。这样的教学，不仅有利于学生理解知识的本质，更有利于学生构建解决类似问题的模型。

一个数字的几分之几最高可以是多少

相关推荐