重/难点分析重点分析：本课是在学生初步认识了一个整体的几分之几、会用除法求一个数的几分之一的基础上进行教学的。突破策略一、动手和动脑结合，构建解决问题的模型创设情境：妈妈买了6个苹果，把这些苹果的分给小红，小红一共分得多少个苹果？因此，在教学时，要引导学生紧扣分数的意义来理解，求一个数的几分之几是多少就是把总数平均分成几份，再求其中的几份。......
2023-07-27
数的几分之一是多少？解析与计算方法
【摘要】：重/难点分析重点分析：本课是在学生初步认识了一个整体的几分之一的基础上进行教学的。经过多次的比较活动，使学生逐步理解求一个数的几分之一可以用除法来解答，关键要明确总数、平均分的份数，使学生进一步理解分数的意义，以及解决实际问题的方法。
重/难点
重点：会用除法求一个数的几分之一是多少。
难点：理解分数中的分母与除法中的除数的对应关系。
重/难点分析
重点分析：本课是在学生初步认识了一个整体的几分之一的基础上进行教学的。让学生通过分一分、画一画等活动，知道把一个整体平均分成几份就是把总数平均分成几份，从而确定用除法计算。这样的思考过程，有助于学生建立对应思想，理解数学知识之间的内在联系，为今后的学习提供了开放的思考空间，奠定了坚实的基础。
难点分析：关于求一个数的几分之一是多少对学生来说是比较抽象的。一方面，学生对分数意义的理解还不够深刻，在此基础上学习一个整体的几分之一是多少有一定难度；另一方面，理解分数与除法的关系对学生来说也有一定难度。因此，深刻理解分数的意义，明确分数与除法之间的关系是学生学习的难点。
突破策略
一、借助操作，理解分数的意义
创设情境：王老师买了6个皮球，把其中的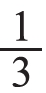
奖励给三（1）班，三（1）班分得多少个皮球？你能用自己的方式表示王老师分的过程和结果吗？引导学生尝试将小圆片当皮球来分一分。如果把6个皮球平均分给3个班，每个班得到了几个皮球？组织学生交流想法：把6个皮球看作一个整体，平均分成3份，每份就是
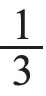，因此三（1）班分得这些球的
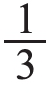。从图中就可以看出每份是2个，因此三（1）班分得2个皮球。接着，让学生观察图示和结果，说说怎样用算式来表达三（1）班分得多少个皮球。学生能够想到用“总数÷份数=每份的个数”，即6÷3=2（个）。再让学生说一说算式中6，3，2分别表示什么意思。从而将分数与除法建立联系，使学生体会到求6个皮球的
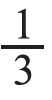是多少，可以用总数除以份数得到每份的个数。其中，分母相当于平均分的份数，分子相当于要分的总数，帮助学生构建解决问题的模型。
二、变式比较，凸显本质
在学生初步理解了求6的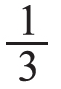
是多少可以用除法计算后，及时出示另一个问题：如果把这6个皮球平均分给二年级的2个班，每个班分得几分之几？是几个？创设开放的情境，让学生用自己喜欢的方法来解答，并组织学生交流。问题一，要突出“把6个皮球看作一个整体，平均分成2份，每份就是这些皮球的
”。问题二，要激发学生用联系的观点来解释思考：把6个皮球平均分成2份，求每份是多少个，用“总数÷份数=每份的个数”，即6÷2=3（个）。在解决问题的基础上，组织学生进行比较：同样是把6个皮球平均分，为什么每份的个数不同？引导学生关注平均分的份数，并得出结论：总数相同，平均分的份数不同，每份的个数也不同。引导学生再思考：怎样求一个数的几分之一是多少？学生通过比较能够得出“总数÷份数=每份的个数”。
三、比较学习，内化理解
出示对比题：（1）8个圆片，拿出它的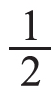
。拿出多少个？（2）10个圆片，拿出它的
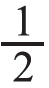。拿出多少个？先让学生摆一摆，再说一说是怎样想的。通过交流，学生能够得出：问题（1）是把8个圆片平均分成2份，每份就是4个，用除法，8÷2=4（个）；问题（2）是把10个圆片平均分成2份，每份是5个，用除法，10÷2=5（个）。在此基础上组织学生讨论：为什么同样拿出
，拿出的个数却不一样？比较后得出：因为平均分的总数不同，它的
也就不同。但是它们都是求一个数的
，因此都可以用“总数÷份数=每份的个数”来计算。
出示实际问题：每页可以写16个大字，小明写了一页的
，小红写了一页的
。他们各写了多少个字？让学生先独立解决再交流：小明写的个数是16÷2=8（个），小红写的个数是16÷4=4（个）。再组织学生比较：这次总数相同了，为什么两人写的个数还是不一样？由此小结：一个是求16个大字的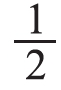
，另一个是求16个大字的
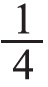。总数相同，平均分的份数不同，因此每份的个数就不同。
经过多次的比较活动，使学生逐步理解求一个数的几分之一可以用除法来解答，关键要明确总数、平均分的份数，使学生进一步理解分数的意义，以及解决实际问题的方法。
突破反思
本课教学建立在学生学习了平均分知识的基础之上。因此，在教学时，紧扣分数的意义引导学生理解求一个数的几分之一就是把总数平均分成几份，使学生建立起平均分的份数与分数的分母之间的对应关系，从而使学生学会把“求一个数的几分之一”转化成“总数平均分成几份，求一份是多少”的实际问题。这样的教学，不仅有利于学生理解知识的本质，更有利于学生构建解决问题的模型。
- 详细阅读
-
认识分数：图形平均分成几份，每份是几分之一详细阅读
结合图形，让学生理解：把一个图形平均分成了几份，每份就是它的几分之一。突破反思“认识几分之一”是让学生在掌握了一些整数知识的基础上初步认识分数的含义，从整数到分数是数的概念的一次扩展。......
2023-07-27
-
四宫数独解析成功！标准数独技巧，快速解题的关详细阅读
图3-1所示的是一道四宫数独原题，我们用排除法解答该题。利用A4格的数字4对一宫进行排除，得到一宫内B2格填入数字4。经过判断发现三宫这时缺数字1和2。填完一宫和三宫后，二宫和四宫也可以用相同的思路来填数。数独解题过程中往往出现在同一个情况下可以使用不同的方法和思路，而如何寻找线索并且将思路连贯起来，就是快速解题的关键所在了。......
2023-10-29
-
标准数独六宫解析技巧，附实例详细阅读
图3-4所示的是一道六宫数独原题，我们来用本书所学的宫内排除法和行列排除法技巧解答该题。从前面所学的内容，我们了解到，某个区域内数字偏少，并不一定就无法用别的数字对其找出线索。利用F1格的数字2对六宫进行排除，得到E4格可以填入数字2。上述两步就是针对列使用的行列排除法。总体来看，以宫作为主要观察线索会使解题整体节奏更简捷有效，但在宫没有明显线索时，观察行列效果会更好。......
2023-10-29
-
初级九宫数独解析及标准数独技巧篇详细阅读
再利用三宫和九宫的数字1对六宫进行排除，得到D8格填入数字1。五宫剩余三个空格缺少数字4、6和9，利用四宫和六宫的数字9，六宫的数字4对五宫进行排除，可以得到E5格填入数字9，D5格填入数字4和F5格填入数字6。图3-11通过本题的讲解，相信大家对于九宫数独的宫内排除法、区块排除法和行列排除法如何应用有了大体了解。初学排除法时应多按宫的线索加以观察，尽量使用宫内排除法。......
2023-10-29
-
小学数学三年级的整体几分之一的认识和突破策略详细阅读
重/难点分析重点分析：本课是在学生初步认识了一个物体的几分之一的基础上进行教学的。再出示另一个盒子，盒子里有6个桃子，平均分成2份，每份是这盒桃子的几分之几？......
2023-07-27
-
确定冷却数和特性数的方法与注意事项详细阅读
图7-11T2—K曲线由于冷却塔内气水处于热平衡状态，即有下式成立式中符号同前，则有假设在整个塔内该式成立，则有式中T1、T2分别为进水温度和出水温度。图7-12气水比及冷却数的确定表7-1值选择范围......
2023-06-19
-
应用判别式解析21.4根数详细阅读
对于一元二次方程ax2＋bx＋c＝0（a≠0）．当b2－4ac＞0时，方程_______________________；当b2－4ac＝0时，方程________________________；当b2－4ac＜0时，方程_______________________．1．方程4x2－3x＋1＝0的根的情况是（ ）．A．有两个都是负的实数根B．有两个都是正的实数根C．有两个相等的实数根D．没有实......
2023-07-03
相关推荐