认识分数：图形平均分成几份，每份是几分之一

2023-07-27 理论教育版权反馈

【摘要】：结合图形，让学生理解：把一个图形平均分成了几份，每份就是它的几分之一。突破反思“认识几分之一”是让学生在掌握了一些整数知识的基础上初步认识分数的含义，从整数到分数是数的概念的一次扩展。

重/难点

重点：认识几分之一及其大小。

难点：理解几分之一的含义。

重/难点分析

重点分析：本节课的重点是初步理解分数的含义。结合具体情境初步理解把一个物体（或图形）平均分成若干份，其中的一份或几份可以用分数表示，既是比较分数大小，探索同分母分数加减法的前提，也是今后进一步认识分数，抽象概括分数意义的重要基础。

难点分析：本节课的难点是根据给出的图形，估计各部分大约占整体的几分之几。在这样的问题情境中，学生不仅需要合理把握给出的各部分的大小以及它们与整体之间的关系，而且需要把这种关系与头脑中储存的相关的分数进行适当的对比，进而做出判断和选择。显然，这个过程是有一定难度的。

突破策略

一、创设情境，导入新课

结合具体情境，通过谈话自然地引出问题：从图上看，他们带了哪些食品？把每种食品平均分成2份，每人分得多少？学生独立思考后指名汇报，全班交流。

通过平均分苹果、矿泉水，发现每种食品每份的个数都是整数，接着自然过渡到将一个蛋糕平均分成2份，这时，学生会想到每人分得半个蛋糕，感受到不能再用整数表示了，由此引发学生的好奇心：该用什么样的数表示半个蛋糕呢？这样便可以引入本节课的内容，同时也让学生体会到数学知识的产生和形成源于实际生活的需要，数学知识与生活实际是紧密联系的。

二、认识分数，理解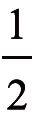 pagenumber_ebook=73,pagenumber_book=60 的含义

1.直观操作，初步感知。

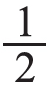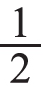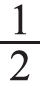把一个蛋糕平均分成2份，每人分得半个，可以用怎样的数表示呢？由此引出分数的知识。由于是初次接触分数，教师要讲解清楚：把一个蛋糕平均分成2份，每人分得半个，左边半个是2份中的1份，右边半个也是2份中的1份，因此，它们都是这个蛋糕的 pagenumber_ebook=73,pagenumber_book=60 。

2.读写结合，认识 pagenumber_ebook=73,pagenumber_book=60 的含义。

读写 pagenumber_ebook=73,pagenumber_book=60 时，教给学生分数各部分的名称以及表示的意义，另外还要强调分数的读写方法。可以让学生伸出手指跟着教师比画，先写的短横线表示把这个蛋糕平均分，它叫分数线；在分数线的下面写2，表示平均分成2份，2叫分母；在分数线的上面写1，表示其中的1份，1叫分子，让学生跟着教师再写两遍，读两遍，以便加强记忆。

3.操作理解，深入认识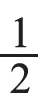 pagenumber_ebook=74,pagenumber_book=61 。

为了进一步理解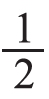 pagenumber_ebook=74,pagenumber_book=61 ，让学生拿出一张长方形纸，先折一折，再把它的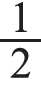涂上颜色，之后展示学生的不同折法。

提问：为什么折法不同却都可以表示这张纸的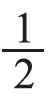 pagenumber_ebook=74,pagenumber_book=61 ？接着由教师进行小结：无论怎样折，只要把这张纸平均分成2份，每份都是它的。

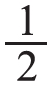4.辨别判断，巩固认识。

让学生判断下面哪些图形的涂色部分可以用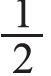 pagenumber_ebook=74,pagenumber_book=61 表示，哪些不可以。

通过交流可以让学生理解：要想得到一个图形的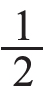 pagenumber_ebook=74,pagenumber_book=61 ，必须把它平均分成2份，其中的1份就是它的。

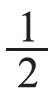三、认识几分之一，比较几分之一的大小

1.动手操作，认识几分之一。

为了巩固学生对几分之一的认识，安排操作活动，让学生通过折圆片并涂色的方法，得到自己想要的几分之一，并在黑板上展示学生的作品。

结合图形，让学生理解：把一个图形平均分成了几份，每份就是它的几分之一。

2.比较分数的大小。

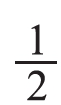结合具体的图形，比较的大小，从涂色部分的大小，可以看出 pagenumber_ebook=75,pagenumber_book=62 大于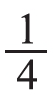，用同样的方法还能比较出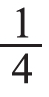大于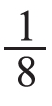。这时，教师适时点拨提问如果把这张圆形纸片继续对折下去，还能得到几分之一呢？它们之间用什么符号连接呢？让学生的思维得到进一步发散和提升。

继续比下去，会发现分母越大，分数越小，让学生切实感受到：把同一个图形，平均分成的份数越多，每份就越小。

突破反思

“认识几分之一”是让学生在掌握了一些整数知识的基础上初步认识分数的含义，从整数到分数是数的概念的一次扩展。无论在意义上、读写方法上，还是在计算方法上，分数和整数都有很大的差异。

上课伊始，创设一个简单的分物体的情境，活跃了课堂气氛，很好地调动了学生学习的积极性，使他们很快地进入新课的学习中。在知识层面上，从整数的平均分开始，从把4个苹果平均分成2份，到把2瓶水平均分成2份，再到把1个蛋糕平均分成2份，引出了分数。这便渗透了“平均分”的概念，并使学生发现了问题：半个蛋糕怎样用数表示？这一问题用以前的知识无法解决，从而导入新课、揭示课题。另外，在本课教学中设计了形式多样的活动，让学生通过经历折长方形和圆形纸片的过程，体会到分数的意义；通过交流，使学生整体把握了分数的意义。此外，在这节课上，应该注重培养学生完整表达的能力。

认识分数：图形平均分成几份，每份是几分之一

相关推荐