贝叶斯决策理论是统计方法处理模式分类问题的基本理论之一。那么,利用贝叶斯公式可以得到后验概率基于最小错误率的贝叶斯决策规则为:如果,也就是说,如果p,那么将模式x赋予类ωi,即x∈ωi。上述理论中,每个类的出现概率以模式的条件概率密度函数必须是已知的。由于这些原因,贝叶斯决策理论在实际应用中通常要假设各种概率密度函数的解析式,以及从每类样本模式估计的必要参数。......
2023-06-28
无风险证券的收益和价格都标准化为1,风险证券的收益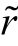 =
=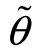 +
+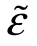 ,其中
,其中 服从正态分布N(0,σ2)。
服从正态分布N(0,σ2)。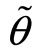 是取两个值θ1或θ2(θ1<θ2)的随机变量,
是取两个值θ1或θ2(θ1<θ2)的随机变量,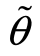 取θ1和θ2的概率分别为π1、π2(π1+π2=1)。
取θ1和θ2的概率分别为π1、π2(π1+π2=1)。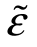 和
和 相互独立,
相互独立, 的均值为0。交易在期初进行,
的均值为0。交易在期初进行,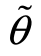 、
、 的值在期末为交易者所共知。
的值在期末为交易者所共知。
机构投资者拥有中性的风险偏好,其“市场势力”不仅影响市场价格,而且能够影响散户的信念。机构投资者期初持有一个单位的货币,没有风险证券,是证券交易的买方。股票市场的信息非对称表现为机构投资者在期初已经知道 的实现值θ,而散户不知道。设散户构成测度为1的连续统集合(continuum),他们期初持有总量为w0单位的货币,1个单位的风险证券。散户具有非递增的绝对风险厌恶,其效用函数u(.)是单调递增的严格凹函数。若散户们的决策组合为b单位的货币、α单位的风险资产,则散户的最优策略为如下最优化问题的解:
的实现值θ,而散户不知道。设散户构成测度为1的连续统集合(continuum),他们期初持有总量为w0单位的货币,1个单位的风险证券。散户具有非递增的绝对风险厌恶,其效用函数u(.)是单调递增的严格凹函数。若散户们的决策组合为b单位的货币、α单位的风险资产,则散户的最优策略为如下最优化问题的解:
其中,g(θ|v)为散户观察到证券均衡价格后关于 取值θ的后验概率信念。
取值θ的后验概率信念。
分别为散户在状态θ1,θ2时的期末财富。
在上述模型,买卖双方可以递交各自的需求函数,以供求相等时得到的市场均衡价格来完成交易。由于α+β=1,故一个可取的方法就是机构投资者根据他掌握的信息首先提出证券交易价格v(θ),散户随后决定持有数量α,1-α就是机构投资者的购买量。因此,机构投资者i的策略是v(θ):{θ1,θ2}→R,即机构投资者决定价格v(θ)。散户的策略是α(v):R→[0,1]。α(v)由散户求期望效用最大化决定。
博弈所用的均衡是完美贝叶斯均衡,它是指一对策略(v(.),α(.))和一组后验信念g(.|.),满足:
(C1)散户为贝叶斯理性,即对任给的可行v,g(.|v)是观测到证券均衡价格v后,基于先验信念(π1,π2),按贝叶斯推断形成的对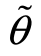 取值θ的后验信念。
取值θ的后验信念。
(C2)任给v,α(v)是散户的最优选择,即
(C3)任给θ,v(θ)是机构投资者的最优定价,即
有关中国基金业:管制、投资与激励的文章

贝叶斯决策理论是统计方法处理模式分类问题的基本理论之一。那么,利用贝叶斯公式可以得到后验概率基于最小错误率的贝叶斯决策规则为:如果,也就是说,如果p,那么将模式x赋予类ωi,即x∈ωi。上述理论中,每个类的出现概率以模式的条件概率密度函数必须是已知的。由于这些原因,贝叶斯决策理论在实际应用中通常要假设各种概率密度函数的解析式,以及从每类样本模式估计的必要参数。......
2023-06-28

在公司投资活动中,投资收益确定的投资称作无风险投资,进行投资决策分析时以收益率为标准。由于实际投资活动中存在多期的投资收益率,决策时多使用平均收益率。表4-2并购公司的期望收益率计算表4.1.4公司并购组合收益率组合收益率是指公司并购完成后新公司的收益率,可用并购各方的期望收益率和并购各方所占股份的比例来计算。换股比率是指在公司并购过程中确定的,目标公司的新定每股股票的并购价格与并购公司的股票价格的比率。......
2024-09-20

SBRCM的建立,是为更好地在V&V活动的实践中,对V&V活动的风险和费用进行描述,从而进一步促进V&V活动的剪裁优化和后续阶段的可信性评估工作。6)对于Ai,其APL为xi,执行该项活动后,当前风险损失为可能产生的风险损失和以执行水平xi执行后所约减的风险损失之差:。8)基于S0,且所有风险源导致的所有风险事件均发生,则极限风险损失值为:9)基于策略S,记可测的、确定的函数为相应策略下的费用。图4.3表示了一个SBRCM的概貌。......
2023-08-15

,xn}输出:未知样本X所属类别号3.朴素贝叶斯分类算法演示表3-9朴素贝叶斯示例数据集样本X7={打喷嚏,建筑工人,?朴素贝叶斯分类算法的优点在于容易实现,在大多数情况下所获得的结果比较好。......
2023-11-08

母公司必须保持与子公司的风险资本要求同等的资本金水平,以防范子公司财务状况恶化引发的风险。如果风险模拟测试中风险溢价部分超出了预期违约损失,超出部分将会累计到准备金负债中。......
2023-11-29

每次率定结束后,由以下4个统计特征指标评定水文模型的运行。根据以上所述标准评价每次率定过程。其中,分裂样本检验是最为普遍使用的方法,它将可利用的测定时间序列一分为二,一部分序列用于模型参数率定,另一部分的资料用于模型验证,通过比较输出变量和测量值,检验模型的正确性。......
2023-06-24

朴素贝叶斯分类器进行目标分类的基本思想是利用特征项和类别的联合概率来估计给定目标的类别概率。理论上,朴素贝叶斯分类器与其他分类方法相比具有最小的误差率。但是该模型在分类识别中假设特征项之间相互独立,而这个假设在实际应用中往往是不成立的,这给朴素贝叶斯分类器的正确分类带来了一定影响。因此,近年来大量的研究工作致力于改进朴素贝叶斯分类器,主要集中在选择特征子集和放松独立性假设在两个方面。......
2023-06-28

策略和组织管理中的风险是指云服务供应商在部署云服务过程中的不完备所带来的风险。减少或者避免策略和组织管理中的风险问题可以更好地保证提供安全的云计算服务。云计算面临着以下的策略和组织管理方面的风险:1.锁定风险用户不能方便地迁移数据/服务到其他云服务提供商,或迁回本地。......
2023-11-18
相关推荐