多准则决策分析主要包括数据准备及预处理、缓冲区分析、缓冲区域分级权重赋值、按权重叠置分析、输出结果专题地图等步骤。图3.26纽约市消防站负荷状况从数学的角度，缓冲区定义为给定一个空间对象或集合，确定其邻域，邻域半径即缓冲距离(宽度)，是缓冲区分析的主要数量指标，可以是常数或变量。按照表3.12的划分依据，通过叠置分析将服务区划分为低值区、中值区、高值区三个等级，从而得到纽约市医院空间布局优化图。......
2023-06-15
期望值准则法的优化的分析介绍
【摘要】：期望值准则法是利用决策益损表，计算各种方案在各种自然状态下的期望益损值，按照最大期望收益值标准和最小期望损失值标准，对期望益损值进行比较、分析，最后选出最优方案。2）计算期望损失值，并选择最小期望损失值对应的方案为最优方案。表10-7 益损值表 故应选择期望损失值最小的组建大型车队的方案。
期望值准则法是利用决策益损表，计算各种方案在各种自然状态下的期望益损值，按照最大期望收益值标准和最小期望损失值标准，对期望益损值进行比较、分析，最后选出最优方案。
1.最大期望收益值标准
决策步骤如下：
1）编制不同方案在不同自然状态下的收益值表。
2）计算不同方案的期望收益值
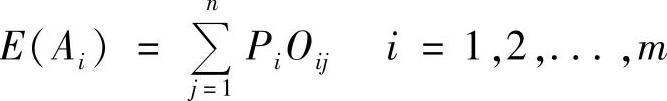
式中，Pi是第i种自然状态出现的概率，i=1，2，…，m；
Oij是第i个方案在第j种自然状态下的收益值，i=1，2，…，m；j=1，2，…，n。
3）选择期望收益值最大的方案为最优方案
E（Ai）=max{E（Ai）}，i=1，2，…，m
[案例1] 某物流公司准备组建车队，并有三个方案：组建大型车队、组建中型车队和组建小型车队。据估计，该物流公司业务量大的可能性是50%，业务量中的可能性是30%，业务量少的可能性是20%。此时，问题就变成了风险型的决策问题了。我们用最大期望收益值标准迸行决策，见表10-6。
表10-6 益损值表（单位：万元）
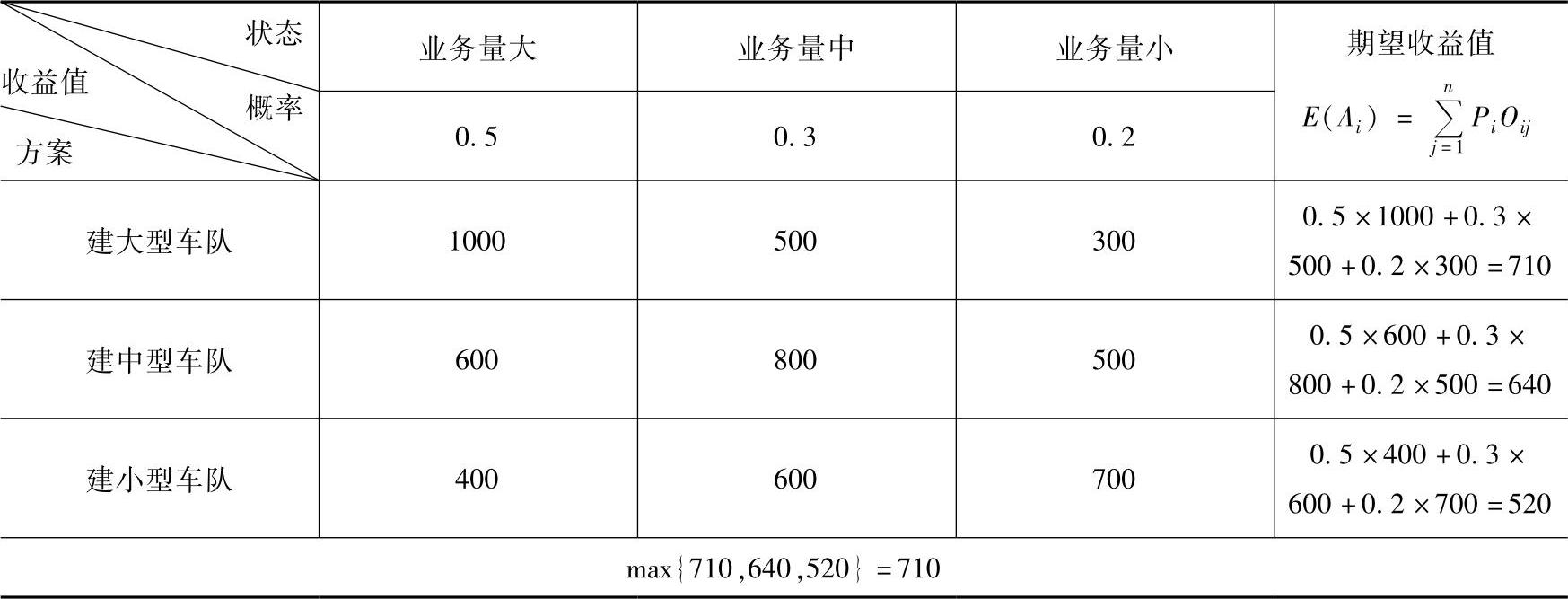
故应选择期望收益值最大的组建大型车队的方案。
2.最小期望损失值标准
最小期望损失值标准的基本思想是：计算各种情况下，各行动方案的损失值，然后，计算每种方案的期望损失值，选择最小期望损失值对应的方案为最优方案。
计算步骤如下：
1）编制不同方案在不同自然状态下的损失值表。损失值的计算方法是：用每种状态下的最大收益值减去该状态下各个方案的收益值，就得到了损失值表。
2）计算不同方案的期望损失值
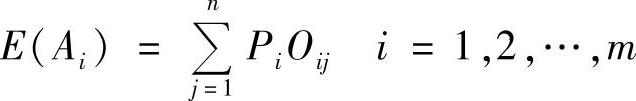
式中，Pi是第i种自然状态出现的概率，i=1，2，…，m；
Oij是第i个方案在第j种自然状态下的损失值，i=1，2，…，m，j=1，2，…，n
3）选择期望损失值最小的方案为最优方案
E（Ai）=min{E（Ai）}，i=1，2，…，m
[案例2] 仍以[案例1]为例，用最小期望损失值标准迸行决策。
解：
1）编制期望损失值表见表10-7。
2）计算期望损失值，并选择最小期望损失值对应的方案为最优方案。计算结果见表10-7。
表10-7 益损值表 （单位：万元）
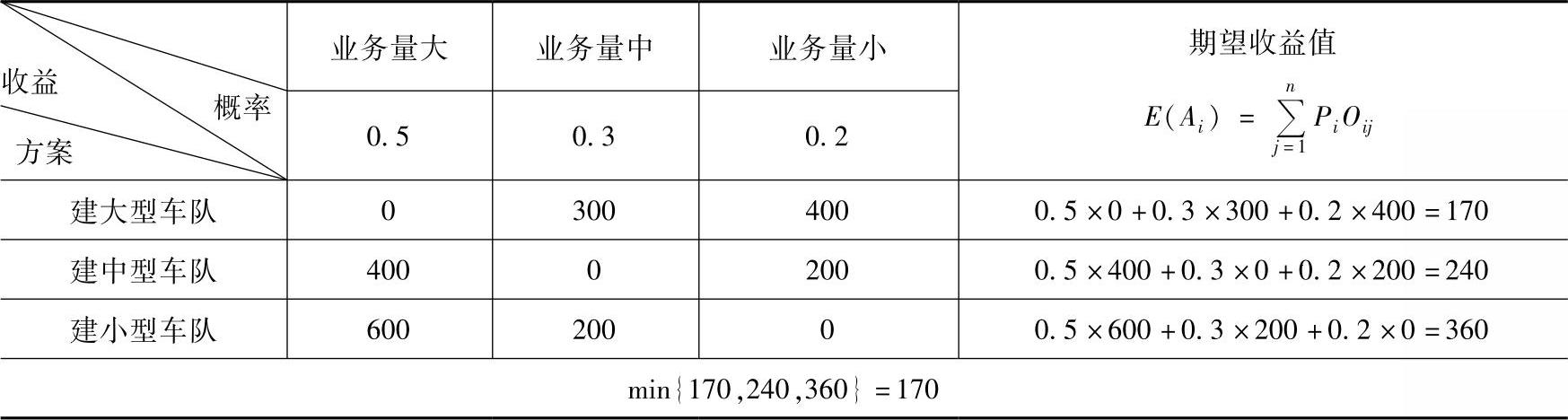
故应选择期望损失值最小的组建大型车队的方案。
3.最大可能收益值标准
风险型决策问题中，每种状态的发生都有一个概率值，某种状态的概率值越大，说明该种状态发生的可能性越大。基于这种想法，在风险型决策问题中，若某种状态的概率远比其他状态的概率大得多的时候，就可以忽略其他状态，而只考虑概率特别大的这一种状态。即把风险型决策问题转换成确定情况下的决策问题进行决策，这就叫最大可能收益值标准。
[案例3] 仍以[案例2]为例，三种状态出现的概率调整为：0.7、0.2、0.1，此时，业务量大的情况出现的可能性非常大，故不再考虑其他两种情况，只考虑业务量大这一种情况。分别用最大收益标准和最小损失标准决策。见表10-8。
表10-8 益损值表 （单位：万元）
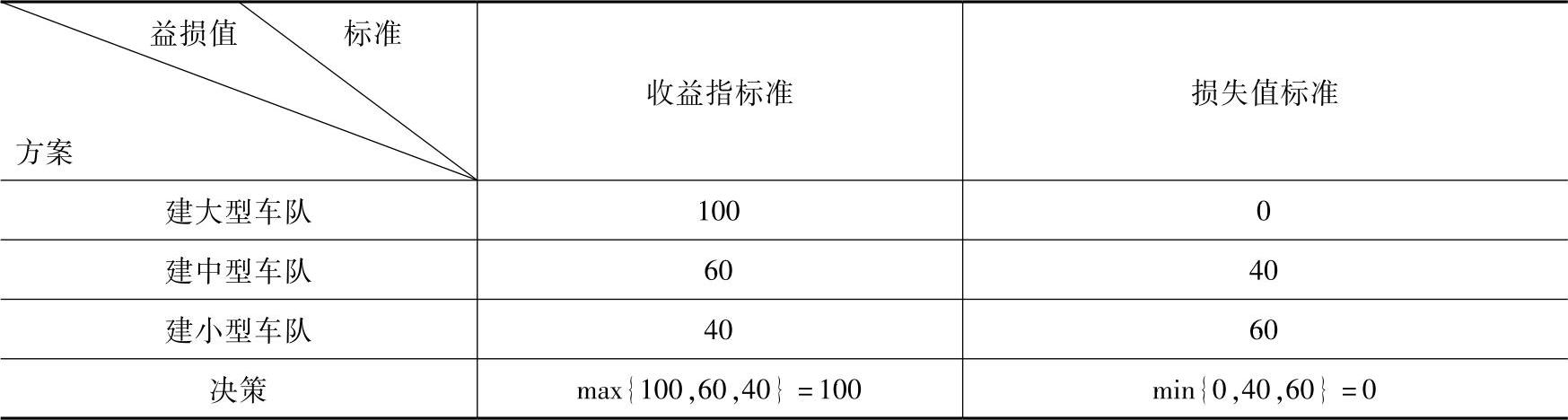
故仍然选择组建大型车队的方案。
这种决策方法适用于某一个状态的概率值相差大的情况，如果各种状态的概率值相差不大的时候，就不能用这种算法。否则，会造成决策失误。
[案例4] 某汽车客运公司经营某一旅游线路，每一班车平均获利润800元，每一班车成本800元，如果停开一班车则损失300元，现要求根据市场状况做出客运班车计划，使其获利润最多。
解：
根据上一年同期开车量资料迸行统计分析，确定不同日开车量的概率见表10-9。
1.用收益表法计算
1）根据每天可能的开车量，编制不同生产方案的收益矩阵表，见表10-10。
表10-9 开车班数及概率
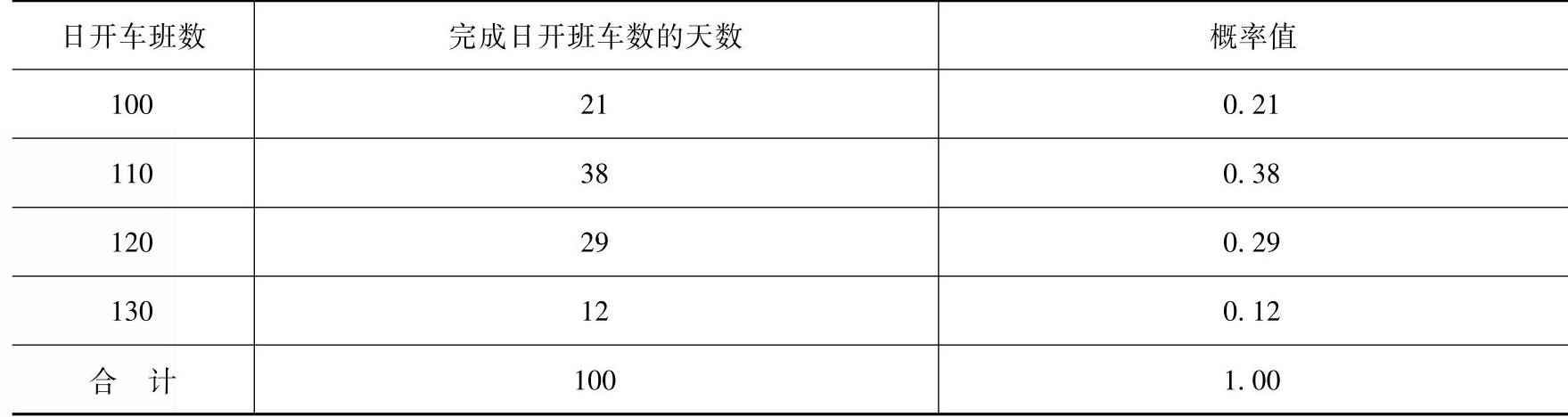
表10-10收益矩阵表
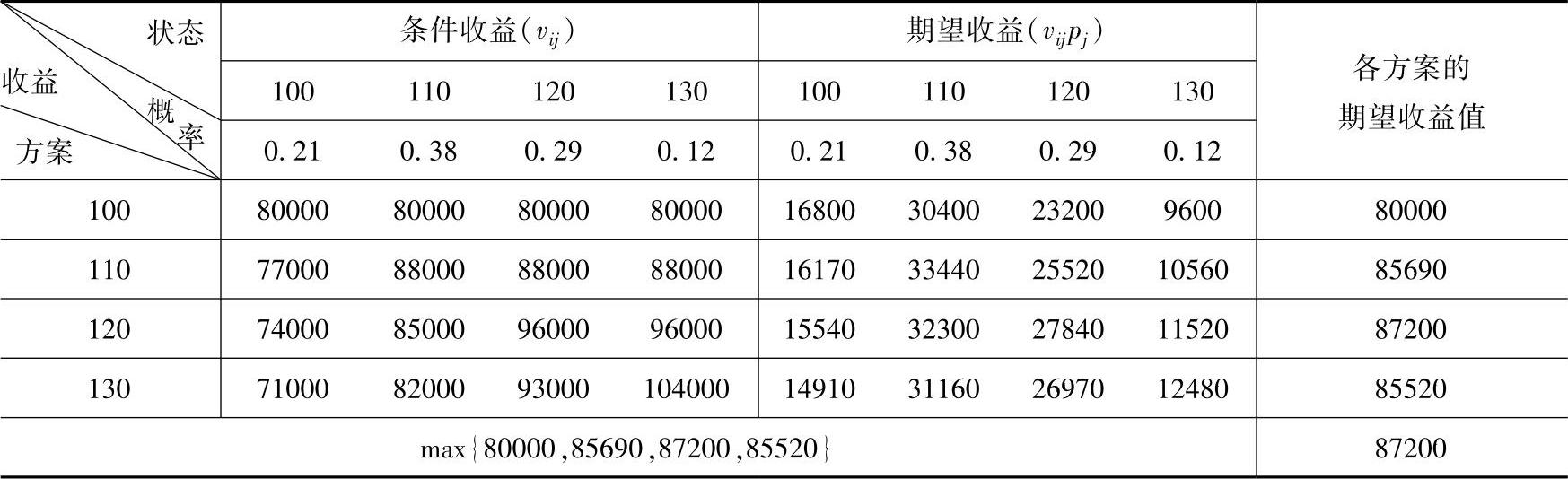
其中，条件收益值计算如下：
表内计划开车100班，当日按运输市场需求实开100班，则当日获利
v11=100×800=80000（元）
表内计划开车110班，当日按运输市场需求实开100班，剩余10班，每班损失300元，则当日获利
v11=100×800-10×300=77000（元）
依此类推，可以计算出条件收益值vij（i=1，2，3，4；j=1，2，3，4），见表10-10。
2）计算期望收益值
E（vi）=vijpj（sj）
即E（v1）=80000×0.21+80000×0.38+80000×0.29+80000×0.12=80000（元）
E（v2）=77000×0.21+88000×0.38+8800×0.29+88000×0.12=85690（元）
E（v3）=74000×0.21+85000×0.38+96000×0.29+96000×0.12=87200（元）
E（v4）=71000×0.21+82000×0.38+93000×0.29+104000×0.12=85520（元）
3）方案决策。根据上述计算可得出结论：日开班120班时，为最优方案，此时期望收益值为87200元，利润最高。
2.用期望损失表法计算
1）根据每天可能的开车量，编制不同生产方案的机会损失矩阵表，见表10-11。
用表10-11中条件收益部分每一列的最大值减去该列各值，得到的差值即为各方案在各种状态下的机会损失值。
例如，当自然状态为100班，方案为100班时，当日的条件机会损失为
v11=80000-80000=0（元）
当自然状态为100班，方案为110班时，当日的条件机会损失为
v12=80000-77000=3000（元）
当自然状态为100班，方案为120班时，当日的条件机会损失为
v13=80000-74000=6000（元）
当自然状态为100班，方案为130班时，当日的条件机会损失为
v14=80000-71000=9000（元）
依此类推，可以计算出条件机会损失值vij（i=1，2，3，4；j=1，2，3，4），见表10-11。
由表10-11可知，当日市场需要量与开车量相同，则条件机会损失值为0，所以在表10-11中，主对角线上的元素均为0。对角线以下的值是每日开车量多于每日市场需求量造成的“过剩损失”；而对角线以上的值是每日开车量少于每日市场需求量而产生的“不足损失”。
2）计算期望值机会损失值。期望值机会损失值等于条件机会损失值乘以相应的概率值。例如，自然状态为100，方案为110的期望机会损失值为
3000×0.21=630（元）
依此类推，可以计算出其他方案的期望机会损失值，见表10-11最右一列数据。
表10-11机会损失矩阵表
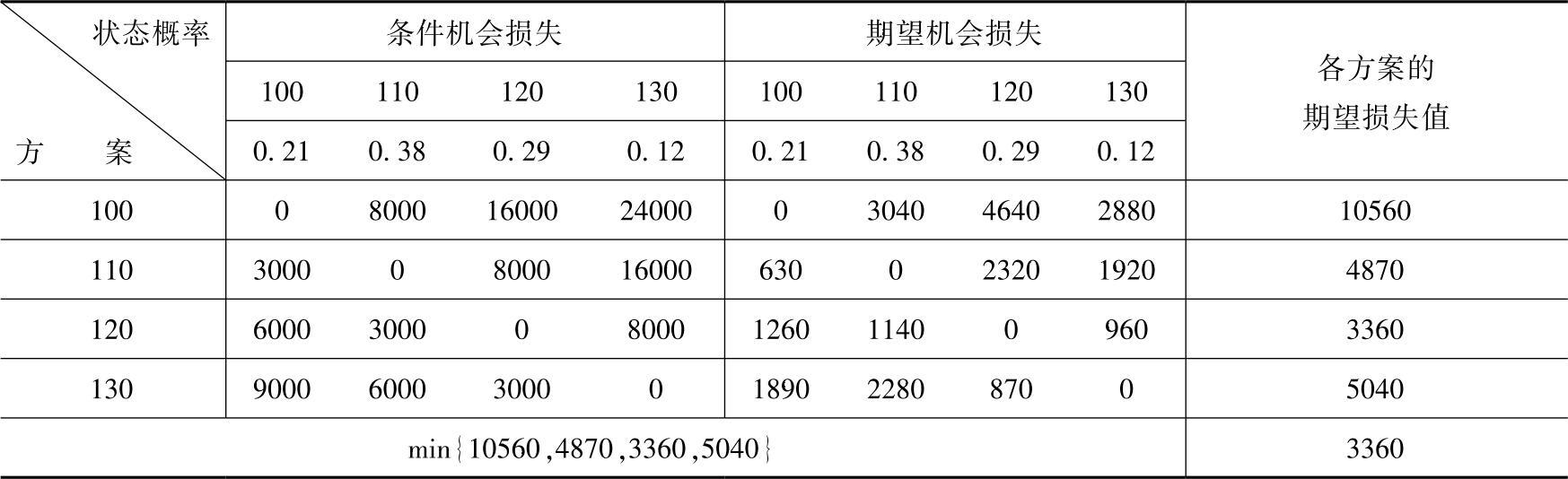
3）方案决策。
从表10-11可知，在各方案的全部机会损失中，以3360元为最小。故可做出决策：每日开班120辆车，此时的损失值最小。
用收益表法计算与用机会损失值表法得出结论是一致的，均是日发车120班为最优方案。
有关系统工程学及应用的文章
- 详细阅读
-
展成磨削法的方法的分析介绍详细阅读
常见有以下几种磨削方法。采用15°/ 20°磨削法磨削齿轮，齿面上是网状纹，它对齿面润滑有利；采用0°磨削法可对被磨齿轮的齿形进行修正及磨削鼓形齿。图16-2 双片蝶形砂轮磨齿方法a)15°/20°磨削法 b)0°磨削法2)采用钢带基圆盘展成和分度盘分度，磨削齿轮精度高。2)磨头往复运动有冲击，影响加工质量，磨削齿轮精度较前一种磨削方法低。2)展成运动和分度运动是连续的，因此生产率很高。......
2023-06-28
-
情景分析预测法的优化方法详细阅读
情景分析预测法就是在长期预测时，能够辨识关键因素及其影响方法。情景分析预测法具体有未来分析法、目标展开法和间隙分析法。图6-7 情景预测法的工作步骤[案例] 用情景预测分析法预测我国GDP发展趋势1.确定主题预测国内生产总值发展趋势。因为2006年与2005年相比，增长速度为23.9%，故以此作为情景A，对此迸行运算，可得2007年国内生产总值的预测值。......
2023-07-15
-
药剂还原法优化技巧介绍，详细阅读
向废水中投加还原剂，使废水中的有毒有害物质转变为无毒的或毒性小的新物质的方法称为还原法。本节以含铬废水为例介绍药剂还原法在废水处理中的应用。......
2023-06-19
-
冲突分析程序的优化方案介绍详细阅读
冲突分析的一般过程或程序包括以下几个主要步骤：1.对冲突事件背景的认识与描述这一阶段的工作以对事件有关背景材料的收集和整理为基本内容。4）有关各方参与冲突的动机、目的和基本的价值判断。5）各方在冲突事态中可能独立采取的行动。图10-9 冲突分析过程或程序......
2023-07-15
-
正弦条件下功率分析法的优化详细阅读
UIsinφsin2ωt部分是一个2倍系统频率的纯振荡分量，其峰值为UIsinφ。由上述瞬时功率表达式可知，对于单相正弦交流电力系统而言，其瞬时功率并不是恒定的，主要是在直流分量UIcosφ的基础上叠加了一个2倍系统频率的功率振荡分量。传统有功功率的定义为瞬时功率在一个正弦周期内的平均值。该物理量可被理解为用来表示在单位功率因数下可达到的最大有功功率。图2-1 功率三角形图2-1 功率三角形......
2023-06-23
-
电容元件的分析介绍，电容的介绍详细阅读
如果选择电压u和电流i为关联参考方向，如图3.8所示，则这个电流为图3.8电容元件图3.8电容元件电容器的电容量或耐压值不满足需要时，可以将一些电容器适当连接起来满足需要。......
2023-06-24
-
出版广告发布与行为准则的介绍详细阅读
（一）广告发布的基本原则第一，广告必须真实。（二）出版广告发布的具体行为准则有关出版广告发布的具体行为准则，可参照 《广告法》对在各种广告中所做的必须禁止的行为规定。具体而言，《广告法》第7条规定，广告内容应当有利于人民的身心健康，促进商品和服务质量的提高，保护消费者的合法权益，遵守社会公德和职业道德，维护国家的尊严和利益。......
2023-07-23
相关推荐