层次分析法：定性与定量相结合的系统分析方法

2023-07-15 理论教育版权反馈

【摘要】：层次分析法是一种能将定性分析与定量分析相结合的系统分析方法。

层次分析法（简称AHP法）是一种能将定性分析与定量分析相结合的系统分析方法。在进行系统分析时，有些问题难以、甚至根本不可能建立数学模型进行定量分析；也可能由于时间紧迫，对有些问题还来不及进行过细的定量分析，只需作出初步的选择和大致的判断就行了。这时若应用AHP方法进行分析，就可以简便而迅速地解决问题。

AHP是一种分析多目标、多准则的复杂大系统的有力工具。它具有思路清晰、方法简便、适用面广、系统性强等特点，便于普及推广，可成为人们工作和生活中思考问题、解决问题的一种方法，巨最适宜于解决那些难以完全用定量方法进行分析的决策问题。

AHP法作为一种决策方法是在1982年11月召开的中美能源、资源、环境学术会议上，由Saaty学生H.Gholamnezhad首先向中国介绍的。以后层次分析法在中国得到很大发展，很快应用到能源系统分析、城市规划和经济管理科研成果评价等许多领域中。

9.5.3.1 层次分析法原理

1.层次分析法概述

AHP法的基本思想：先按问题的要求建立起一个描述系统功能或特征的系统递阶层次结构，给出判断标度（或评价标准），对每一层的系统要素（如目标、准则、方案），进行两两比较，建立判断矩阵。通过判断矩阵特征向量的计算，得出该层要素对上一层要素的权重。在此基础上，计算出各层要素对于总体目标的综合权重，从而得出不同方案的综合评价值，为选择最优方案提供依据。

AHP法的特点：分析思路清晰，可将分析人员的思维过程系统化、数学化和模型化；分析时所需要的数据量不多，但要求对问题所包含的要素及其相关关系非常清楚、明确。

2.层次分析法的基本原理

用层次分析法进行系统分析，首先要把问题层次化，然后将因素按不同层次聚集组合，形成一个多层次的分析结构模型，如图9-8和图9-9所示。其中：

①最高层：目标层，表示解决问题的目的和要达到的总目标。

②中间层：准则层和指标层。表示采取某一方案来实现预定总目标所涉及的中间环节。

③最低层：方案层。表示要选用的解决问题的措施、策略、方案等。

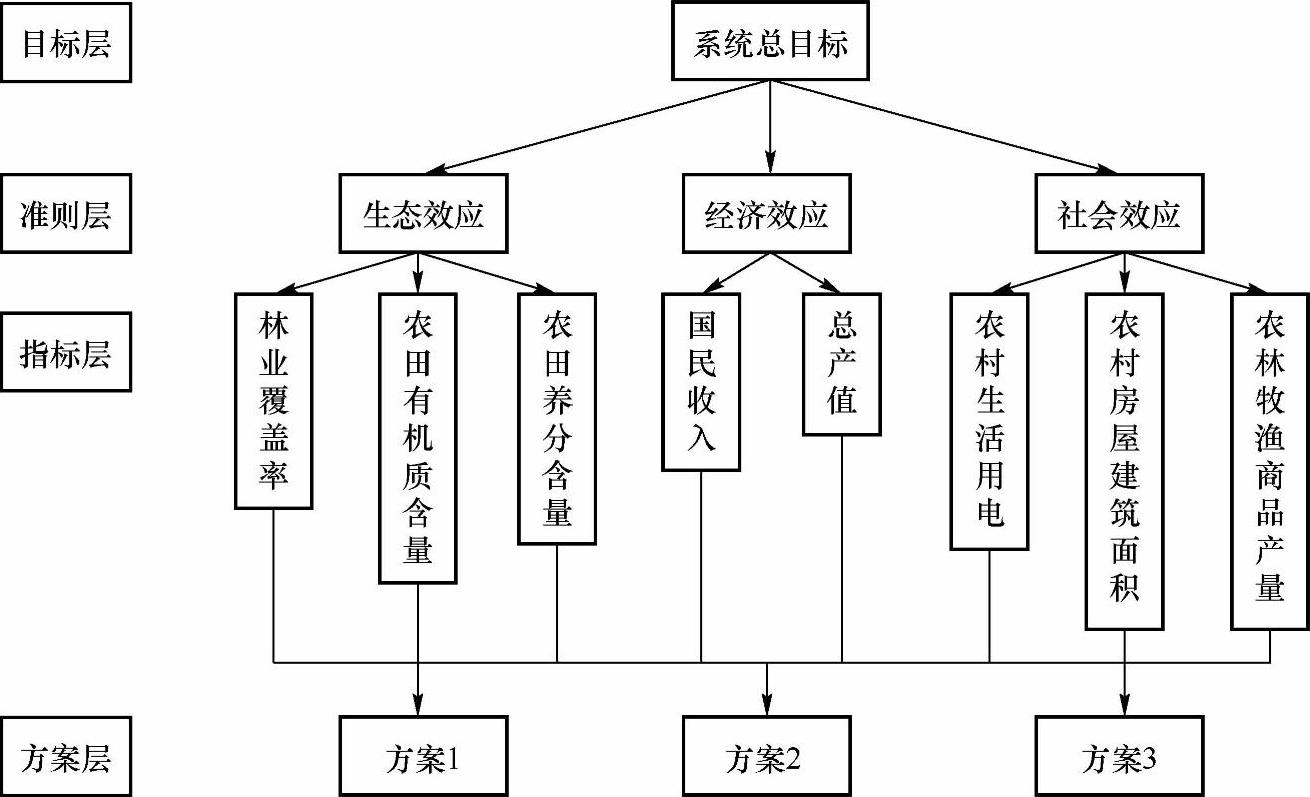
图9-8 发展农业生产方案比较层次分析给构图

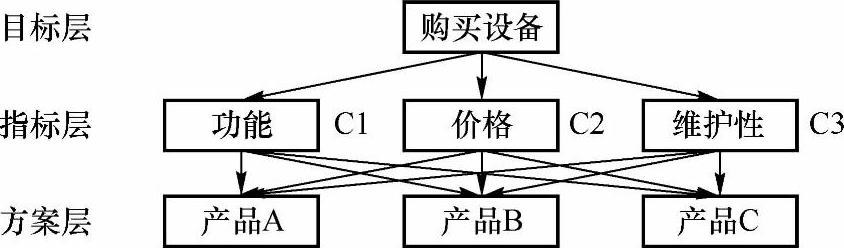
图9-9 购买设备方案层次分析给构图

3.层次分析法中的排序——特征向量法

人们在日常生活中经常要从一堆同样大小的物品中挑选出最重的物品。这时，人们总是利用两两比较的方法来达到目的。假设有n个物品其真实重量为ω₁，ω₂，…，ω_n，如果人们可以精确地判断两两物品之重量比，那么就可以得到一个重量比矩阵A

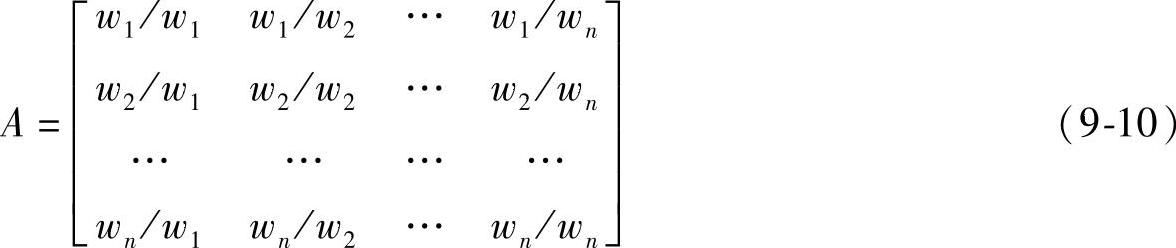
如果用矩阵A左乘物品重量向量W=[ω₁ω₂…ω_n]^T，则有

注意到上式n是A的特征值，W是A特征向量。这就提示我们利用求重量比判断矩阵之特征向量的方法来求得物品真实的重量向量W。如果A是精确比值矩阵，则其特征值λ_max=n，即AW=λW。但一般情况下A是近似估值，故有λ_max≥n，因此可以用λ_max与n的误差来判断A的准确性。

4.层次分析法的基本步骤

应用层次分析法进行系统评价，其主要步骤有：

1）对构成评价系统的目的、评价指标（准则）及替代方案等要素建立多级递阶的结构模型。

2）对同属一级的要素以上一级的要素为准则进行两两比较，根据评价尺度确定其相对重要度，据此建立判断矩阵。

3）计算判断矩阵的特征向量以确定各要素的相对重要度。

4）最后通过综合重要度的计算，对各种方案要素进行排序，从而为决策提供依据。

5.层次分析法中的判断矩阵

判断矩阵是层次分析法的基本信息，也是进行相对重要度计算的重要依据。如上所述，判断矩阵A中元素a_ij表示i元素与j元素相对重要度之比，巨有下述关系（即为反对称阵）

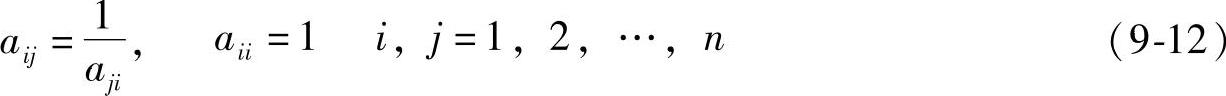
显然比值越大，则i的重要度就髙。为了方便，一般采用这样的尺度，规定用1、3、5、7、9分别表示i元素与j元素同样、比较重要、重要、很重要、极重要。当然也可以根据实际需要取其他值。

[案例1] 为购买机器，选定的三个评价标准为功能C₁、价格C₂和维护性C₃。假定以购买机器为比较基准，对这三个指标两两比较的结果见表9-14。

表9-14 购买机器比较矩阵

上述矩阵C₃×3表明，对购买机器而言，功能比价格重要（C₁₂=5）、比维护性较重要（C₁₃=3），而维护性比价格较重要（C₃₂=3），其他可以类推。

9.5.3.2 层次分析法的计算过程

1.相对重要程度的计算

理论上讲，对以某个上级要素为准则所评价的同级要素之相对重要程度可以由计算比较矩阵A或C的特征向量获得。但因计算方法较复杂，而巨实际上只能获得对A或C粗略的估计。实际中可以采用几何平均法和规范几何法来计算比较矩阵的特征向量。

（1）几何平均法或称求根法

①将矩阵按行求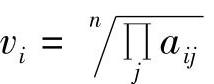

②归一化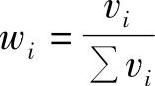，i=1，2，…，n

③W=[ω₁ω₂…ω_n]^T即为所求的特征向量。

（2）规范列几何法或称求和法

①将矩阵按列规范化或归一化

②按行求和

③求平均值

④W=[ω₁ω₂…ω_n]^T即为所求特征向量。

2.计算判断矩阵的最大特征根λmax

式中，（AW）_i是向量AW的第i个元素。

[案例2] 用几何平均法计算下列判断矩阵A的最大特征值和相应的特征向量。

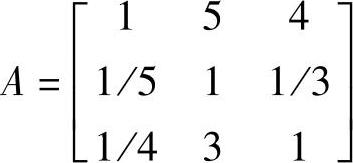
解：

①将矩阵按行求根

②归一化

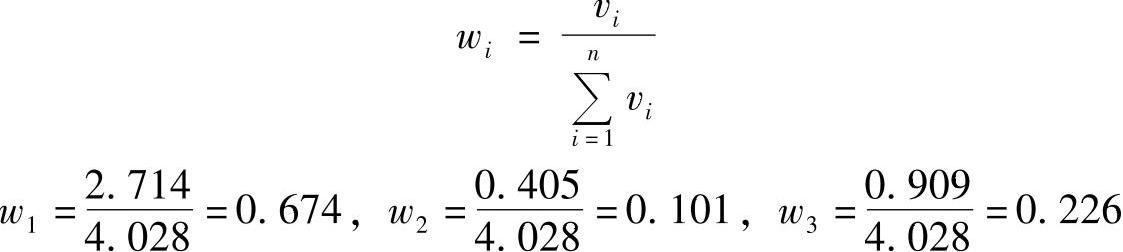
③计算A的最大特征值λmax

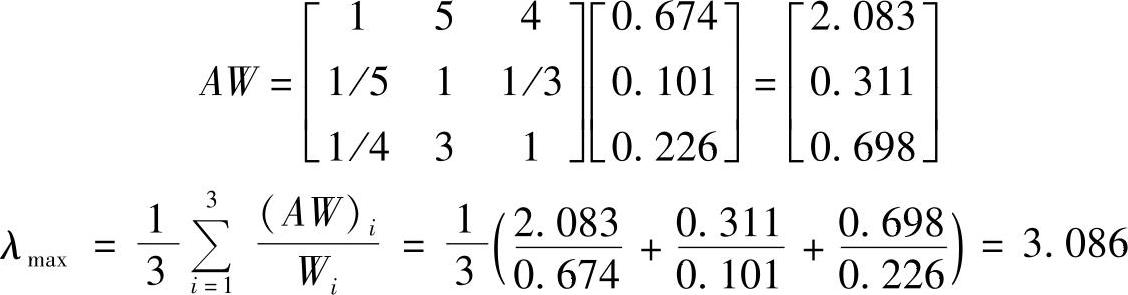
[案例3] 用规范平均法计算同[案例2]一样的判断矩阵A的最大特征值和相应的特征向量。

解：

①将矩阵按列规范化

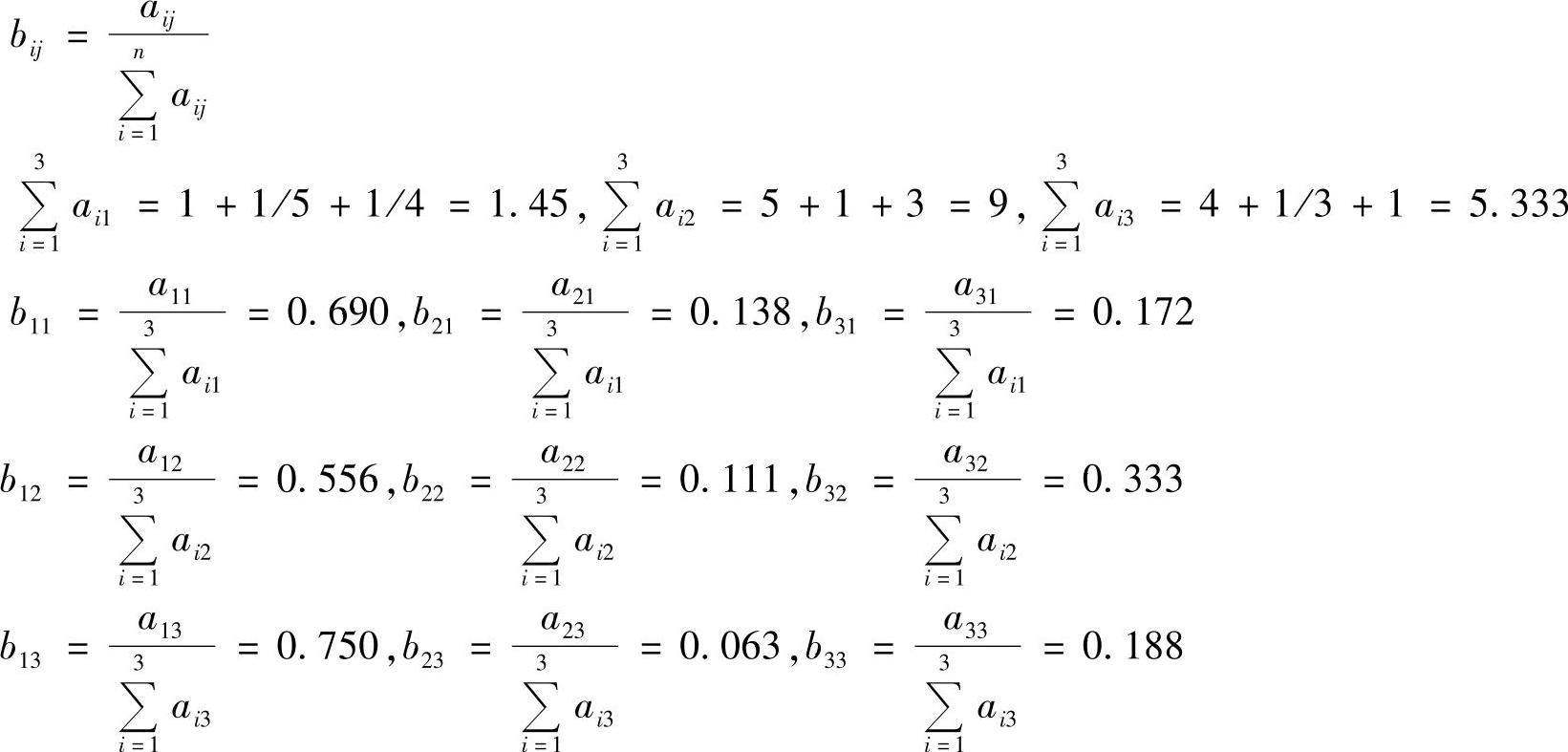
规范化后的矩阵

②按行求和并平均

W=[0.6590.1040.231]^T即为所求的特征向量。

③计算最大特征值λmax

④两种方法计算结果比较

几何平均法

W=[0.6740.1010.226]^T，λ_max=3.086。

规范列平均法

W=[0.6590.1040.231]^T，λ_max=3.089。

由此可见，这两种方法的特征值计算结果几乎一样，特征向量计算结果略有差别。

3.单层次排序的一致性检验

在实际评价中评价者只能对A进行粗略判断，甚至有时会犯不一致的错误。为了检验判断矩阵的一致性（相容性），根据AHP原理，利用λ_max与n之差检验一致性。

（1）计算一致性指标CI

（2）计算平均随机一致性指标CR

随着n的增加，判断误差就会增加。因此，判断一致性应当考虑到n的影响，需要使用一致性比值CR。公式（9-18）中的RI为平均随机一致性指标，表9-15是500个样本计算得到的评价指标RI。

表9-15 平均随机一致性指标RI

当CR<0.1时，认为判断矩阵具有满意的一致性，否则需要调整判断矩阵，直到具有满意的一致性为止。

4.层次总排序或综合重要度的计算

在分层获得了同层各要素之间的相对重要程度后，就可以自上而下地计算各级要素关于总体的综合重要度。设c级有m个要素c₁，c₂，…，c_m，其对总值的重要度为ω₁，ω₂，…，ω_m；它的下级有n个要素P₁，P₂，…，P_n，P_i关于c_j的相对重要度为v_ij，则P级的要素P_i的综合重要度为

其计算过程见表9-16。

表9-16 综合重要度

5.层次总排序的一致性检验

这一步骤同样是从高到低、逐层进行的。如果B层某些元素对于层A中的A_j单排序的一致性指标为CI_j，相应的平均随机一致性指标为RI_j，则层次总排序一致性比值为

当CR<0.1时，认为层次总排序结果是满意的。

[案例4] 某市是以煤炭工业为主的老工业城市，近年来，工农业总产值持续稳定增长，但随着生产的发展，运输缺口也越来越大，已成为经济进一步发展的主要障碍，急需投资交通工程项目，以扩大运输能力。该项目有三个备选方案：水运、公路运输、铁路运输，试用层次分析法对优先发展的运输方案作一排序。

解：

1）分析该运输系统的要素集合及相关关系，用结构分析法建立系统的层次结构模型如图9-10所示。

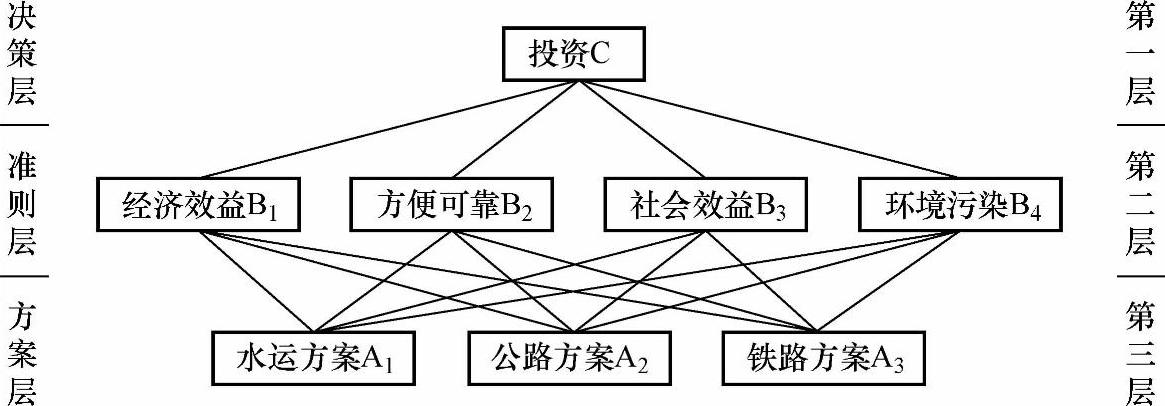
图9-10 系统的层次给构模型

2）确定评价基准或判断标度。定义判断标度见表9-17。

表9-17 定义判断标度

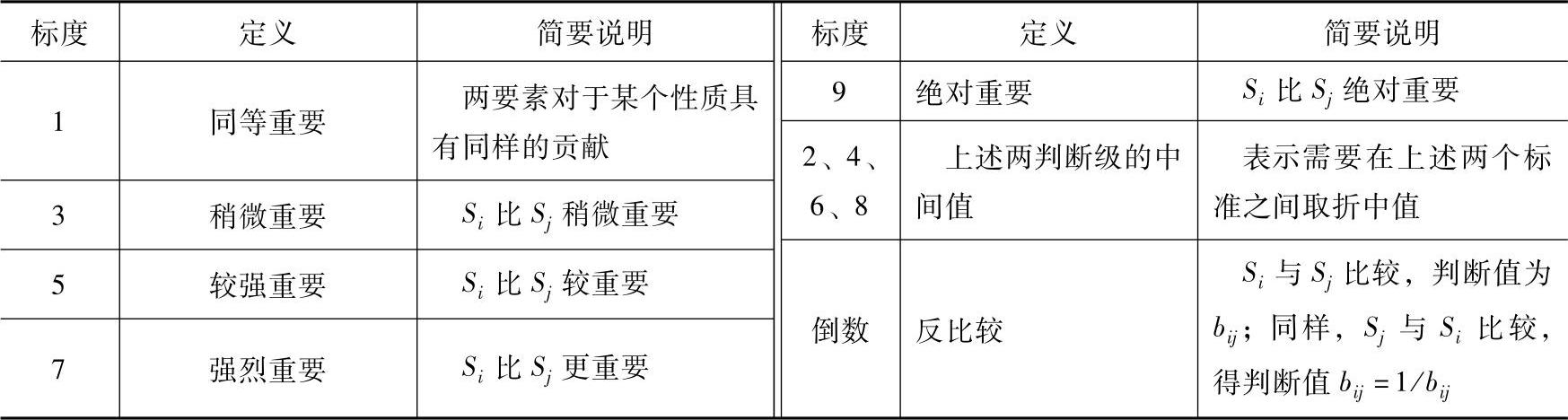
3）从最上层要素开始，依次以最上层要素为依据，对下一层要素两两比较，建立判断矩阵。

①先以第一层要素（投资层）为依据，对第二层（准则层）要素建立判断矩阵见表9-18。

②再以第二层要素（准则层）为依据，对第三层（方案层）要素建立判断矩阵。由于此时有四个准则，故有四个判断矩阵，见表9-19、表9-20、表9-21、表9-22：

表9-18 判断矩阵（1）

表9-19 判断矩阵（2）

表9-20 判断矩阵（3）

表9-21 判断矩阵（4）

表9-22 判断矩阵（5）

4）根据判断矩阵，计算各要素的优先级向量。

①首先计算表9-18判断矩阵各要素的优先级向量。由于此时判断矩阵为4×4矩阵，则首先计算矩阵各行元素乘积的4次根

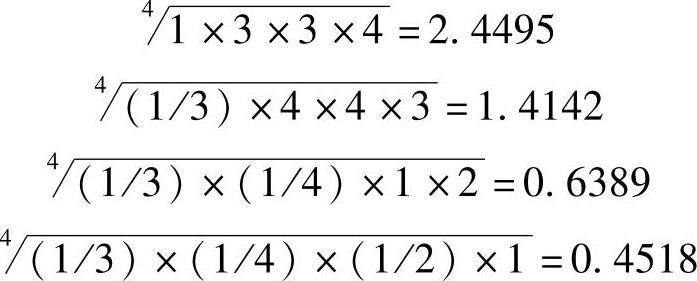
②将上述计算结果归一化。即将上述各数相加，得到一个总数。然后对每一个数都除以这个总数。这样就得到了表9-19中各要素B₁、B₂、B₃、B₄的优先级向量。过程如下

2.4495+1.4142+0.6389+0.4518=4.9544

2.4495/4.9544=0.4944

1.4142/4.9544=0.2854

0.6389/4.9544=0.1290

0.4518/4.9544=0.0912

故以投资为准则时，经济效益、方便可靠、社会效益、环境污染的优先级向量为

（0.4944，0.2854，0.1290，0.0912），将此优先级向量写在表9-19的最后一列。

依次方法，可求出其他几个矩阵的优先级向量，如各表最后一列所示。

5）确定总体优先级向量。总体优先级向量的计算见表9-23。

表9-23 总体优先级向量

总体优先级向量的计算如下

0.4944×0.0719+0.2854×0.6483+0.1290×0.5400+0.0912×0.6483=0.3493

0.4944×0.6491+0.2854×0.1220+0.1290×0.2970+0.0912×0.2297=0.4150

0.4944×0.2790+0.2854×0.2297+0.1290×0.1633+0.0912×0.1220=0.2357

6）按照优先级别向量，对系统进行分析、评价、排序。

根据总体优先级向量可知，水运方案的总体优先级为0.3493，公路方案的总体优先级为0.4150，铁路方案的总体优先级为0.2357，可以认为三个方案的排序应为A₂、A₁、A₃，即应选择公路方案。

7）判断矩阵一致性检验。以此例中方便可靠准则B₂对三个运输方案建立的判断矩阵的最大特征根及一致性检验为例，计算过程如下

由

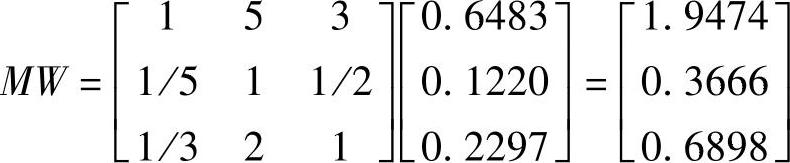
得该判断矩阵的最大特征根为

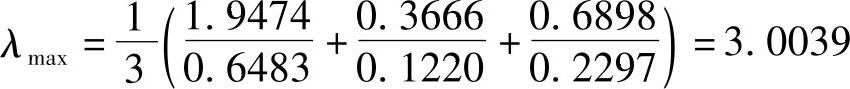
则

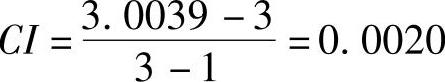
且

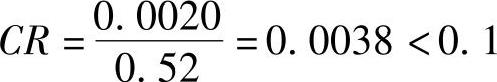
故认为准则B₂对三个运输方案建立的判断矩阵的一致性较好，是可以接受的。

同样，可求得其余几个判断矩阵的最大特征根，并经过一致性检验后，认为其余几个判断矩阵的一致性也较好，也是可以接受的。

9.5.3.3 层次分析法的特点

1.系统性

层次分析法把研究对象看作一个系统，按照分解、比较判断、综合的思维方式进行决策，成为继机理分析、统计分析之后发展起来的系统分析的重要工具。

2.实用性

层次分析法把定性和定量方法结合起来，能处理许多用传统的最优化技术无法着手的实际问题，应用范围很广。同时，这种方法使得决策者与决策分析者能够相互沟通，决策者甚至可以直接应用它，这就增加了决策的有效性。

3.简洁性

步骤简单，计算也方便，巨所得结果简单明确，容易被决策者了解和掌握。

4.局限性

首先该方法只能从原有的方案中优选一个出来，没有办法得出更好的新方案。其次，该方法中的比较、判断以及结果的计算过程都是粗糙的，不适用于精度较高的问题。另外，从建立层次结构模型到给出成对比较矩阵，人的主观因素对整个过程的影响很大，这就使得结果难以让所有的决策者接受。当然采取专家群体判断的办法是克服这个缺点的一种有效途径。

层次分析法：定性与定量相结合的系统分析方法

相关推荐