根据不同标准,教学评价可以区分出不同的类型。在教学评价中应重视二者的结合。......
2023-11-03
关联矩阵(relevance matrix)是常用的综合评价方法。设有A1,A2,…,Am是某评价对象的m个替代方案。x1,x2,…,xn是评价替代方案的n个评价指标。ω1,ω2,…,ωn是n个评价指标的权重。vi1,vi2,…,vin是第i个替代方案Ai的关于xj指标(j=1,2,…,n)的价值评定量,相应的关联矩阵表见表9-7。
表9-7 关联矩阵表

应用关联矩阵评价方法的关键,在于确定各评价指标的相对重要度,即权重ωi以及由评价主体给定的评价指标的评价尺度。目前国内外应用比较广泛的确定权重及评价尺度的方法是逐对比较法和古林法(A.J.Klee)。下面对这两种方法逐一介绍。
1.逐对比较法
利用多元评价指标对替代方案进行综合评价时,最简便的方法就是逐对比较法。逐对比较法就是利用所有评价指标对替代方案按照一定的基准进行评分,再利用加权的方法对替代方案的各种评价指标的评价值进行综合的评价方法。下面以交通安全对策为例,介绍逐对比较法在确定权重及评价尺度上的应用。
假定综合评价某地为减少交通事故制定的三种措施(设置防事故栅栏、设置人行道和设置交通信号,并分别用A1、A2和A3表示),评价指标有5个:分别为死亡者的减少、负伤者的减少、经济损失的减少、外观以及实施的费用。这里首先对表9-8的所有评价指标进行两指标间重要程度的判定。判定为更重要的指标给1分,相对应的另一个就为不重要的指标给0分,把各个评价指标的得分相加,归一化(即所有指标评分的合计值为1)后即得各指标的权重。
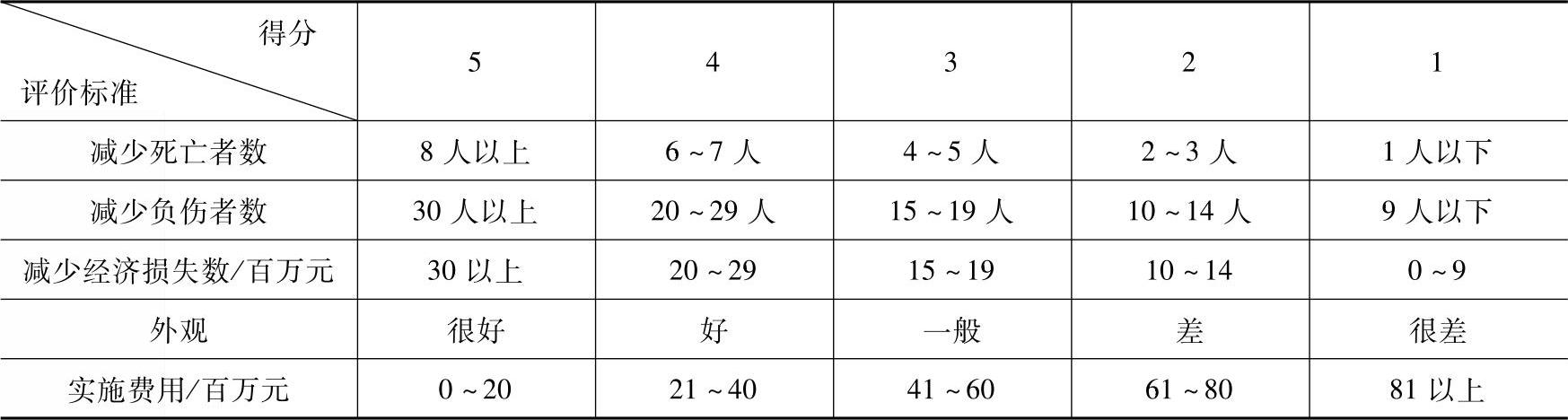
现在,对三个方案进行比较,它们的使用效果见表9-9。所设得分计算基准见表9-10,则各替代方案的综合得分值vi可用下式计算。
对于方案A1——设置防事故栅栏
v1=0.4×3+0.3×2+0.1×2+0×2+0.2×5=3
对于方案A2——设置人行道
v2=0.4×4+0.3×3+0.1×3+0×5+0.2×1=3
对于方案A3——设置交通信号
v3=0.4×2+0.3×1+0.1×1+0×3+0.2×5=2.2
这样A1、A2方案有了同等的分值,属于待选方案,A3属于淘汰方案。要在A1、A2中进一步选择时,需加入新的评价因素后才能确定。
表9-8 用逐对比较法计算权重的例子
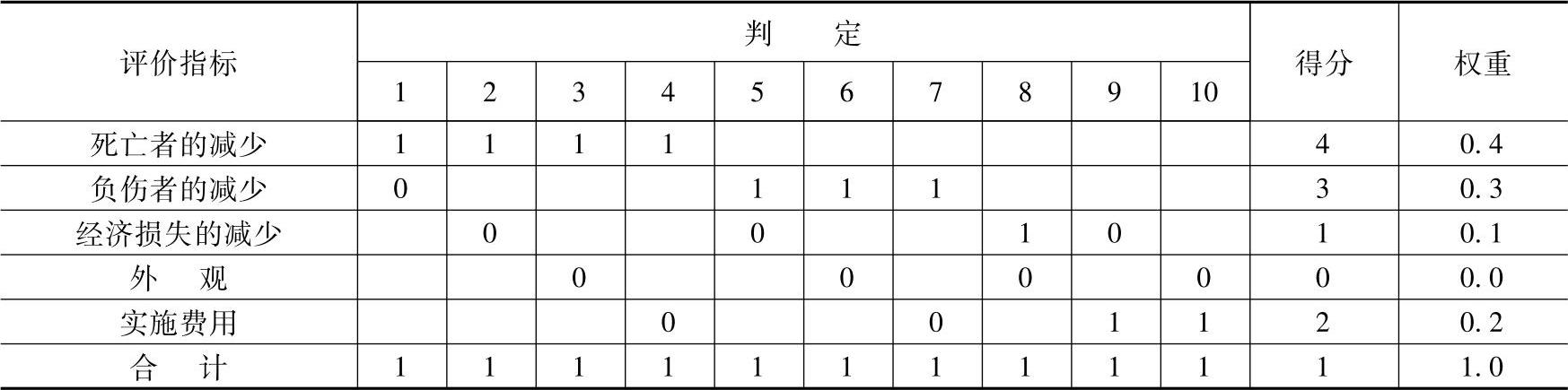
表9-9 替代方案的使用效果

表9-10 得分基准
2.古林法(A.J.Klee)
当指标之间的重要性可以在数量上作出判断时,可以采用古林法确定权重及评价尺度。工作步骤如下:
1)把评价指标以任意顺序排成一列。
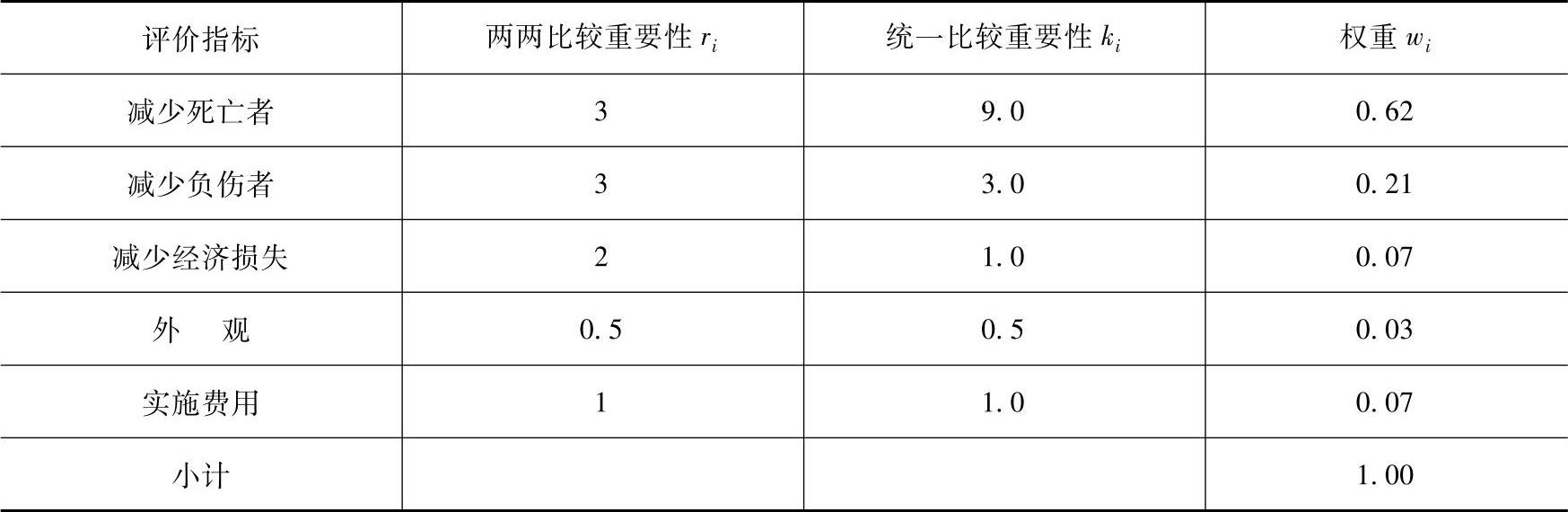
2)从下到上对相邻的评价指标进行两两评价。评价时,以下面指标为基准,在数量上进行重要度的判定(ri栏)。在表9-11中,外观的重要性是实施费用的0.5倍,经济损失减少的重要性是外观的2倍,负伤者减少的重要性又是经济损失的3倍,死亡者减少的重要性是负伤者减少的3倍。
3)基准化。把实施费用的重要性ri设为1,按照从下而上的顺序乘以ri,就得到统一比较重要性ki列。
4)归一化ki列,使该列的合计值为1,即得到各评价指标的权重ωi。
表9-11 古林法确定权重
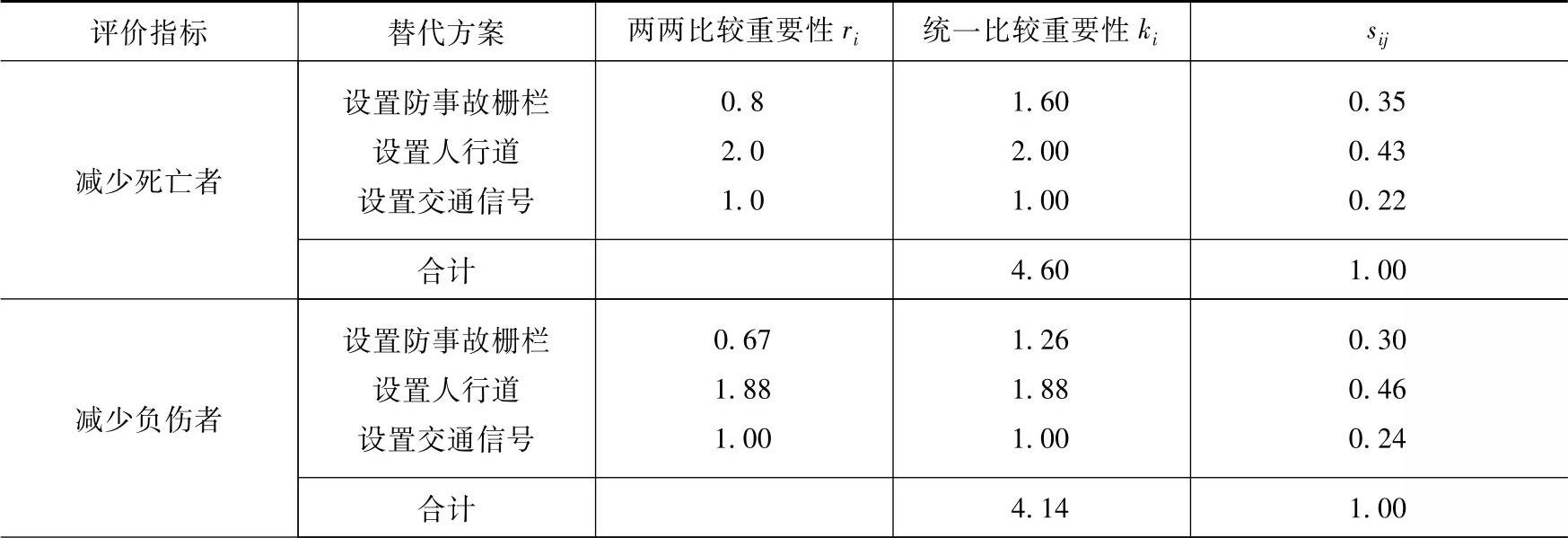
接着用以上5个评价指标对替代方案进行评价,计算结果见表9-12。该表给出了ri、ki和sij的计算过程。
最后计算出三个方案的综合评价得分。计算公式为

计算结果见表9-13。由该表可知,设置人行道这个方案是最佳方案。
表9-12 按评价指标对各替代方案的评价①
(续)

① 汪应洛.系统工程理论、方法与应用(第二版).高等教育出版社,1998
表9-13 替代方案综合得分计算表

有关系统工程学及应用的文章

在教育实验评价中,对实验内在效度和外在效度等方面的评价,有利于人们了解通过实验所获得的认识的适用范围和适用程度,从而有针对性地进一步指导教育实践。要对实验的外在效度进行评价,判定实验成果的可推广范围和可推广程度,这也是实验应用价值的重要反映。......
2023-11-18

建立因子分析模型的目的不仅仅要找出公共因子以及对变量进行分组,更重要的要知道每个公共因子的意义,以便进行进一步的分析,如果每个公共因子的含义不清,则不便于进行实际背景的解释.由于因子载荷阵是不唯一的,所以应该对因子载荷阵进行旋转.目的是使因子载荷阵的结构简化,使载荷矩阵每列或行的元素平方值向0和1两级分化.有三种主要的正交旋转法:方差最大法、四次方最大法和等量最大法.(1)方差最大法方差最大法从简......
2023-11-18

关于分类和回归模型的各种评估方法,一种是处理分类任务的模型,一种是预测回归的模型,这两种模型的评估方法也不完全一致,下面就来分别介绍两种类型模型的各种评估手段。AUC可以说是用单个数字总结模型性能的最好方法,其实就是ROC曲线下方的面积大小。平均绝对误差可以避免误差相互抵消的问题,因而可以准确反映实际预测误差的大小。MAE可以表示预测与实际结果的接近程度。以上即为两种模型的常用评估方法。......
2023-11-08

定位特征是为构造新特征提供定位功能的,它包括工作平面、工作轴、工作点。可以将工作平面作为新的草图平面,也可以将它作为特征的限位面以及装配时的辅助定位面。单击“模型”选项卡中的“定位特征”选项,如图5-37所示,即可以生成工作平面等。图5-36系统默认的定位特征图5-37“定位特征”工具条1.工作平面的创建创建工作平面的方法就是根据几何知识确定平面的方法。......
2023-06-28

从数量众多的艺术美学理论成果,特别是教材编写出版情况来看,学术界对西方传统美学的研究与应用较为普遍、清晰,而对马克思主义美学中国化的理论研究及其应用,显得目标不明、思路不清。可以说,刘纲纪运用中国化的马克思主义美学理论研究并阐述中国艺术美学理论,在谢赫画论研究上达到了较为圆熟的境界,是马克思主义美学中国化及其在艺术美学领域成熟应用的杰出范例。......
2023-08-22

人格测量的主要方法有自陈量表法和投射测验法。自陈量表法自陈量表法是让被试按自己的意见,对自己的人格特质进行评价的一种方法。自陈量表通常也称为人格量表。用自陈量表法编制的人格量表,在我国常见的有明尼苏达多项人格测验量表、爱德华个人兴趣量表、卡特尔系列人格特征量表和艾森克人格类型量表等。明尼苏达多项人格测验包括10个临床量表。......
2023-11-06

观测人体运动要确定观测对象及观测坐标系。在人体运动的研究中,最常用的是直角坐标系。常用的直角坐标系有三种:一维坐标系:直线运动,沿着一个方向运动,如一百米跑、游泳等。视频跟踪法是应用视频对人体的运动进行跟踪、捕捉和分析。图3-18摄影观察法人体运动属于非刚体运动的范畴,具有高度的非线性特点。......
2023-06-21
相关推荐