首页理论教育规定总工期概率评估与优化

规定总工期概率评估与优化

2023-07-15 理论教育版权反馈

【摘要】：对于没有确定工作时间的网络计划问题，需要采用三时估计法。因此，就要对整个计划能否按规定日期完工进行概率评价。试画出该任务的网络图，找出关键线路，并进行总工期的概率评价。解答此问题可分两步走：①计算规定完工期的概率系数Z，其计算公式为为了便于查表，需将一般正态分布N转化为标准正态分布N（0，1），从而引进Z。表8-7 任务完成概率

对于没有确定工作时间的网络计划问题，需要采用三时估计法。但由于是估计就会产生一定偏差。因此，就要对整个计划能否按规定日期完工进行概率评价。对按期完工可能性低的计划重新安排，以避免盲目开工，不能按期完成预定任务，造成经济损失。

通常，大多数情况下可认为对工作完工时间的估计是符合正态分布的，因此各工作完工时间的估计偏差σ（i，j）可以用式（8-20）求出

式中，t_o是最快完工估计时间；t_P是最慢完工估计时间。

由各关键工作组成的关键线路的估计偏差，即总工期估计偏差可用式（8-21）求出

[案例] 某任务经分解、分析后，得出的明细表见表8-5。试画出该任务的网络图，找出关键线路，并进行总工期的概率评价。

表8-5 任务明细表

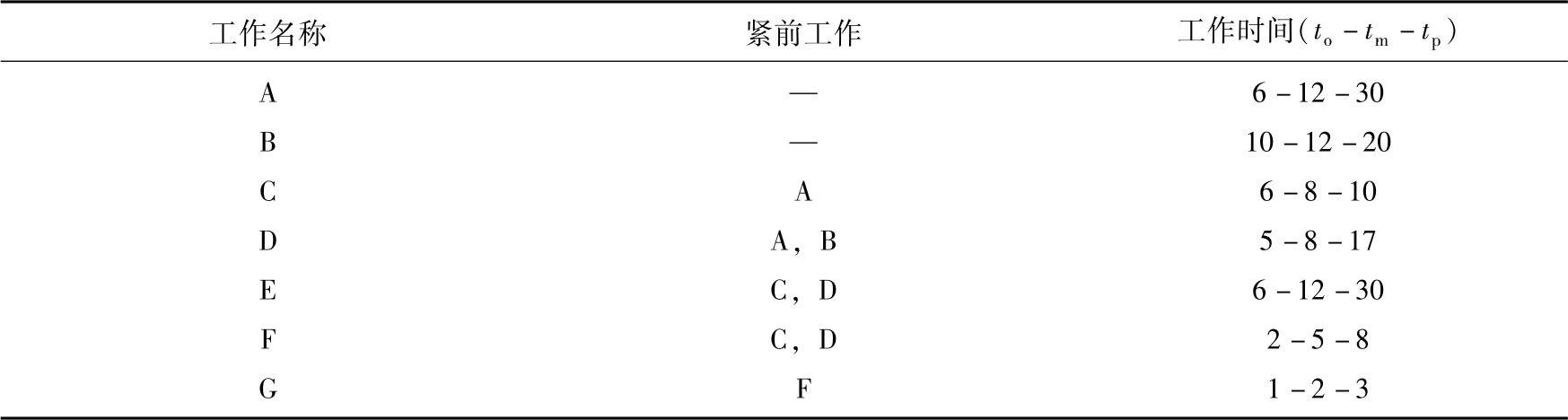
解：

根据三时估计法的计算公式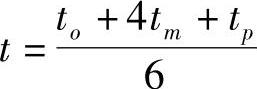，可以得出各工作的工时。再根据表8-5中列出的各工作之间的逻辑关系，画出网络图。经过事项时间参数的计算，确定出关键线路A→B→E。如图8-12所示。

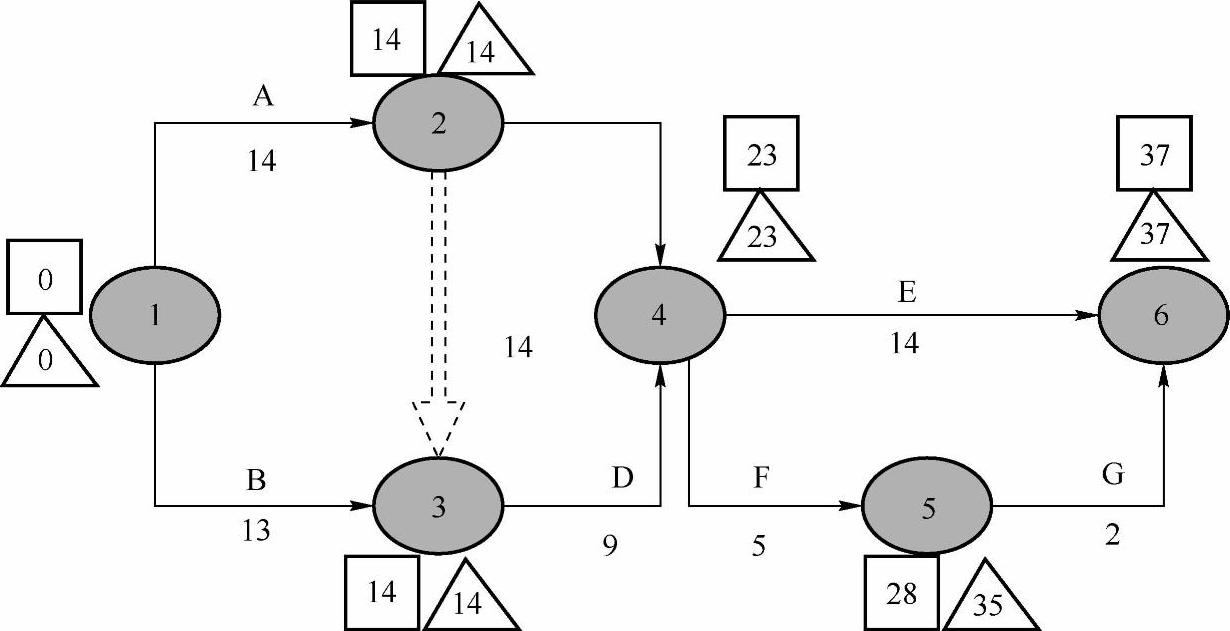
图8-12 关键线路

在图8-12中，各关键工作的估计偏差为

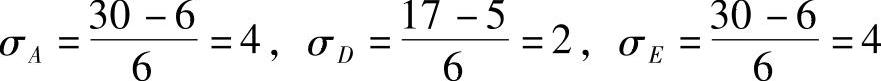
则关键线路路长值即计划工期的估计偏差为

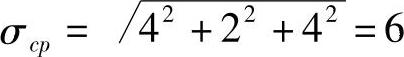
总工期概率分析与评价主要内容包括：

1.规定完工期求概率

如图8-12所示，其任务的计划完工期为37天。

如果根据客观情况，必须31天完工，则此项任务按规定时间31天完工的可能性有多少？解答此问题可分两步走：

①计算规定完工期的概率系数Z，其计算公式为

为了便于查表，需将一般正态分布N（T_e，σ²）转化为标准正态分布N（0，1），从而引进Z。把相应数值代入上述公式，得到

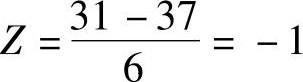
如不是对整个工期，而是对某一事项的完工进行概率评价，在确定到该事项计划工期估计偏差时，应在各条线路中选取先行工作方差累计值的最大值。如计算事项④完工期的偏差值，应该选经①→②、②→③、③→④最后到事项④的方差，即事项④的标准差为

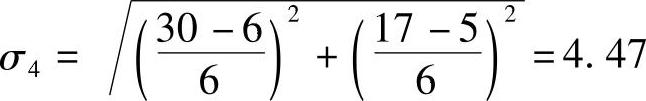
②根据概率系数，通过查表8-6，求概率。

表8-6 概率系数与概率关系

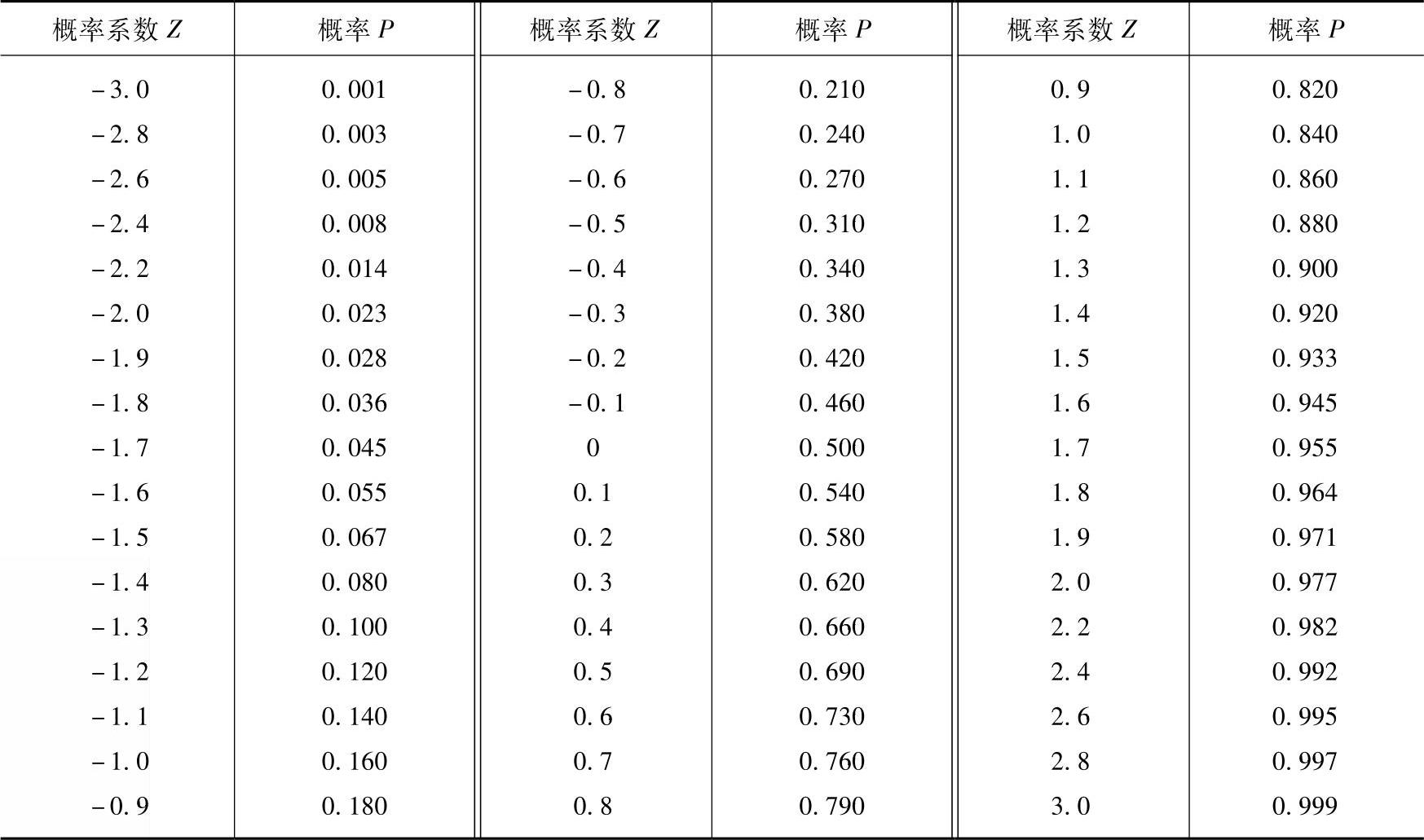
当Z=-1时，查表8-6得到P=0.16，显然完成的可能性只有16%，属于较低水平（对比表8-7）。根据制订计划既要可行，又要先进的原则，概率值在0.3<P<0.7范围内是比较合适的。当P<0.3时，风险性太大；当P>0.7时，计划完成较易，不利于激发职工的进取精神。

2.规定概率求完工期

如对项目按期完工的可能性有要求，工期应规定多少时间为宜，可由式（8-23）算出

T_s=T_e+Z×σ_cp （8-23）

[案例] 假设要求本节案例1的项目有90%的把握按期完工，规定工期为多少天合适？

解：当P=0.9时，查表8-6，可得到相应的概率系数Z=1.3，代入式（8-23），则有

T_s=37+1.3×6=44.8（天）

说明若此项目规定为44.8天时，有90%的可能性实现按期完工。

表8-7 任务完成概率