[案例]某港口为了解决产能不足的问题，计划进行扩建。该港口计划部门拟利用模拟方法，模拟该港码头计划期的船舶到港情况，以便设计合理的码头扩充方案。码头报告100天内每天到港的船舶艘数见表7-8。
表7-8 100天内每天到港的船舶艘数
解：
第一步：根据以上资料，观察船舶到港是什么样的分布。可以用直方图来表现，如图7-9所示。由图7-9可以看出，船舶到港基本上类似于泊松分布。
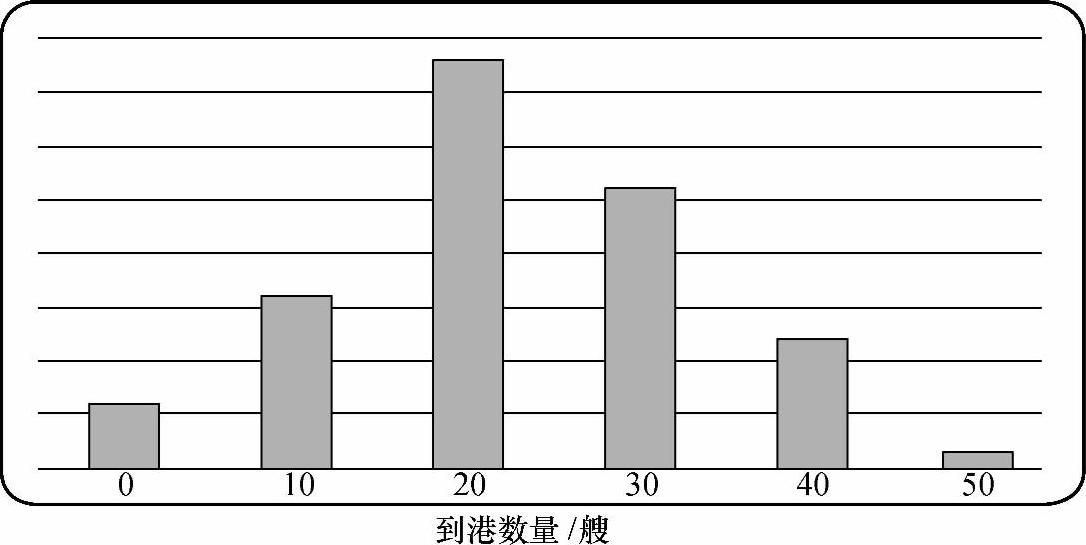
图7-9 到港艘数直方图
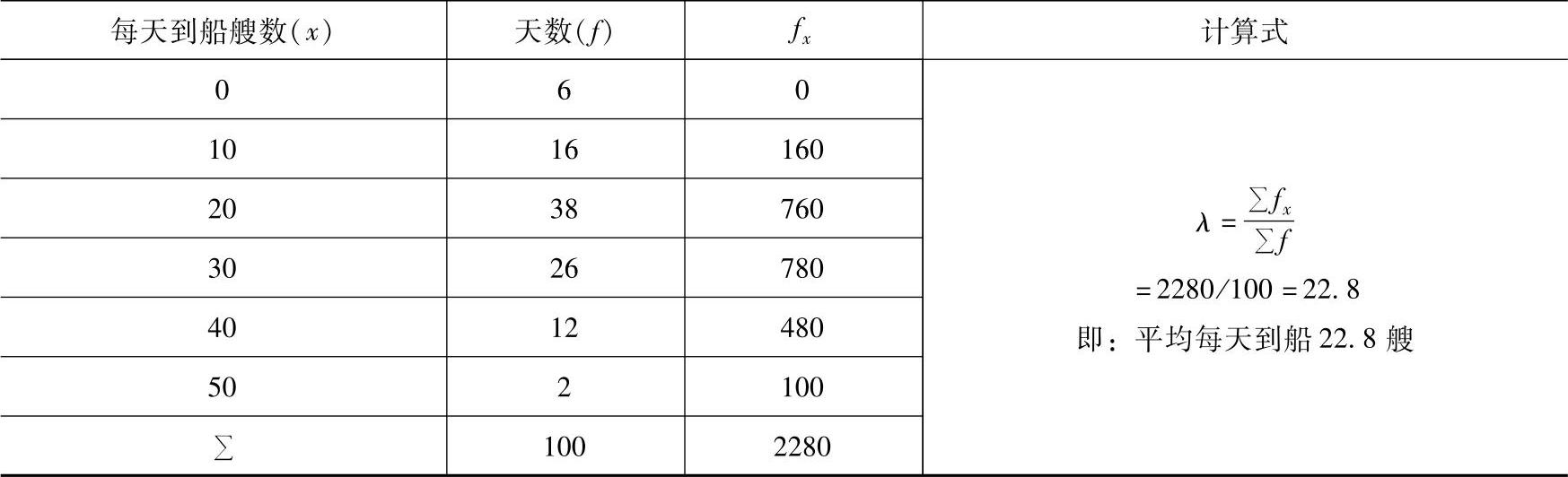
第二步：按照泊松分布公式的要求，计算它的分布参数λ。经过计算得
λ=22.8（艘）
第三步：考虑发展因素。根据题意，该外贸码头计划期平均每天到港的船舶艘数可增加5%左右，按此计算，可得：
22.8×0.05=1.14（艘）
即计划期每天到港数可增加1.14艘。因此，计划期每天到港的船舶艘数应为：
λ=22.8+1.14=23.94（艘）
第四步：求事件的随机概率
1）计算每日到港船舶艘数的理论次数分布：由于本例的先验分布基本上类似于泊松分布，因此，我们以泊松分布作为该例题的理论分布。在泊松分布的λ中，还需要考虑因求平均分布所抵消的部分，即在23.94中再增加一个1.14，得25.08≈25。取25作为计算参数λ，代入泊松公式
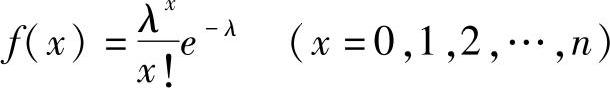
得每天平均到港0～70艘的理论次数分布见表7-9。
表7-9 每天平均到港船舶的理论分布值
2）求平均次数分布：将先验次数分布与理论次数分布相加，求平均次数分布，见表7-10。
表7-10 平均次数分布
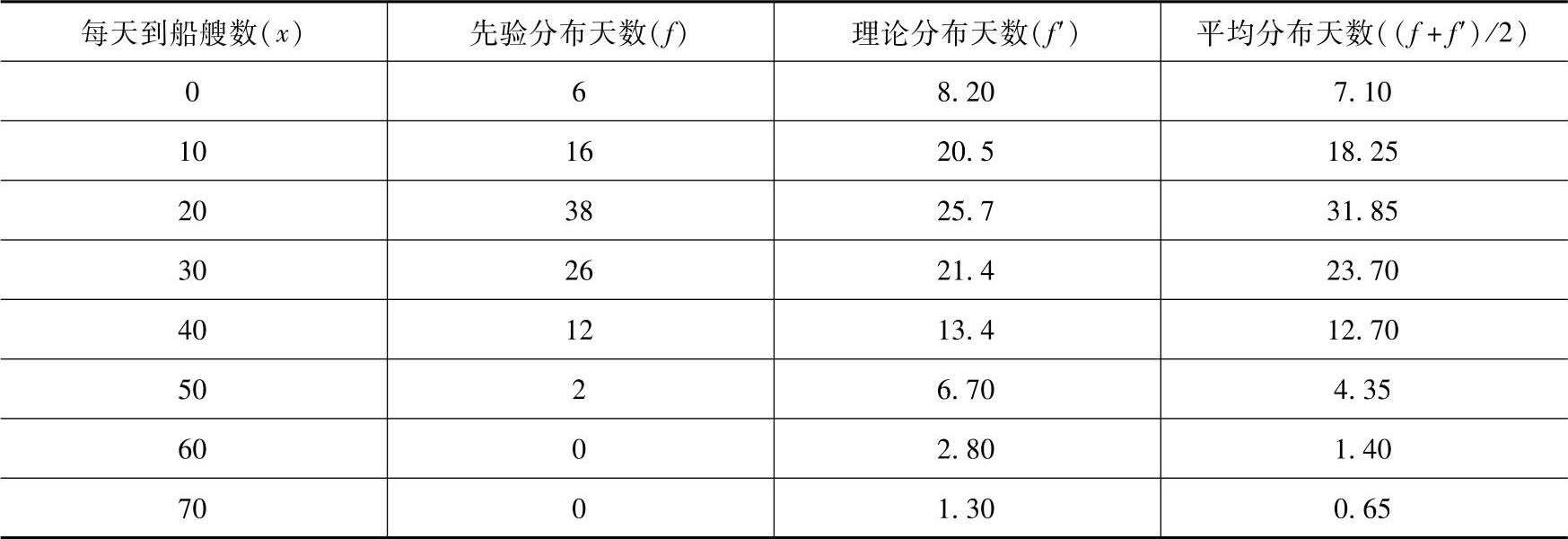
3）按照平均次数分布，求该港计划期预计到船总数，见表7-11。
表7-11 预计到船总数
4）求计划期每天平均到港船舶艘数：
2385.5/100=23.855≈23.9（艘）
即计划期每天平均到港船舶艘数约等于23.9艘，与约定的计划增长数λ=23.94基本相符。
5）计算每天到港船舶频率：有了每天船舶到港平均次数分布数以后，即可以按四舍五入将它们简化，并将每天到船为60艘及70艘的天数并入每天到船为50艘的天中，再将这个分布化为频率，见表7-12。
表7-12 每天到港船舶频率
6）求随机概率：将以上频率加以累计，并换算为随机概率，见表7-13。
第五步：利用随机概率进行模拟（略）。
表7-13 随机概率
[案例] 射击命中率问题
在我方某前沿防守地域，敌人以一个炮排（含两门火炮）为单位对我方进行干扰和破坏.为躲避我方打击，敌方对其阵地进行了伪装并经常变换射击地点。经过长期观察发现，我方指挥所对敌方目标的指示有50%是准确的，而我方火力单位，在指示正确时，有1/3的射击效果能毁伤敌人一门火炮，有1/6的射击效果能全部消灭敌人。现在希望能用某种方式把我方将要对敌人实施的20次打击结果显现出来，并确定有效射击的比率及毁伤敌方火炮的平均值。
解：
这是一个概率问题，只涉及简单的随机数的产生和处理，可以通过理论计算得到相应的概率和期望值。但这样只能给出作战行动的最终静态结果，而显示不出作战行动的动态过程。为了能显示我方20次射击的过程，考虑采用计算机模拟。
1.问题分析
需要模拟出以下两件事情：
1）观察所对目标的指示正确与否。模拟试验有两种结果，每一种结果出现的概率都是1/2。因此，可用投掷一枚硬币的方式予以确定，当硬币出现正面时为指示正确，反之为不正确。
2）当指示正确时，我方火力的射击结果。模拟试验有三种结果：
①毁伤一门火炮的可能性为1/3（即2/6）。
②毁伤两门火炮的可能性为1/6。
③没能毁伤敌火炮的可能性为1/2（即3/6）。
这时可用投掷骰子的方法来确定：
出现1、2、3点：则认为没击中敌人。
出现4、5点：则认为击毁敌人一门火炮。
出现6点：则认为击毁敌人两门火炮。
2.符号假设
i——要模拟的打击次数。
k1——没击中敌人火炮的射击总数。
k2——击中敌人一门火炮的射击总数。
k3——击中敌人两门火炮的射击总数。
E——有效射击比率。
E1——20次射击平均每次毁伤敌人的火炮数。
3.程序流程图
程序流程图见图7-10。
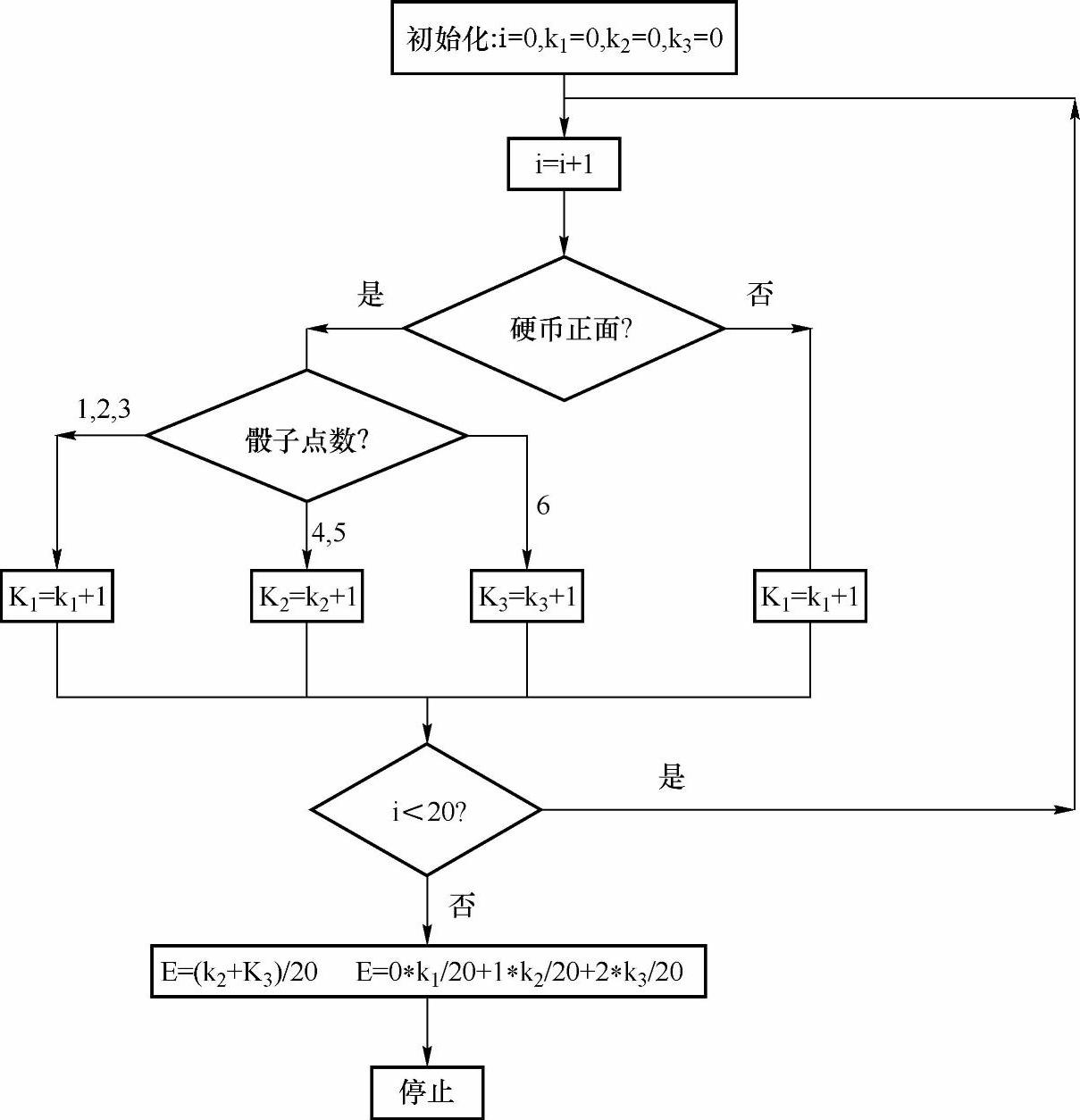
图7-10 程序流程图
4.模拟结果
模拟结果见表7-14。
表7-14 模拟结果
（续）
从表7-14的模拟结果可以计算出：
有效射击
E=7/20=0.35
平均值
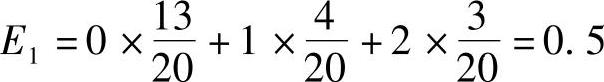
5.理论计算
设：
A0：射中敌方火炮的事件；A1：射中敌方一门火炮的事件；
A2：射中敌方两门火炮的事件。
则由全概率公式，可以得到：
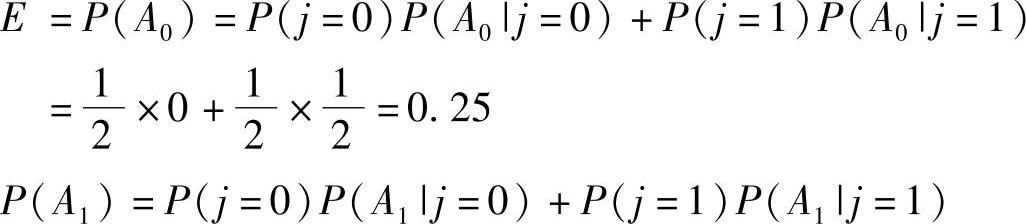
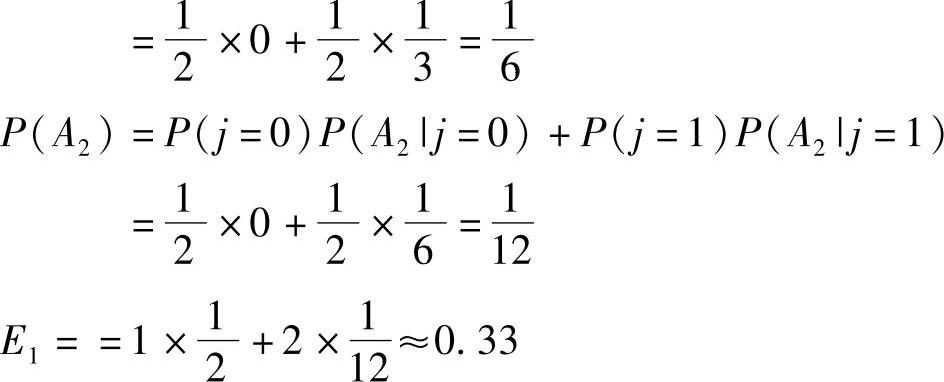
6.结果比较
理论计算和模拟结果的比较见表7-15。
表7-15 理论计算和模拟结果的比较
由表7-15可知，模拟结果与理论计算虽然结果不完全一致，但仍反映了事件发生的随机性。如果进行更多次实验求平均值，那么模拟值就会接近理论值。
有关系统工程学及应用的文章
定义变量在CADFEKO中左侧的树形浏览器中双击“Variables”结点，依次定义如下变量。圆波导半径：wg_r=0.51*lam。圆波导高度：wg_L=2*lam_w。按〈F5〉键，在3D视图中适中显示模型。图5-79 定义圆波导天线波导部分1在“Construct”菜单中单击“Cone”按钮，弹出“Create cone”对话框，如图5-80所示。在“Label”文本框中输入“Port1”，单击“Create”按钮。图5-85 定义端口激励WaveguideSource1重复上述步骤，在“Add waveguide source”对话框中进行如下设置。单击“3D pattern”按钮，修改theta的“Increment”为2，Phi的“Increment”为5.0。......
2023-10-31
PSCAD是当前主流的电力系统暂态分析软件，主要用于一般的交流电力系统电磁暂态研究，进行简单和复杂电力系统的故障建模及故障仿真，分析电力系统的故障电磁暂态过程。EMTDC/PSCAD还可以广泛地应用于高压直流输电、FACTS控制器的设计、电力系统谐波分析及其电力电子仿真。此外，EMTDC/PSCAD还具有强大的自定义功能，用户可以根据自己的需要创建具有特定功能的装置。......
2023-06-23
Unity引擎的更新迭代速度很快，从2017年开始每个季度都会有次大版本的更新，比如2017.1，2017.2等，至今正式的大版本升级到了2018.2版本。Unity LTS版本将从TECH版本每年最后一个版本开始，持续支持二年的时间。如果读者实际准备发布上线的项目，为了稳定起见，建议使用LTS版本，即2017.4最新的版本，以保证项目最大限度地稳定运行。如果发现没有红色报错信息，基本可以确定大部分版本升级是成功的。......
2023-10-17
天线单元的复制和激励的添加均在EDITFEKO中完成，下面介绍具体步骤。启动CADFEKO，新建一个工程“dipole_array.cfx”。由于阵列的单元尺寸是相同的，因此可以在EDITFEKO中通过循环来快速生成阵列，并完成对端口激励信号的快速定义。对话框，如图5-260所示，单击“Yes”按钮即可进入EDITFEKO界面。图5-260 选择是否锁定CADFEKO的求解设置每一个工程文件都会对应一个脚本文件，......
2023-10-31
在STEP7中启动PLCSIM进入仿真模式。2）启动后显示CPU仿真界面S7-PLCSIM1，如图6-62所示。下载项目前先选择正确的PG/PC接口，本例程仿真基于TCP/IP的S7通信，所以选择PLCSIM，如图6-63所示。在下载2#站点到PLCSIM前，需要再打开一个新的PLCSIM2进程如图6-65所示。图6-65 新建“PLCSIM”图6-66 PLCSIM2界面6）通信调试。将两个下载到PLCSIM中的站点CPU切换到RUN-P模式，打开Netpro查看激活的连接状态，可以看到连接已经建立成功，如图6-67所示。......
2023-06-18
6）按照表11-6所示将各个ET 200S模块从硬件目录拖动到组态表中，最后如图11-37所示。图11-38 数据包地址4.编程如图11-39所示进行ET200S的I/O测试，同时可以打开PLCSIM仿真程序进行验证，结果如图11-40所示。图11-39 I/O测试程序图11-40 PLCSIM仿真结果而在实际应用中，在PROFIBUS DP中进行启动ET200S的示意如图11-41所示。图11-41 PROFIBUS DP中进行启动ET200S......
2023-06-18
北京化工大学开发的12mm手提式高速排气挤出机、28mm熔体齿轮泵挤出机和CPJ75/135串联式磨盘挤出机都是特殊机的新成果。用于混炼工艺的特殊挤出机是未来的发展方向，如串联磨盘式螺杆挤出机、往复式销钉螺杆挤出机。图1-13b是串联式磨盘螺杆挤出机构成示意图，整体由挤出系统、润滑冷却和抽真空系统、加料系统、传动系统、电动机等组成。图1-13c则是串联式磨盘螺杆挤出机挤出系统结构图。......
2023-06-15
本节将介绍如何利用FEKO的CMA技术进行MIMO天线的快速设计。图10-74 MIMO天线结构启动CADFEKO，新建一个工程“MIMO_ring.cfx”。定义变量在CADFEKO中左侧的树形浏览器中，展开“Definitions”结点，双击“Variables”结点，依次定义如下变量。单击“Create”，如图10-75所示。把新生成的模型更名为“sector_2”。设置求解参数（特征模）在左侧的树形浏览器中，在“Configuration”选项卡中，在“Configur......
2023-10-31
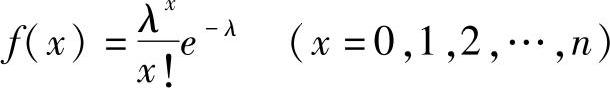
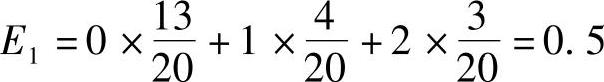
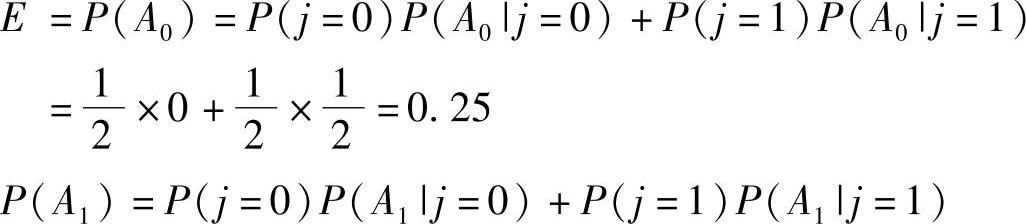
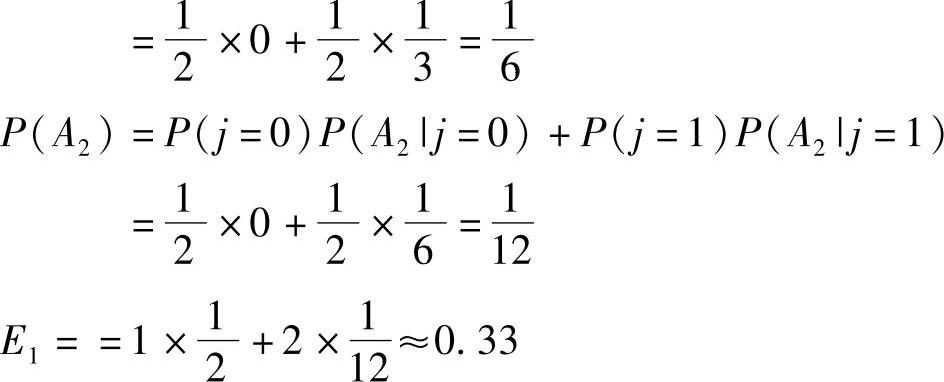
相关推荐