仿真数据的产生与分析详解

2023-07-15 理论教育版权反馈

【摘要】：离散事件系统仿真的基础就是产生随机数据。2）伪随机数的产生。3）产生泊松分布随机数据的技术如果相继两个事件出现的间隔时间服从于指数分布，则在单位时间内，事件出现的次数服从于泊松分布。

对随机现象进行模拟，实质上是要给出随机变量的模拟，即利用计算机随机地产生一系列数值，它们的出现服从一定的概率分布，称为随机数据。离散事件系统仿真的基础就是产生随机数据。

1.随机函数及随机数字的产生

确定随机变量的类型和选择合适的随机数产生方法。

（1）随机数指在区间（0，1）之间的随机采样值。

1）标准均匀分布随机数的性质。其密度函数表达式为

由均匀性和独立性的要求可以得到以下结论：

①对于子区间（L₁，L₂）0≤L₁<L₂≤1，观察值落在该区间的概率为L₂-L₁。

②一个观察值出现在一个特定的区间的概率与前面取出的数值无关。

2）伪随机数的产生。采用一个不变的公式来产生“随机”数，不具有真正的随机性，因此称其为伪随机数。虽然是伪随机数，但它们已能够有效地模仿均匀分布性和独立性的思想特性，从而可以满足系统仿真的需要。

线性同余法（Lehmer，1951）是一种伪随机数产生方法，可以根据如下递归关系式产生

式中，[]表示取整，显然有：0≤X_i≤m-1可以产生0到m-1之间的整数序列X₁，X₂，L。

令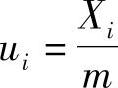，即可在之间取值，则当m充分大时，u_i将在（0，1）区间内取值。

（2）随机变量的产生方法进行仿真研究必须按照分布特性产生随机变量，其方法是在随机数字产生的基础上进行数字处理。

1）逆变换法产生随机数据。逆变换法可用来从指数分布、韦伯分布、均匀分布和经验分布中取得采样值。

①指数分布。指数分布的概率密度函数

累积分布函数

式中，参数λ可以解释为单位时间内事件发生的平均数。例如，如果到达时间间隔X1，X2，X3，…是具有λ的指数分布，那么λ可解释为单位时间内到达的平均数，或到达速率。

对任意i有E（X_i）=1/λ，1/λ是平均间隔时间。这里的目的就是给出一种产生具有指数分布的随机变量X的方法。指数分布的累积分布函数F（X）形式较为简单，可以比较容易的导出其逆F^-1，这样就可以采用逆变换技术。

逆变换步骤：

步骤1：计算需要产生随机变量X的累积分布函数。

步骤2：在X取值范围内，置F（X）=R。对于指数分布，在X≥0范围内，存在

1-e^-λX=R

由于X是随机变量，因此1-e^-λX也是一个随机变量。R是在区间（0，1）上均匀分布的随机变量。

步骤3：解方程F（X）=R

X=（-1/λ）ln（1-R）

步骤4：产生均匀分布随机数R₁，R₂，…，并由下式计算所需的随机变量

X_i=（-1/λ）ln（1-R_i）（7-23）

由于R_i和（1-R_i）都是区间（0，1）上的均匀分布的随机数，通常用R_i代替1-R_i，而得到简化的随机变量产生公式

X_i=（-1/λ）ln（R_i）（7-24）

②韦伯分布

其概率密度函数为

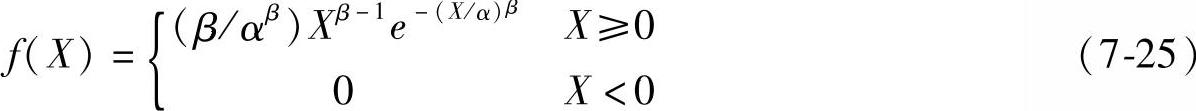
其中α>0，β>0分别是分布尺度和形状参数。

其累积分布函数为

由F（X）=R得随机变量

X=α[-ln（1-R）]/β

2）正态分布的直接变换产生随机数据。正态分布的累积分布函数

由于该函数无法求逆，故不可用逆变换法产生随机数。

直接变换法可以产生一对独立的均值为0、方差为1的标准正态分布的随机变量。计算公式为

Z₁=（-2lnR₁）/2cos（2πR₂）

（7-28）

Z₂=（-2lnR₁）/2sin（2πR₂）

对于均值为μ、方差为σ的正态分布随机变量可以利用变换Y=σ+μZ得到。

3）产生泊松分布随机数据的技术

如果相继两个事件出现的间隔时间服从于指数分布，则在单位时间内，事件出现的次数服从于泊松分布。泊松分布的概率函数为

f（n）=（λn/n！）e^-λn=0，1，2，… （7-29）

由于相继两个事件之间的间隔时间是一个服从于指数分布的随机变量，可以很容易地产生相应的随机数，如第i个间隔为yi=-1/λlnRi，其中Ri为（0，1）上的随机数，1/λ为指数分布的均值。

产生泊松分布随机变量N的具体步骤为：

步骤1：置n=0，S=1。

步骤2：产生一个随机数R_n+1，并用S*R_n+1代替S。

步骤3：若S<e-λ则接收N=n。否则，拒绝现在的n，并令n增加1，然后返回到步骤2。

要产生一个泊松分布随机变量N，若N=n，那么需要产生n+1个随机数。这样平均个数为（N+1）=λ+1，若泊松分布的均值λ较大时，则平均个数也较大。

4）查表法产生离散分布随机变量。设某一概率函数由下式给出

p（0）=p（X=0）=0.5；p（1）=p（X=1）=0.3；p（2）=p（X=2）=0.2

累积分布函数为

根据累积分布函数F（X）可构造表7-4，利用此表协助产生随机变量。

表7-4 累积分布函数表

产生一个（0，1）区间的随机数R_i，再找出R_i落入的区间：F（X_j-1）=r_j-1<R_i≤r_j=F（X_j），得到X_i=X_j。

2.输入数据分析

在离散事件系统仿真中，有些输入数据及模型参数是随机数，故需对输入数据进行分析，即确定各输入数据的分布及参数。输入数据的分析是项工作量很大的工作，同时也是直接影响仿真结果正确性的工作。其工作步骤有四项，分别为：

1）数据收集。

2）分布的识别。通过分析直方图、概率图可以对输入数据的分布做某种假设。

3）参数估计。样本均值和样本方差可用来估计所假设分布的参数。

4）分布假设检验。即对各输入数据假设的分布及估算得到的参数进行检验，看其假设的正确性。应用柯尔莫哥洛夫及斯米尔诺夫和卡尔拟合度检验。

3.输出数据分析

输出数据具有随机性，必须经过统计分析才能得到真实值。在进行仿真输出数据分析时，需要得到输出变量的点估计和区间估计。

点估计是取样本的一个函数作为未知参数的估计值，对于已给的置信概率，根据样本观测值来确定未知参数的置信区间，称为参数的区间估计。

（1）暂态仿真输出分析暂态仿真是指从指定的初始时刻0开始到某一时刻TE终止的一类仿真。E是停止仿真的一个指定事件，TE是结束仿真的特定时刻，它是由E事件发生来决定或者由人为预先指定。如仿真在9：00至21：00高峰期的交通情况等。

暂态仿真应尽量满足下列三个条件：

①初始条件设置正确，巨保证每次仿真运行在相同的初始条件下进行。

②随机数流的独立性。这是为了保证每次运行的随机性输入数据的独立性，从而使各次仿真运行也相互独立。

③假设输出结果服从正态分布，如不服从正态分布，则必须进行大量次数的运行，以遵从大数定律。大数定律是概率论中用来阐明大量随机现象平均结果稳定性的一系列定理。

（2）稳态仿真输出分析与主要方法

1）稳态仿真。它的研究对象是系统的稳态行为，如一个24h不间断的加工系统、城市的通信服务系统等。对这类系统应该仿真运行足够长的时间，理论上应是无限长的时间。当仿真时间不是无限长时，如何消除初始值影响以及如何在观测值下得到输出结果的点估计与区间估计，是稳态仿真输出分析的主要工作。

2）减少初始状态引起的偏差。为了减少此影响，可以将仿真运行分为两段：

第一段从零时刻到T0时刻，称为初始阶段；第二段是从T0到结束时刻TE。

在初始阶段，零时刻设置的初始条件对输出的影响较为明显，这时候不采集数据，而在T0到结束时刻TE时刻内采集数据，那时的数据就更能反映系统的稳态性能。

3）输出数据分析法。对离散事件系统的输出数据分析时，通常采用的两种方法或两种策略：

①固定样本量法：任意给定一个仿真运行长度，利用从有效过程中得到的有效数据来构造置信区间。

②序贯法：仿真运行长度序贯地增加，直到所构造的置信区间可以接受为止。决定仿真停止的技术通常有两种方法，即绝对精度停步规则和相对精度停步规则。

仿真数据的产生与分析详解

相关推荐