排队系统的结构与性能研究

2023-07-15 理论教育版权反馈

【摘要】：排队系统主要由提供服务者与被服务者组成，系统的主要功能就是服务。如图7-5所示是最简单的单服务台排队系统模型。有限顾客源模型中，到达率与进入系统等待或正接受服务的顾客数有着密切关系。服务机构不同，则排队系统的结构也不相同。目前，对排队系统进行仿真研究，主要目的就是要了解排队系统的性能。

排队系统主要由提供服务者与被服务者组成，系统的主要功能就是服务。同时，随机性是其固有属性，如被服务者的到达、服务时间的长短等。如图7-5所示是最简单的单服务台排队系统模型。

图7-5 单服务台排队系统模型

1.排队系统的描述

（1）顾客与顾客总体顾客指任何一种需要系统对其服务的实体，顾客总体是指潜在的顾客总数。它分为有限和无限两类，无限顾客源模型中，到达率（即每单位时间到达顾客的平均数）不受已经进入系统等待或正接受服务的顾客数的影响。有限顾客源模型中，到达率与进入系统等待或正接受服务的顾客数有着密切关系。

（2）到达模式到达模式是指顾客按照怎样的规律到达系统，它一般用顾客相继到达的间隔时间来描述。根据时间间隔的确定与否，到达模式可分为确定性到达和随机性到达。

随机性到达模式有：

1）泊松到达模式。需要满足四个条件：平稳性、独立性、普遍性和有限性。其到达分布函数

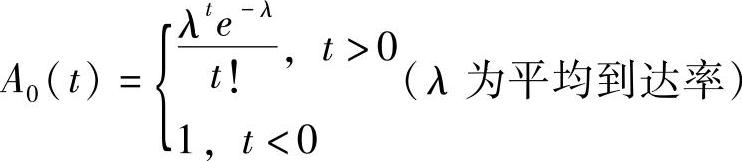
2）爱尔朗到达模式。这种到达模式常用于典型的电话系统，其到达分布函数为

λ为平均到达率，k为大于零的正整数。

3）一般独立到达模式，指到达间隔时间相互独立，分布函数A₀（t）是任意分布的到达模式。这种分布往往可以用一个离散的概率分布表加以描述。

此外还有超指数到达模式、成批到达模式。

（3）服务机构与服务时间

1）服务机构。是指同一时刻有多少服务台可以提供服务，服务台之间的布置及关系是什么样的。服务机构不同，则排队系统的结构也不相同。

2）服务时间。服务台为顾客服务的时间可以是确定的，也可以是随机的。

服务时间的随机分布有以下几种：

①定长分布：所有顾客被服务的时间均为某一常数。

②指数分布：当服务时间完全随机的时候，可以用指数分布来表示。

③爱尔朗分布：用来描述服务时间的标准差小于平均值的情况。

④超指数分布：与爱尔朗分布相对应，用来描述服务时间的标准差大于平均值的情况。

⑤一般服务分布：用于服务时间是相互独立但具有相同分布的随机变量的情况。

⑥正态分布：在服务时间近似于常数的情况下，多种随机因素的影响使得服务时间围绕此常数值上下波动，一般用正态分布来描述该服务时间。

⑦服务时间依赖于队长的情况。即排队顾客越多，服务速度越快，服务时间越短。

（4）排队规则是指顾客按什么样的次序与规则接受服务。

常见的排队规则有以下几类：

1）损失制。若顾客来到时，系统所有的服务机构均非空，则顾客自动离开，不再回来。

2）等待制。若顾客来到时，系统所有的服务机构均非空，则顾客就形成队列等待服务，具体包括：

①先进先出，即先到先服务。

②后进先出，后到先服务。

③随机服务：服务台得空时，从队列中任选一个顾客进行服务，这时候队列中每一个顾客被选中的概率相等。

④按优先级服务：一是当服务台得空时，队列中优先级最高的顾客先接受服务；二是当有一个优先级高于当前服务顾客的顾客来到时，按这样的原则处理。

⑤最短处理时间先服务。服务台得空时，首先选择需要最短服务时间的顾客来进行服务。

目前国内银行大多采用①、④规则并存的制度进行服务。

3）混合制。是损失制与等待制的综合类型。具体包括：

①限制队长的排队规则。

②限制等待时间的排队规则。

③限制逗留时间（包括等待时间和服务时间）的排队规则。

2.排队系统的符号表示

排队系统的符号表示的简要格式为：A/S/C/N/K。

其中：A：到达间隔时间概率分布（即到达模式）。

S：服务时间概率分布。A与S的具体形式有：M——指数分布；D——常数或确定性分布；E_k——k阶爱尔朗分布；G——一般独立分布。

C：并行服务台个数。

N：系统变量。

K：顾客源（总体）规模。

3.排队系统的性能研究

合理地解决顾客等待时间与服务台空闲时间的矛盾，使得服务质量与设备利用率都达到较高的标准。由于排队系统本身的概率规律性，要用解析方法来处理一个复杂的排队系统是十分困难的，而仿真成为解决这一问题的很好的方法。目前，对排队系统进行仿真研究，主要目的就是要了解排队系统的性能。

排队系统常用的性能指标：

（1）服务台的利用率

式中，λ是平均到达速率；μ是平均服务速率。

（2）平均等待时间W_q和平均逗留时间W

式中，D_i是第i个顾客的等待时间；n是已接受服务的顾客数。

式中，W_i是第i个顾客的在系统中逗留的时间，它等于该顾客排队等待时间D_i和接受服务的时间之和。

（3）平均队长L_q和系统中平均顾客数L

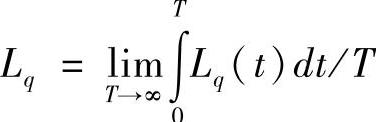
式中，L_q是t时刻的队列长度；T是系统运行时间。

其等价公式为

式中，q_i是时间区间[T_i，T_i-1]内排队人数。

式中，L（t）是t时刻系统中的顾客数；S（t）是t时刻系统中正在接受服务的顾客数。

（4）忙期（闲期）

忙期是指服务台全部处于非空闲状态的时间段；闲期是指服务台全部处于空闲状态的时间段。

4.排队系统仿真的建模

（1）仿真钟及推进离散事件系统一般不以时间推动，但事件之间有时序关系，仿真中仍必须有控制时间的部件。由于引起状态变化的事件发生时间的随机性，仿真钟的推进步长则完全是随机的，两个相邻发生的事件之间系统状态不会发生任何变化，因而仿真钟可以跨过这些“不活动”周期。仿真钟的推进呈现跳跃性，推进速度具有随机性。

离散事件系统仿真的仿真钟的推进方法有两种：

1）面向事件的仿真时钟，又称事件调度法。是按下一最早发生事件的发生时间来推进仿真时钟的方法。当采用这种方法时，每当某一事件发生，即将仿真钟推进到该事件发生时刻并立即计算其直接后续事件的发生时间，在处理完当前事件所引起的系统变化之后，从未来将发生的各类事件中挑选最早发生的任何一类事件，将仿真钟推进到该事件发生时刻，再作以上重复。这个过程中，仿真以不等距的时间间隔向前推进，直到仿真运行满足某终止条件为止。

2）面向时间间隔的仿真时钟，也称固定增量推进法。首先要确定某一时间单位T作为仿真钟推进的固定时间增量，即仿真钟从开始即按一时间单位T等距推进（跳跃），每次推进都需要扫描所有的活动，检查该时间区间内是否有事件发生。若无，则仿真钟继续等距推进；若有，则记录此时间区间，从而得到有关事件的时间参考数。若有若干事件同时发生，除了记录该事件的时间参考数外，还需事先规定这种情况下对各类事件处理的优先序列。

这种方法的缺点是时间增量T的确定较难，若T过大，则引入误差较大；若T过小，则由于每步都要检查是否有事件发生，增加了执行时间。除了具有较强的事件发生时间周期性的系统外，大部分离散事件系统的仿真采用面向事件的仿真钟推进方法。

（2）三种仿真建模方法建立仿真模型，也就是采用何种方法推进仿真钟，建立起系统中各类实体之间的逻辑联系。一般有三种方法，它们是：事件调度法、活动扫描法和进程交互法。

1）事件调度法。事件调度法是一种预定事件发生时间的方法。用事件的观点来分析真实系统，通过定义事件及每个事件发生时系统状态的变化，按时间顺序确定并执行每个事件发生时有关的逻辑关系。用这种方法建立仿真模型时，所有事件连同其发生均放在事件表中。模型中有一个时间控制模块，不断地从事件表中选择具有最早发生时间的事件，推进时钟到该事件发生时间，并调用与该事件类型相应的事件处理模块，处理完后再回时间控制模块。如此重复执行，直到满足仿真终止条件为止。

2）活动扫描法。基本思想：系统中的实体包含活动，这些活动的发生必须满足某些条件（活动的发生时间也是条件之一），同时每一个能主动产生活动的实体均有相应的活动子例程。具体实现措施：

①除系统仿真钟外，还设置了实体仿真钟。系统仿真钟表示系统仿真进程的推进时间，而实体仿真钟记录该实体的活动发生时刻。

②设置条件处理模块。此模块用来测定活动发生的条件是否满足。

这条措施的关键是建立活动子例程，包括此活动发生引起的实体自身状态变化以及对其他实体产生的影响等，然后用条件处理模块来控制仿真的推进，即对满足条件的活动调用其相应的活动子例程进行处理，处理完后再返回条件处理模块。如此重复执行直到仿真活动的终止。

3）进程交互法。采用进程来描述系统，它将模型中能主动产生活动的实体历经系统时所发生的事件与活动按时间顺序进行组合，形成进程表。一个实体一旦进入进程，它将完成该进程全部的有关活动。

以上三种仿真建模方法各有优缺点，其中：

事件调度法建模灵活，可应用范围相对较广。活动扫描法对于各事件之间相关性很强的系统来说，模型执行效率高，但需要用户对各实体的活动建模，仿真执行程序也较复杂。进程交互法的建模最为直观，其模型表示接近实际系统，特别适用于活动可以预测、顺序比较确定的系统，但是其流程控制复杂，建模灵活性较差。

（3）仿真流程图如图7-6所示是事件调度法仿真流程图。

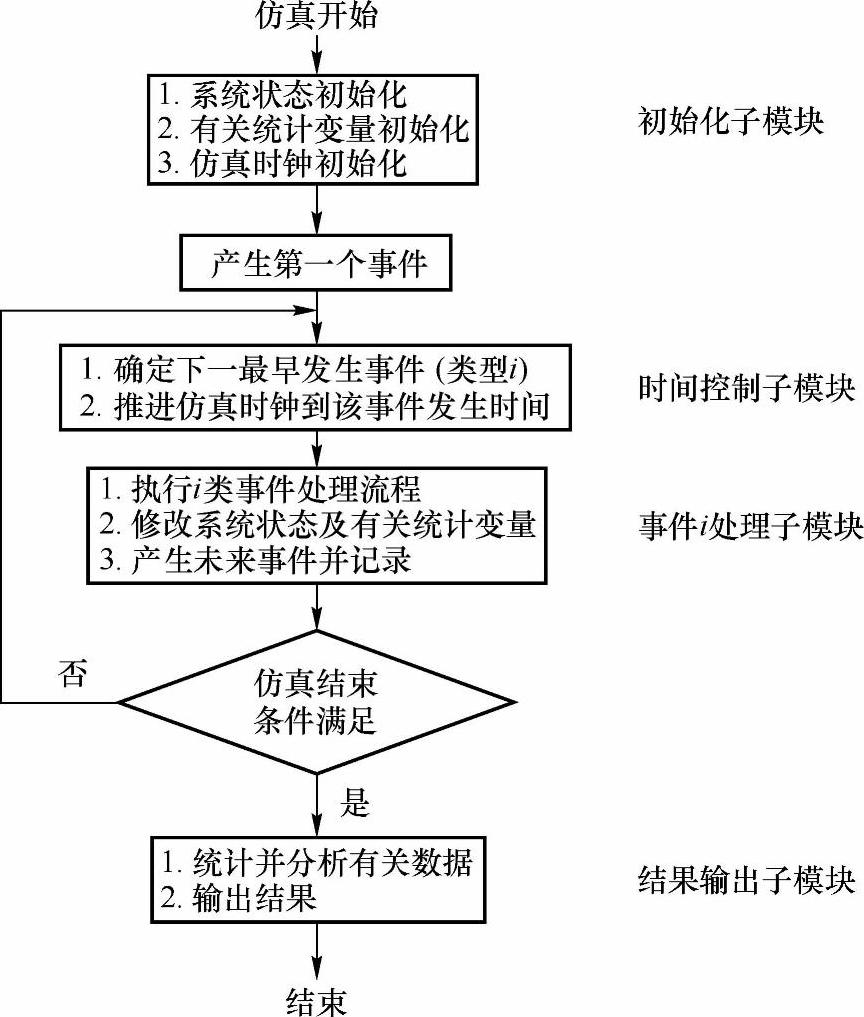
图7-6 事件调度法仿真流程图

5.单服务台排队系统仿真

此时，顾客到达模式与服务时间的分布可为任意一种分布类型。假定第i个顾客服务结束离去时刻正是第（i+1）个顾客服务开始时刻。这样一来，所有事件可归为两类，一是顾客到达事件，二是服务结束离去事件。当离去事件与到达事件同时发生时，先处理前者，再处理后者。

以单人理发店（M/M/1）为例。令仿真终止时间TT=240min，λ=μ=0.1。定义到达时间为1类事件，顾客离去事件为2类事件。排队规则为FIFO。其仿真过程及结果见表7-1。

表7-1 单服务台排队系统仿真表

6.多服务台排队系统仿真

多级多服务台排队系统的示意图如图7-7所示。多服务台排队系统仿真见表7-2。

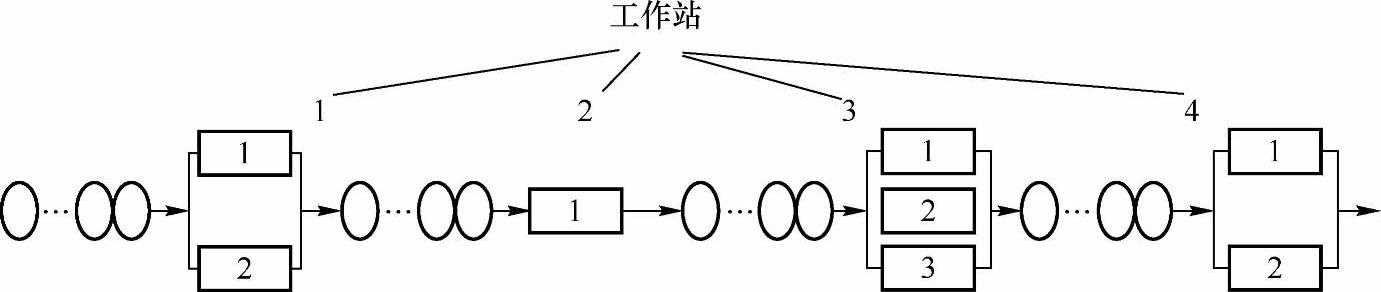
图7-7 多级多服务台的排队系统

此时，顾客到达模式与某工作站顾客接受服务的时间各服从一定的分布。处理规则：若顾客到达时间与顾客离开时间相同，则先处理离开事件，再处理达到事件。若不同顾客离开不同工作站时间相同，则按工作站编号由小到大处理离开事件。若工作站内顾客离开不同服务台时间相同，按服务台编号由小到大处理离开事件。仿真时一般采用事件调度法建立仿真模型（仿真过程略）。

该类系统研究的一个十分重要的问题就是寻找所谓“瓶颈”点。由于系统中服务台的负荷不均造成的阻塞或拥挤现象，具体反映为某个工作站或服务台的平均队长太长，或平均利用率远远高于其他工作站或服务台，这对整个系统的效率是不利的。这时需要仿真结果输出：各工作台（或服务台）的平均队长、平均利用率、顾客平均等待时间等，来了解系统仿真性能。

表7-2 多服务台排队系统仿真

排队系统的结构与性能研究

相关推荐