马尔柯夫模型预测法的介绍

2023-07-15 理论教育版权反馈

【摘要】：具备这个性质的离散型随机过程，称为马尔柯夫链。，T）经常使用马尔柯夫预测法对商品市场占有率进行预测，其一般步骤为：1）调查目前的市场占有率情况。

1.概念

马尔柯夫模型预测法是以俄国数学家A.A.Markov名字命名，是应用概率论中马尔柯夫链的理论和方法来研究随机事件变化并借此分析预测未来变化趋势的一种方法。它是利用状态之间转移概率矩阵预测事件发生的状态及其发展变化趋势，也是一种随机时间序列分析法。

在20世纪初，马尔柯夫在研究中发现自然界中有一类事物的变化过程仅与事物的近期状况有关，而与事物的过去状态无关。例：设备维修和更新、人才结构变化、资金流向、市场需求变化等许多工程、经济、社会行为都可用这一类过程来描述或近似。

具体来说，马尔柯夫链就是一种随机时间序列，它在将来取什么值只与它现在的取值有关，而与它过去取什么值无关，即无后效性。具备这个性质的离散型随机过程，称为马尔柯夫链。

2.预测模型

把事件发生各结果的概率记为一向量的元素，则可写成

S（t）=[S₁（t），S₂（t），…，S_n（t）]

并存在

当能够知道从t时期到t+1时期的过程中，从每一结果i（i=1，2，…，n）向结果j（j=1，2，…，n）转变的概率P_ij时，则可得到如下转移矩阵

且

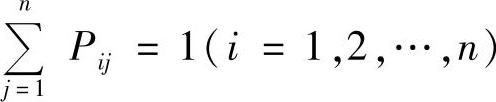
利用P矩阵后乘状态向量S（t），就可得到t+1时期概率分布状态向量S（t+1），即

S（t+1）=（S₁（t+1），S_S（t+1），…，S_n（t+1））=S（t）P （6-59）

具体地说，在第t+1时期，结果j出现的概率为

其他时期的概率分布状态向量为

S（t+2）=S（t+1）×P=S（t）×P×P=S（t）P² （6-61）

……

S（t+k）=S（t）P^k

（k=1，2，…，T）

经常使用马尔柯夫预测法对商品市场占有率进行预测，其一般步骤为：

1）调查目前的市场占有率情况。

2）调查消费者的变动情况。

3）建立数学模型。

4）预测未来市场的占有率。

[案例] 设某地区有甲、乙、丙三家企业，生产同一种产品，共同供应1000家用户。假定在10月末经过市场调查得知，甲、乙、丙三家企业拥有的用户分别是：250，300，450户，而11月份用户可能的流动情况见表6-12。要求：根据这些市场调查资料预测11、12两个月，三家企业市场用户各自的拥有量。

解：

表6-12 11月份用户可能的流动情况

根据调查资料，确定初始状态概率向量为

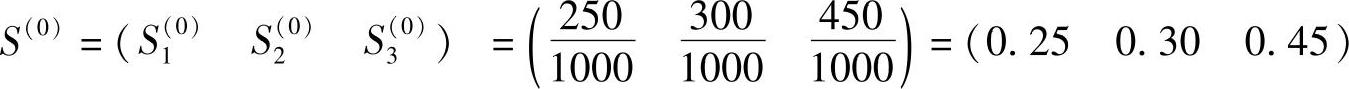
根据市场调查情况，确定一次转移概率矩阵为

利用马尔柯夫预测模型迸行预测，11月份三个企业的市场占用率为

所以在11月份这三个企业的市场占用率分别为：甲企业280户，乙企业270户，丙企业450户。可见丙的用户属于最多。

如果12月份用户可能的流动情况与11月份相同，则转移概率矩阵仍然为

12月份三个企业的市场占用率为

所以在12月份这三个企业的市场占用率分别为：甲企业306户，乙企业246户，丙企业448户，很显然，丙企业的市场占用率继续维持第一。