情景分析预测法就是在长期预测时，能够辨识关键因素及其影响方法。情景分析预测法具体有未来分析法、目标展开法和间隙分析法。图6-7 情景预测法的工作步骤[案例] 用情景预测分析法预测我国GDP发展趋势1.确定主题预测国内生产总值发展趋势。因为2006年与2005年相比，增长速度为23.9%，故以此作为情景A，对此迸行运算，可得2007年国内生产总值的预测值。......
2023-07-15
回归模型预测法：优化方法探究
【摘要】：回归模型分析预测法是根据事物内部因素变化因果关系来预测事物未来发展趋势。4）利用模型进行预测。图6-11 社会总产值预测值置信区域示意图6.3.3.2 多元线性回归预测法当预测对象Y受到多个因素X1、X2、…、Xm的影响，如果各个因素Xi与Y相关关系可以同时近似用函数关系来表示，则可以用多元线性回归预测模型进行预测。
回归模型分析预测法是根据事物内部因素变化因果关系来预测事物未来发展趋势。回归，regression，源于生物学界。在19世纪，英国生物学家高尔顿在研究人体遗传特征时发现的现象。他把人体身材趋于人平均高度现象称为“回归”；再加上后人提出的“相关”概念，就形成了独特的理论和方法体系——回归分析。
回归分析是一种数理统计方法，它是建立在大量数据基础上寻求数据变化的一种方法，也称“因果法”。事物变化的因果关系可用一组变量描述，即自变量与因变量之间的关系。其依存关系分二类：一是确定性关系——变量关系可用函数关系表达，如V（总产值）=P（单价）×（数量）；二是非确定性关系——变量间的关系只能通过观测大致地或平均地说明量与量之间的统计关系。如：商品的价格与销售量之间的关系，虽具不确定性，但仍然存在着某种统计性质的关系。回归分析就是通过对观测值的统计分析，确定它们之间联系形式的一种有效方法。比如以下几种关系可以采用回归分析建立数学模型：
①人的年龄与身高。
②人口的增长与道路建设的总里程。
③居民收入与银行存款。
④车辆拥有量与交通事故。
⑤车辆拥有量与维修量。
⑥道路里程与交通事故。
回归分析按变量个数，可分为一元回归分析和多元回归分析。如果按照变量间关系，则可以分为线性和非线性回归分析。
1.回归分析预测原理
通过分析，建立变量间确定函数关系；或通过数理统计方法建立起变量间回归方程，从而对变量间密切程度进行描述，并实现对变量回归估计和预测。
2.回归分析预测步骤
1）进行相关分析。若没有相关关系，则不能利用回归预测模型进行预测；若存在相关关系，则进一步确定变量间是线性关系还是非线性关系，然后进行下一步工作。
2）计算回归模型中的系数。
3）建立回归预测模型，写出变量间回归方程式。
4）利用模型进行预测。
5）预测值置信度检验：预测值是否可信？其波动范围如何？需作置信度的检验。
以上预测步骤可用如图6-9所示的框图来表示。
3.回归分析适用范围
变量之间需要存在相关关系。
4.回归分析方法优劣
①优点：需要数据量少，巨当回归方程的置信度较高时，预测精度高。
②缺点：非线性回归模型求解略微困难。
6.3.3.1 一元线性回归分析模型
该模型用于分析一个自变量X与一个因变量Y之间线性关系的数学方程。一般形式的数学模型为
Y=a+bX （6-26）
其中：Y是因变量；X是自变量；a是常数；b是回归系数。
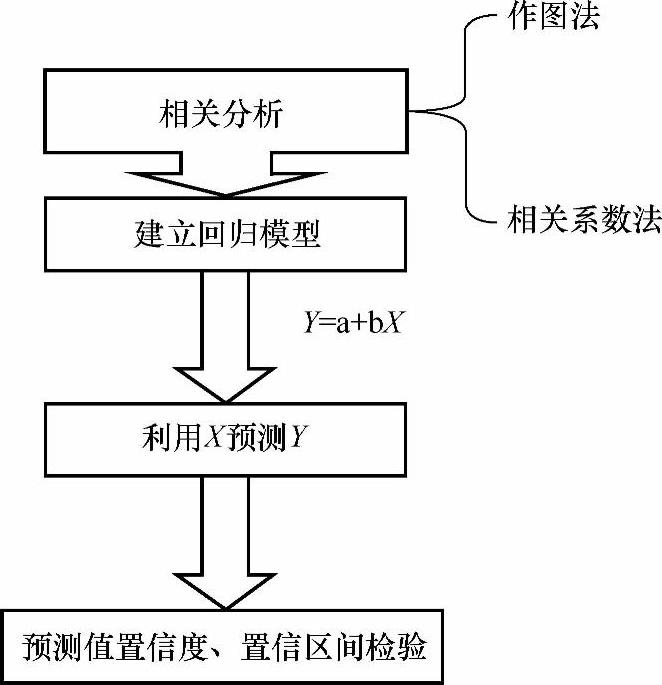
图6-9 回归分析预测步骤
模型的离差为
对应的离差平方和
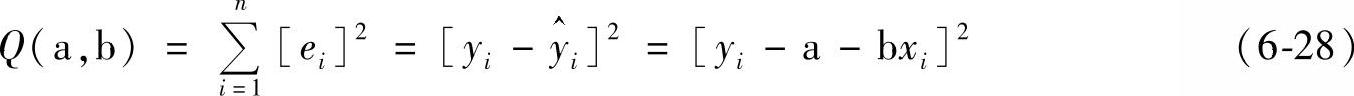
根据最小二乘法原理，离差平方和最小反映n个统计数据与回归方程总偏离程度最小，即
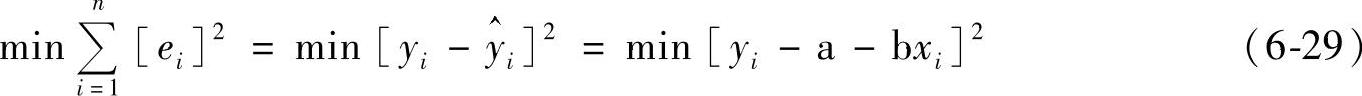
由微积分中极值原理，使方程（6-29）为最小的a和b存在，巨
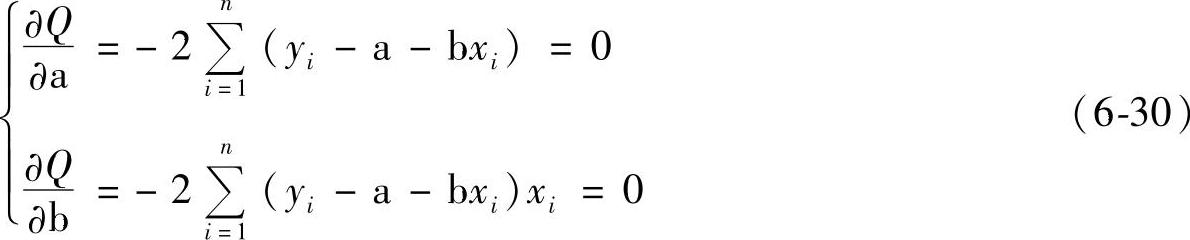
由方程（6-30）可求得
其中
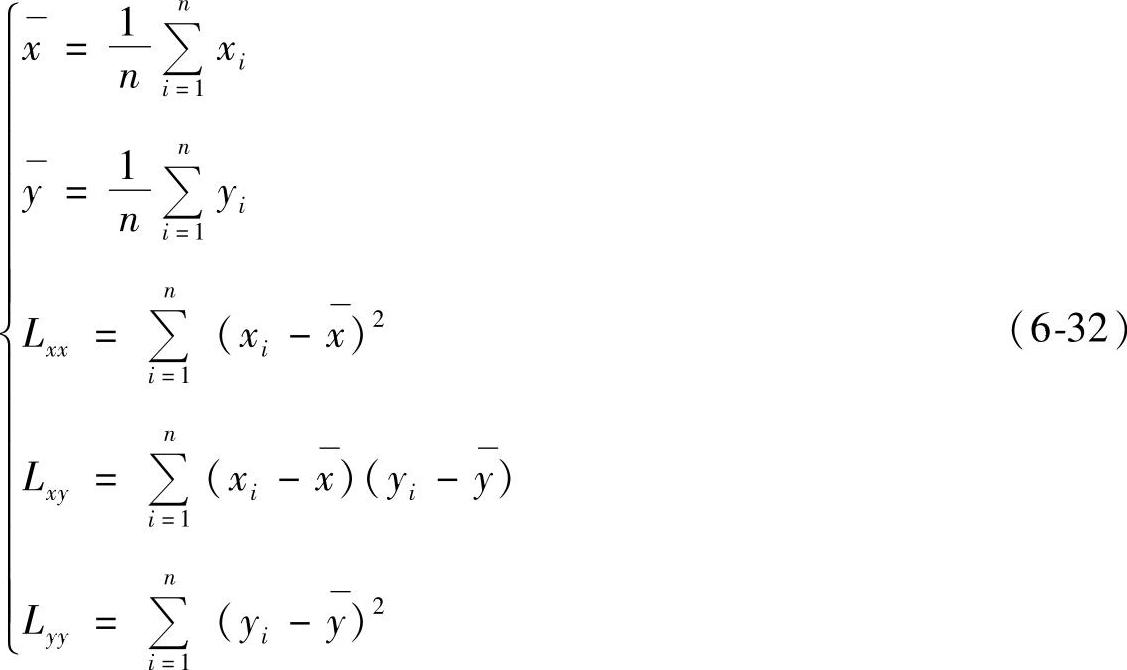
1.相关系数及相关系数检验
定义相关系数
相关系数是Y与X之间线性相关程度指数。相关系数检验所要解决的问题是：已知n个数据（xi，yi）之间是否确有线性回归关系存在？或者说，我们所采用的线性表达式在多大程度上是可信的。
一般地，r≤1。当r=1时，变量X与Y称为完全线性相关；当r=0时，变量X与Y称为完全不线性相关；当0<r<1时，Y与X之间存在着一定的线性相关关系；r越接近1，Y与X之间的线性相关程度越显著。
2.线性相关的显著性检验
设X与Y为两个正态母体，给定显著水平α，当r≥rα时，则表明样本拒绝假设H0，也就是说变量X与Y确实线性相关，得到的回归直线是合理的。rα为临界值，与样本容量n及显著水平α有关，具体数值可查表6-9。一般的，α为5%或者1%。
表6-9 γα的临界值
注：α为显著水平，反映y与x相关系数的置信水平为100（1-α）%；n-2称自由度，等于观测值个数减去回归方
程的变量数.
3.确定置信区间
当回归模型确有意义时，对于由回归模型求得的预测值y允许在多大范围或区间内变动，一般要求实际值位于这个区间范围内的概率应达到95%以上。这个区间被称为预测值的置信区间，它说明回归模型的适用范围或精确程度。
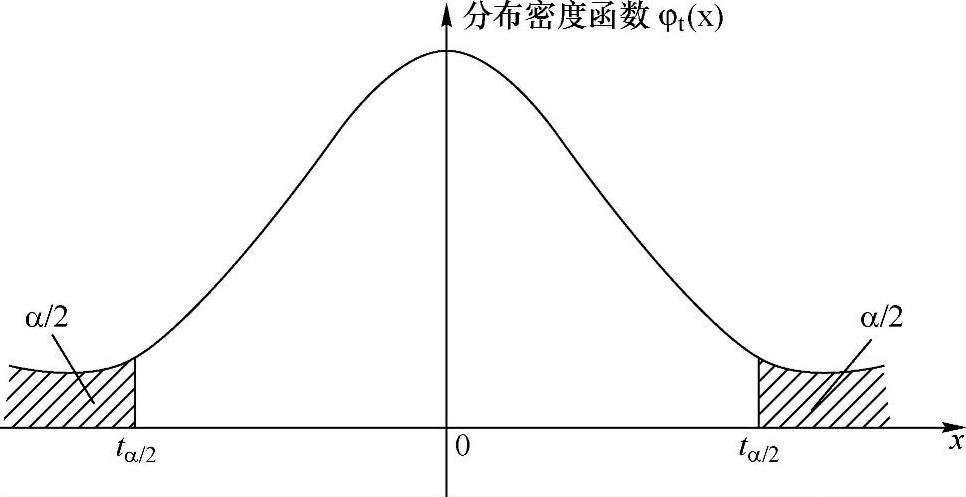
图6-10 置信区间
当观测值个数（或样本容量）n>30时，置信区间应为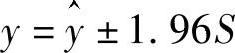
，其中S为标准离差，
即
当观测值个数（或样本容量）n≤30时，置信区间应为
其中S为标准离差，t（α/2，n-2）可通过查t分布表获得，α为显著水平，巨修正系数
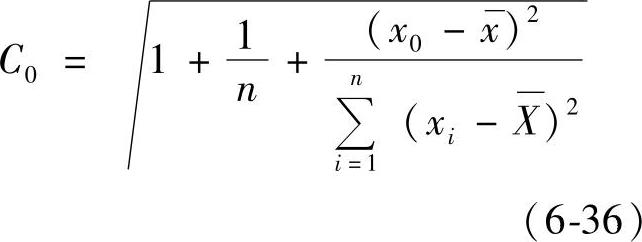
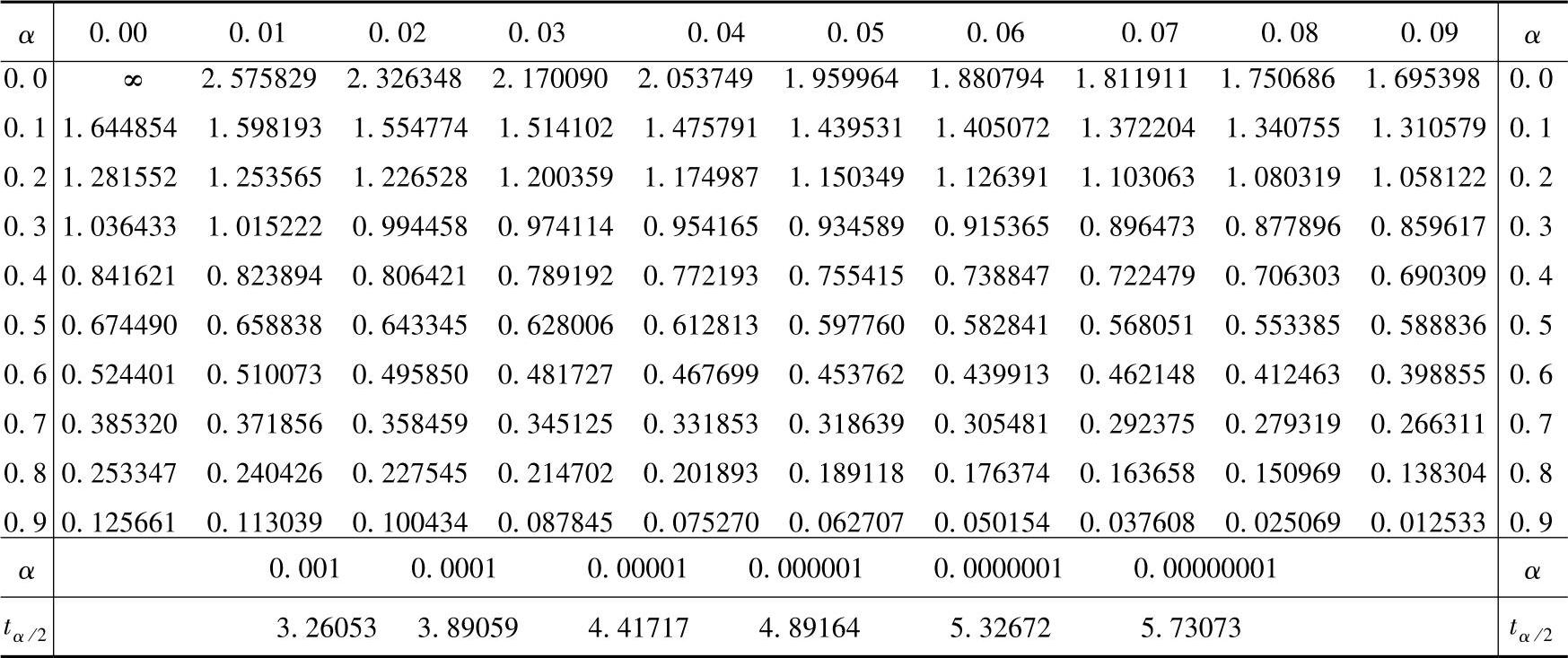
其中置信区间为如图6-10所示的非阴影部分。正态分布的双侧分位数（tα/2）见表6-10。
表6-10 正态分布的双侧分位数（tα/2）
[案例] 某市杜会总产值与货运量之间的关系见表6-11，预测当某市的货运量达到50千万吨时，该市的杜会总产值是多少？
表6-11 某市社会总产值与货运量之间的关系
解：
（1）相关分析
①作图法。
②相关分析计算
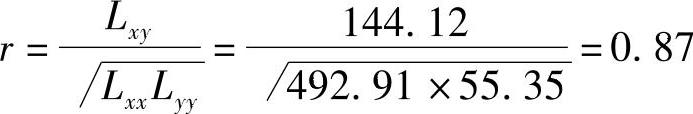
而查表6-9，r0.05=0.878，r≈ra。
所以杜会总产值与货运量之间存在确定的线性关系。
（2）计算模型中的参数
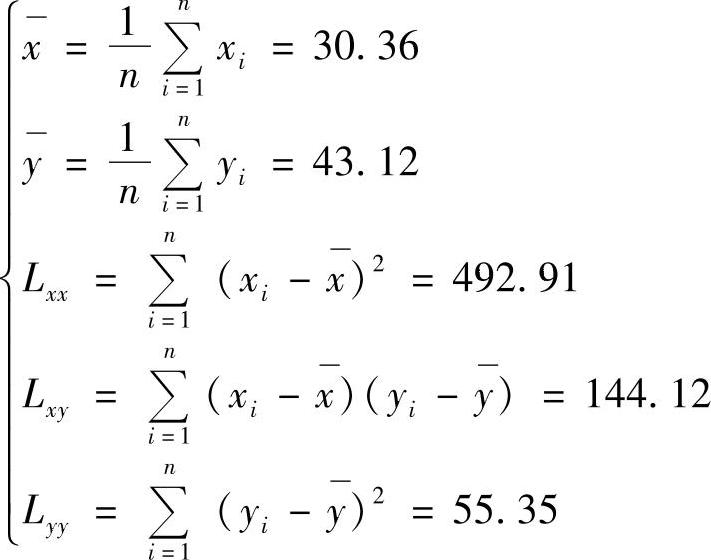
把以上数据代入公式（6.3.25）中，计算得到模型参数
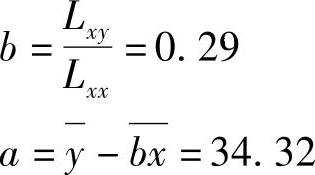
（3）建立回归预测模型
Y=34.32+0.29X
（4）利用模型迸行预测
Y=34.32+0.29×50=48.82（亿元）
（5）预测置信度检验
①剩余标准差
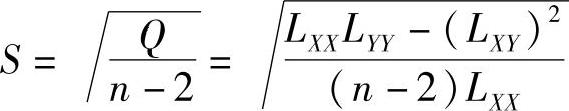
②在给定的置信度（1-α）（置信概率）或置信水平α（不可信概率）下，对于X的任一值X0，便可得到相应的Y0的置信区间：[Y0-tα/2S，Y0+tα/2S]，此时，设C0≈1。
③对于X0=50（千万吨），Y0=48.82亿元
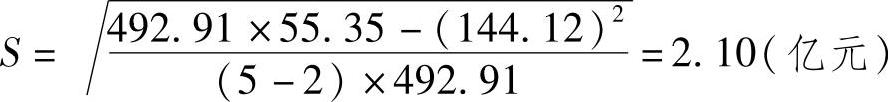
Y0的置信度为95%，α=0.05，查表6-10得：tα/2=2.26
Y0的置信区间：[48.82-2.26×2.10，48.82+2.26×2.10]=[48.82-4.746，48.82+4.746]=[44.074，53.566]
社会总产值预测值的置信区域如图6-11所示。
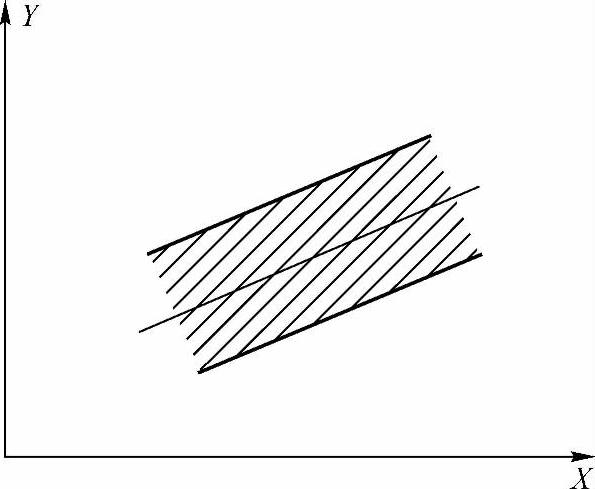
图6-11 社会总产值预测值置信区域示意图
6.3.3.2 多元线性回归预测法
当预测对象Y受到多个因素X1、X2、…、Xm的影响，如果各个因素Xi与Y相关关系可以同时近似用函数关系来表示，则可以用多元线性回归预测模型进行预测。其预测模型基本形式如下
Y=b0+b1X1+b2X2+…bmXm+σ （6-37）
式中，b0，b1，b2，…bm，σ是与X1，X2，…，Xm无关的常数。
设样本观测值为（Xk1，Xk2，…Xkm，Yk），k=1，2，...，n，记
Q=∑[Yk-（b0+b1X1+b2X2+…bmXm）]2 （6-38）
应用最小二乘法，分别对各参数求偏导数，可得到下列方程组
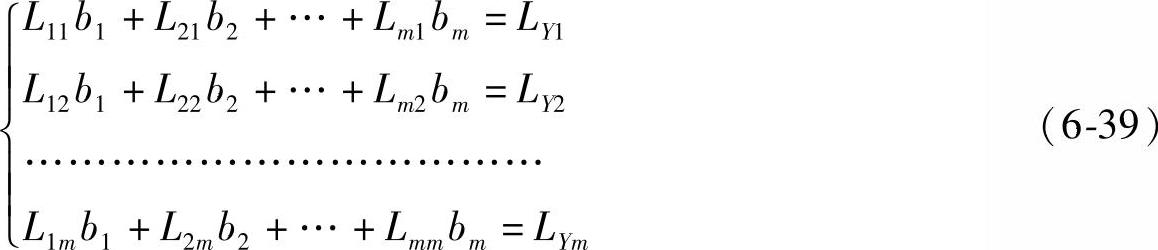
由上式求解得到b1，b2，b3，…，bm，把它们代入公式（6-26），即可得到：
多元线性回归的相关性检验和预测值置信度检验与一元线性回归的相关性检验和预测值置信度检验相似。如二元线性回归相关系数为
其中R称为Xi对于Y的全相关系数。
二元线性回归剩余标准差
对应的置信区间为
[Y0-tα/2S，Y0+tα/2S] （6-43）
公式中各参数符号的意义见前面的解释。
6.3.3.3 非线性回归分析
当因变量与自变量间关系不是直线关系，而是曲线关系时，需要采用非线性回归分析模型进行建模，并进行预测。
非线性回归按照自变量的个数，分为一元和多元非线性回归。非线性模型包括了双曲线、指数曲线和S型曲线等。此时，可以采用变量代换法把非线性回归问题转换成线性回归问题来处理。下面介绍几种常用的非线性回归模型。
（1）多项式曲线或抛物线形模型
Y=a+b1X+b2X2 （6-44）
设X=X1，X2=X2
则Y=a+b1X1+b2X2变成了一个二元线性回归方程。
（2）双曲线函数模型
1）
令y′=xy，则y′=a+bx
求解a和b后，再将a和b代入原方程，得到
2）
令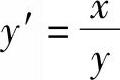
，则y′=a+bx
求解a和b后，再将a和b代入原方程，得到
（3）幂函数模型（y=axb）
lny=lna+blnx
设y′=lny，a′=lna，x′=lnx
y′=a′+bx′
求解a′和b，然后将a′还原为a，代入原方程，得
（4）指数函数模型
1）y=aebx
lny=lna+bx
设y′=lny，a′=lna
则y′=a′+bx
求解a′和b，然后将a′还原为a，代入原方程，得
2）y=aeb/x
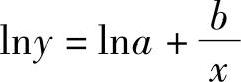
设y′=lny，a′=lna，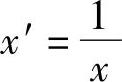
则y′=a′+bx′
求解a′和b，然后将a′还原为a，代入原方程，得
3）y=a-brx
令x′=-rx，则y=a+bx′
求解a和b后，再将a和b代入原方程，得到
（5）对数函数模型
y=a+blgx （6-53）
令x′=lgx，则y=a+bx′
求解a和b后，再将a和b代入原方程，得到
（6）逻辑斯蒂函数模型
令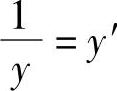
，x′=e-x则y′=a+bx′
求解a和b后，再将a和b代入原方程，得到
有关系统工程学及应用的文章
- 详细阅读
-
GM(1,1)预测模型的优化方法详细阅读
目前使用最广泛的灰色系统预测模型是一个变量、一阶微分的GM(1，1)模型。(一)GM(1，1)模型的一般形式定义1设序列X＝(x(0)(1)，x(0)(2)，…，x，x(n+1))建立的模型为新陈代谢GM(1，1)。(二)GM(1，1)模型检验GM(1，1)模型的检验包括残差检验、关联度检验和后验差检验。若相对残差、关联度、后验差检验在允许的范围内，则可以用所建的模型进行预测，否则应进行残差修正。......
2023-07-18
-
市场调查预测法的优化方法详细阅读
企业通过市场调查分析和预测产品的需求量、销售量、市场占有率及市场潜力等。市场调查预测法包括典型调查推算法、抽样调查推算法和全面市场调查法。也有学者把市场调查预测法划分为：用户需求意见调查预测法、业务人员意见调查预测法和经理人员意见调查预测法。......
2023-07-15
-
灰色模型预测法在6.3.5章节的优化详细阅读
灰色系统理论是研究解决灰色系统分析、建模、预测、决策和控制的理论。灰色系统理论认为对既含有已知信息又含有未知或非确定信息的系统进行预测，就是对在一定方位内变化的、与时间有关的灰色过程的预测。其用等时间距观测到的、反应预测对象特征的一系列数量值，构造灰色预测模型，预测未来某一时刻的特征量，或预测达到某一特征量的时间。......
2023-07-15
-
结构模型解析法及其优化方法详细阅读
结构模型解析法是美国Bottele研究所华费尔特教授于1973年在分析复杂社会经济系统问题时提出的。4）根据要素明细表作构思模型，并建立邻接矩阵和可达矩阵。5）对可达矩阵进行分解后建立结构分析模型。下一步利用上面获得的可达矩阵迸行系统结构的层次分析。......
2023-07-15
-
数学模型预测结果的优化详细阅读
计算结果从定性上与相应河段模型试验结果一致，定量上略有差别。小浪底水库调节后，出库沙量大幅度下降，特别是大于0.025m 的中、粗沙大部分被拦截在库区。......
2023-06-23
-
灰色数列预测方法优化详细阅读
根据数据序列建立GM(1，1)模型的步骤大致可以概括如下。这时所有模型的系数都相等，称相应的预测灰数为预测的唯一白化值。在应用时，只需要根据预测的超前长度来适当选择子序列的长度进行建模与预测。......
2023-06-30
-
系统动力学预测法及其优化详细阅读
系统动力学预测法具有以下特点1）善于解决高阶、非线性的复杂问题。用系统动力学预测法进行预测的主要步骤1）把被研究系统划分成若干子系统，并巨建立各子系统的因果关系、反馈耦合关系。系统动力学预测法在环境影响评价和对策分析、环境效益与经济效益综合研究中有重要价值。......
2023-07-15
相关推荐