移动平滑法就是对所取得的统计数据逐点推移,分段平均,以期最后得到一组具有较明显趋势的新数据。移动平滑法的预测程序框图见图9.2。图9.2移动平滑法的预测程序框图 某灌区历年人均林果产值见表9.3,试用移动平滑法建立预测模型,并求1999—2005年该灌区人均林果产值的预测值。图9.3人均林果产值的自然曲线及移动平滑预测曲线图由图9.3可知,对于直接用一次或二次移动平滑模型预测会出现滞后现象。......
2025-09-29
平滑预测法就是根据过去演变特征预测对象自身时间过程演变规律及未来趋势。它也属于时间序列预测法一种,不考虑随机性,短期预测较准。它起源于19世纪80年代,当时西方国家用它来进行经济周期波动研究和商情预测。
平滑是平滑预测法的核心,它是数据处理一种手段,可消除原始数据中的起伏波动,得到比较平滑的新数据,使预测对象演变特征和发展趋势明显呈现出来。在此基础上,再以平滑后新数据为变量,建立预测模型,进行预测。
平滑预测法包括了移动平均预测法和指数平滑法。其中移动平均预测法包括了一次移动平均法和二次移动平均法。指数平滑法包括一次指数平滑法、二次指数平滑法和三次指数平滑法。
1.移动平均预测法
移动平均预测法就是从原时间序列第一项开始,按一定项数N求算术平均数,并逐项推移,边移边平均,这样得到由移动平均数构成新时间序列数据,既把原序列中某些不规则波动平滑修匀,又不致使数据点数减少过多和形成分段台阶,从而使数据演变趋势较为明显的一种方法。
移动平均可以消除或减少时间序列数据受偶然性因素干扰而产生的随机变动影响。移动平均法在短期预测中较准确,而在长期预测中效果较差。
(1)第一次移动平均——简单移动平均法

式中,N是每段数据的个数。
上式可以简化为

公式中,选取N应遵循的原则:
①如果数据点多,则选取的N大;反之,则小。
②要考虑预测对新数据适应的灵敏度要求。若灵敏度要求高,则取N小;若平稳性要求高,则取N大。可试取几个N值,进行多方案比较。
其预测公式为
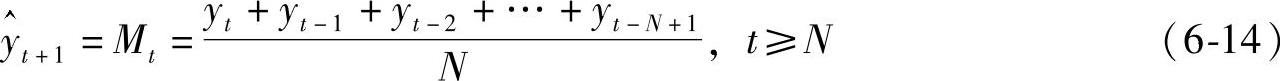
(2)第一次移动平均——加权移动平均法 是在简单移动平均法的基础上,根据最近几期观察值对预测值的影响大小给予不同的权数,而以加权后的平均值作为下一期预测值的预测方法。
其预测公式为
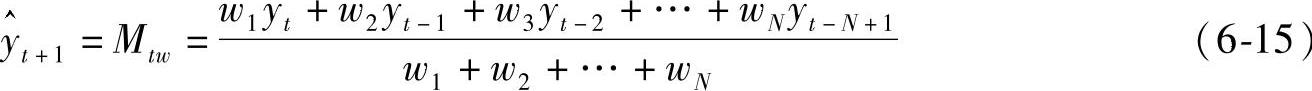
公式(6-15)就是加权移动平均预测法。在该式中,Mtω是第t期加权移动平均数;ωi是yt-i+1的权重数。
(3)第二次移动平均预测法 第二次移动平均是在第一次移动平均取得数据的基础上进行,目的使数据更为平滑一些,演变趋势更为明显。移动平均原理与第一次相同。
其数据计算公式为
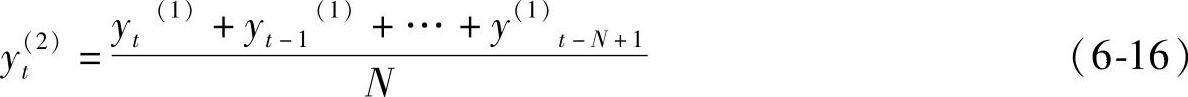
式中,N是每分段数据的个数。
第m次移动平均数据的计算公式为
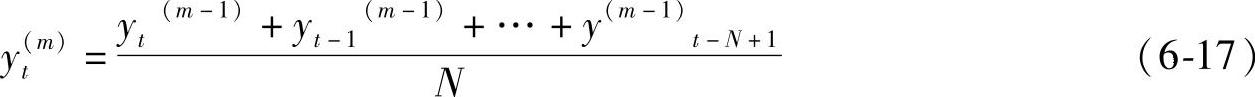
第二次移动平均预测方程:
对于线性倾向的数据,可以采用线性方程模型预测

其中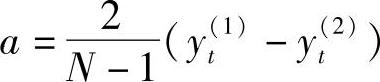 ,b=2yt(1)-yt(2)。
,b=2yt(1)-yt(2)。
2.加权指数平滑预测法
(1)基本概念 加权指数平滑预测法是移动平均法改进。它对各个时期历史数据以不同权值,反映对不同时期发生的数据在预测中起的不同作用。距预测期较近的数据,对预测值影响较大,因而其权值较大;距预测期较远的数据,对预测值影响较小,因而其权值较小。
加权指数平滑预测法需进行三次移动。第一次移动平均是基础,所得数据也可用于预测;第二次移动平均数据用于建立线性模型,进行线性趋势预测;第三次移动平均数据用于建立非线性模型,进行非线性趋势预测。
(2)一次移动平均加权指数平滑值的计算及预测模型
yt(1)=αyt+(1-α)yt-1(1) (6-19)
式中,yt(1)是第t期(如年份、月份等)的一次指数平滑值;yt是第t期的实际值或原始数据;α是平滑系数,0<α<1。
一次指数平滑预测公式
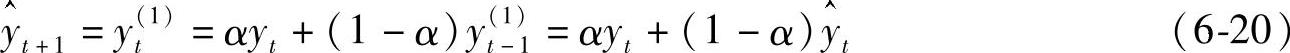
式中,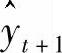 是第t+1期的预测值;
是第t+1期的预测值;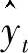 是第t期的预测值。
是第t期的预测值。
一次指数平滑预测法也是一种加权预测法,加权系数为α。它既不需要存贮全部历史数据,也不需要存贮一组数据,从而可以大大减少数据存贮问题,甚至只需要一个最新观察值、最新预测值和加权系数α,就可以进行预测。
把公式(6-20)进行展开,可以得到以下结果
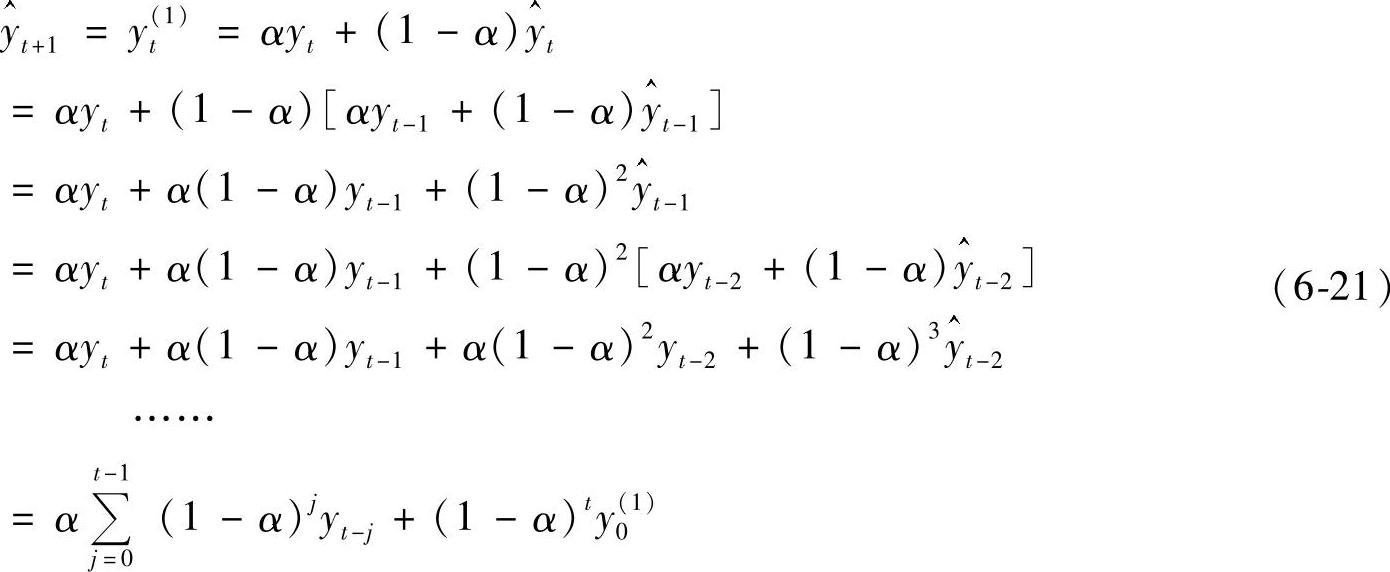
由上式可见,在计算yt(1)时,所有的资料数据yt都利用了。但是,各个yt在yt(1)中发挥的作用是不一样的。近期数据权重大,远期数据权重小。随着时间向过去推移,各期实际值对预测值的影响按指数规律递减。这就是为什么该方法称之为加权指数的原因。
在利用公式(6-21)进行预测时,需要确定初值y0(1)。初值y0(1)的选取可以采用以下两种方法:
当样本为大样本时,一般取时间序列的首项;当样本为小样本时,一般取时间序列的前几项求简单平均数。
一次移动平均加权指数平滑预测法具有方法简单的特点,但缺点是寻找最佳的加权系数α比较困难。这需要反复试验,才能保证预测的均方差最小。
(3)二次移动平均加权指数平滑值的计算及预测模型 上面介绍的一次指数平滑法虽然克服了移动平均法的两个缺点,但当时间序列的变动出现直线趋势时,用一次指数平滑进行预测,仍存在明显的偏差,因此需要修正。方法是在一次加权指数平滑的基础上,再做二次指数平滑,其计算公式为
 (https://www.chuimin.cn)
(https://www.chuimin.cn)
式中,α是加权系数,0≤α≤1。
由二次指数平滑法得到的数据可以建立线性预测模型计算公式

其中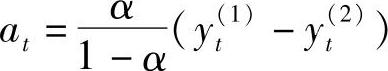 ,bt=2yt(1)-yt(2),T就是预测周期。
,bt=2yt(1)-yt(2),T就是预测周期。
[案例] 根据表6-7提供的2025年至2025年观察数据,预测2025年和2025年数据(α=0.8)。
表6-7 2025年至2025年观察数据

(续)
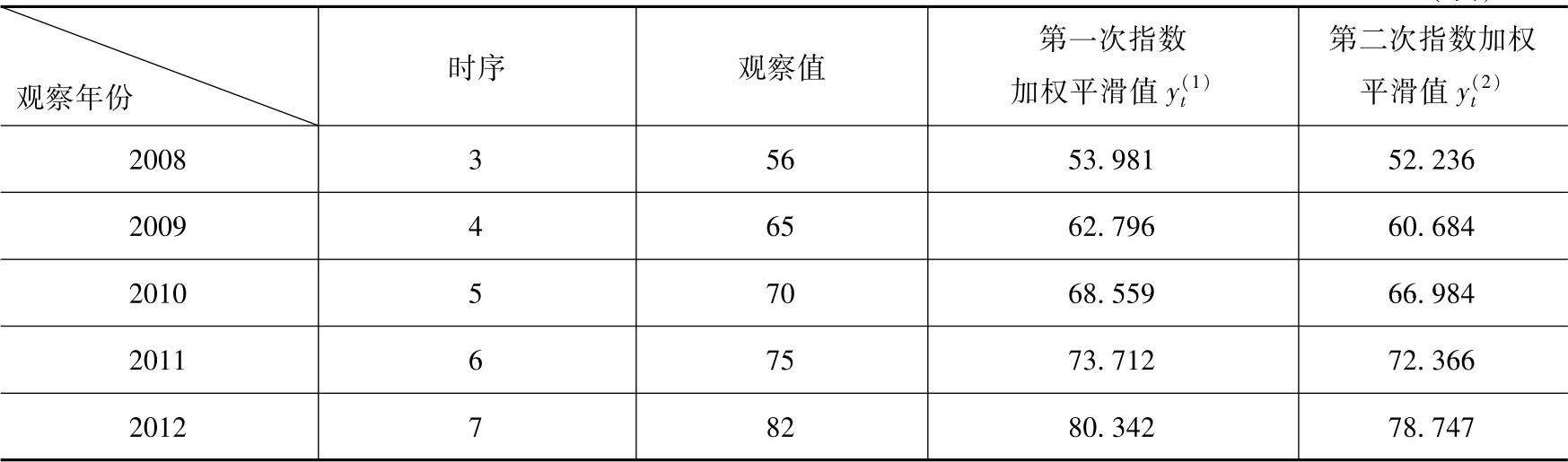
解:
首选确定初值y0(1)。由于本题目提供的样本数据较少,故初值取时间序列前三项的均值,即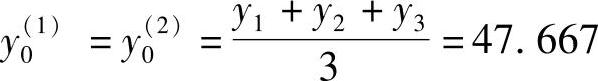
则把相关数据代入公式(6-22)中,分别得到一次指数平滑数据和二次平滑数据,其中
y1(1)=αy1+(1-α)y0(1)=0.8×40+0.2×47.67=41.534
y1(2)=αy1(1)+(1-α)y0(2)=0.8×41.534+0.2×47.67=42.761
其他数据见表6-7所示最右两列。
再由一次指数平滑数据和二次平滑数据,计算预测公式中的常系数a7和b7:
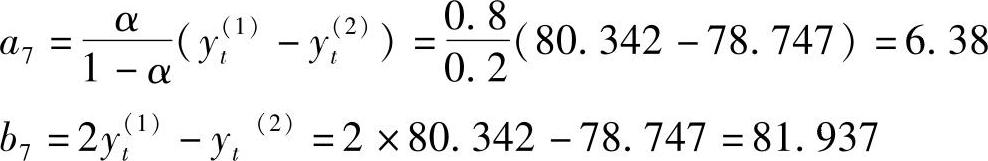
所以预测公式为
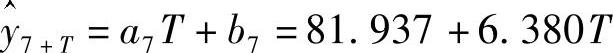
2025年和2025年的预测值分别为
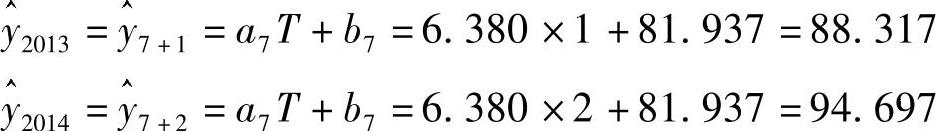
(4)三次移动平均加权指数平滑值的计算及预测模型 当时间序列为非线性增长时,一次指数平滑预测法和二次指数平滑预测法都将失去有效性。此时需要使用三次移动平均加权指数平滑法,并建立预测公式,其计算公式如下
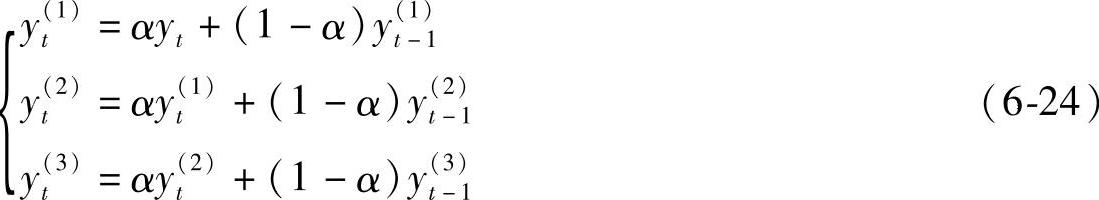
其中α是加权系数,0≤α≤1。
三次移动平均加权指数平滑法建立的预测模型是非线性的、抛物线模型,其计算公式为

其中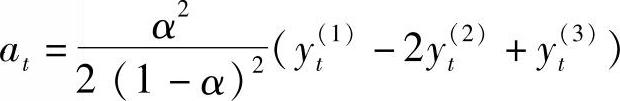 ,
,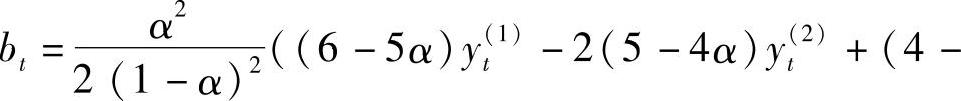
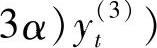 ,ct=3yt(1)-3yt(2)+yt(3)
,ct=3yt(1)-3yt(2)+yt(3)
公式中初始值y0(3)的选取和y0(1)、y0(2)的估算一样。即:
①当原始数据较多时,y0(1)=y0(2)=y0(3)=y1
②当原始数据较少时,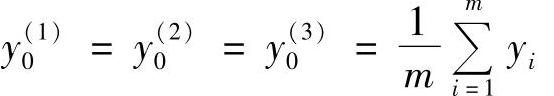
[案例] 某村历年农业纯收入数据见表6-8。试用加权平滑法预测该村2025年纯收入。
解:
①画数据曲线。如图6-8所示,纯收入随时间呈非线性关系。故采用三次指数加权非线性模型预测。
②选择加权系数。α=0.2
③初始值估算
由于原始数据较少,只有20个,所以初始值取前三个数的均值
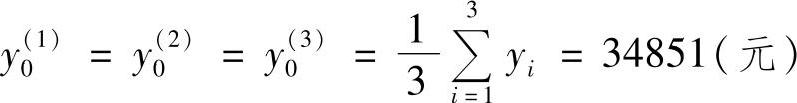
④计算各时间的三次加权平滑值。计算结果见表6-8。
表6-8 原始数据及三次加权平滑值
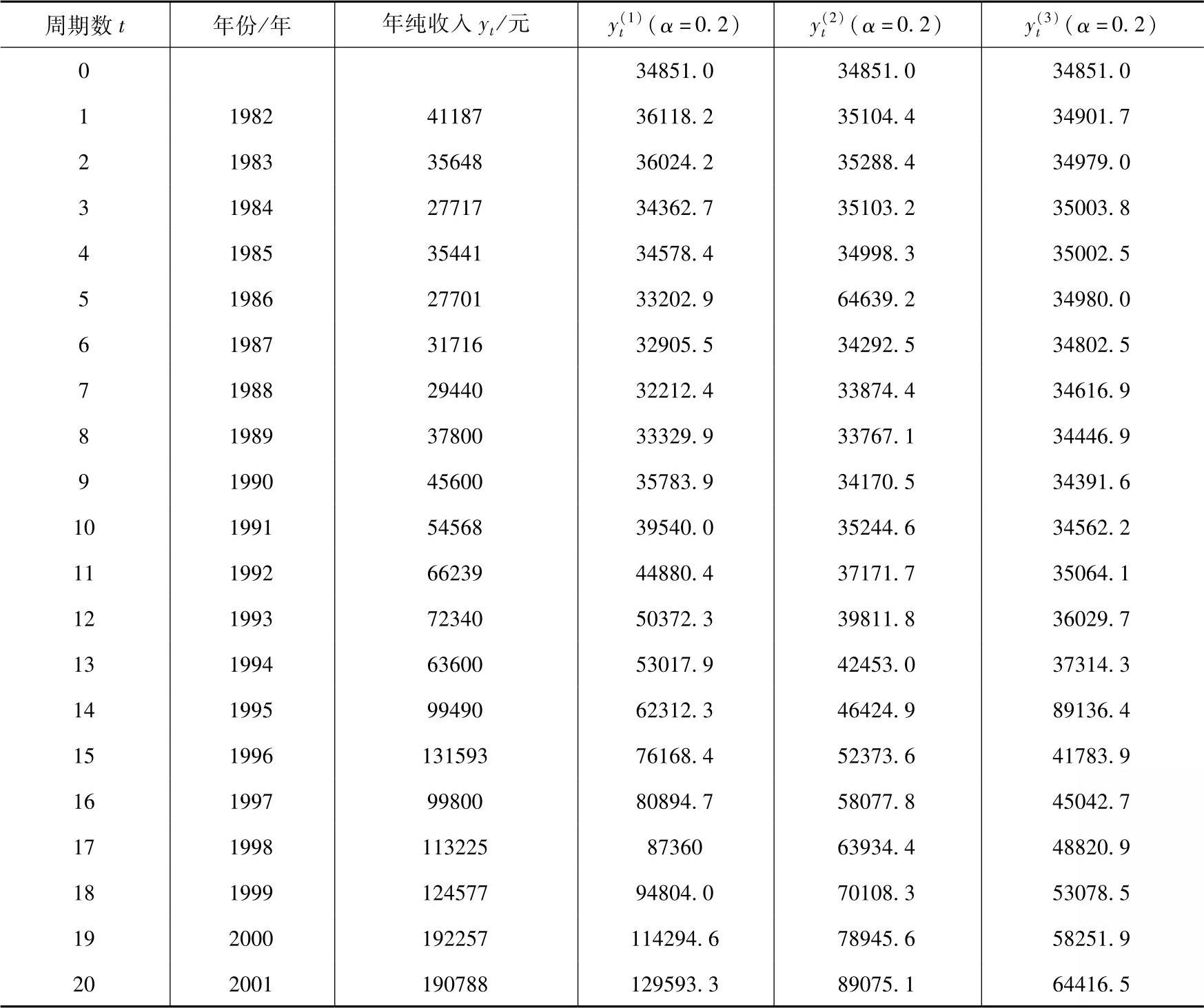
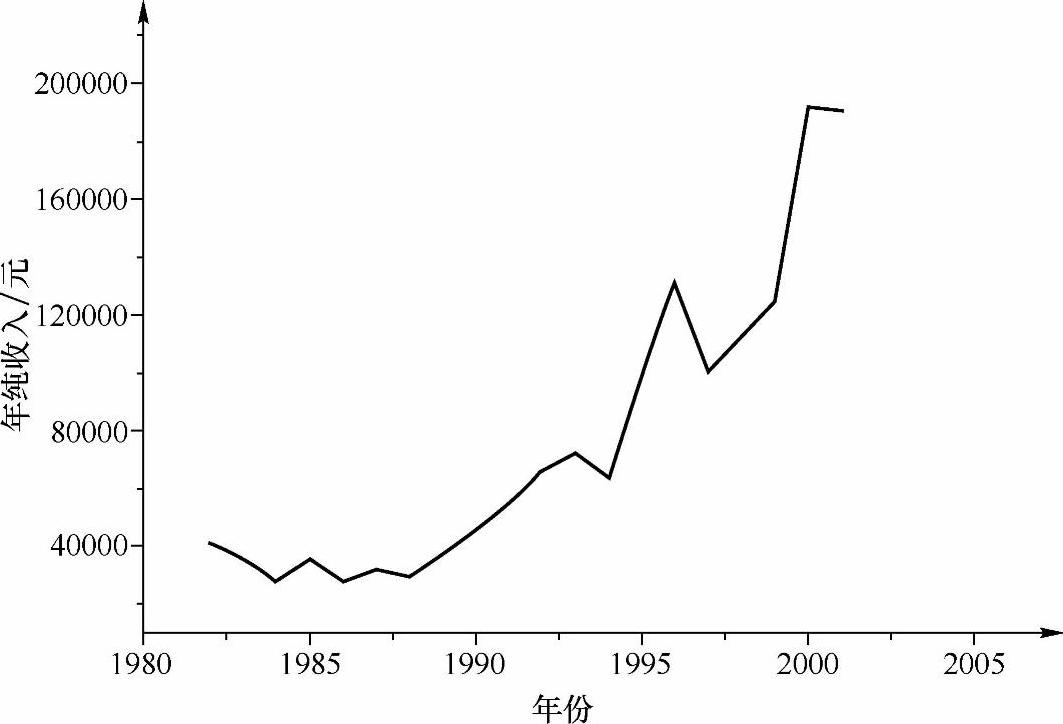
图6-8 纯收入随时间变化关系
⑤建立非线性方程

⑥预测2025年的纯收入
y2005=y2001+4=a2001T2+b2001T+c2001=495.6T2+18555T+185971.4=268121(元)
相关文章

移动平滑法就是对所取得的统计数据逐点推移,分段平均,以期最后得到一组具有较明显趋势的新数据。移动平滑法的预测程序框图见图9.2。图9.2移动平滑法的预测程序框图 某灌区历年人均林果产值见表9.3,试用移动平滑法建立预测模型,并求1999—2005年该灌区人均林果产值的预测值。图9.3人均林果产值的自然曲线及移动平滑预测曲线图由图9.3可知,对于直接用一次或二次移动平滑模型预测会出现滞后现象。......
2025-09-29

情景分析预测法就是在长期预测时,能够辨识关键因素及其影响方法。情景分析预测法具体有未来分析法、目标展开法和间隙分析法。图6-7 情景预测法的工作步骤[案例] 用情景预测分析法预测我国GDP发展趋势1.确定主题预测国内生产总值发展趋势。因为2006年与2005年相比,增长速度为23.9%,故以此作为情景A,对此迸行运算,可得2007年国内生产总值的预测值。......
2025-09-29

企业通过市场调查分析和预测产品的需求量、销售量、市场占有率及市场潜力等。市场调查预测法包括典型调查推算法、抽样调查推算法和全面市场调查法。也有学者把市场调查预测法划分为:用户需求意见调查预测法、业务人员意见调查预测法和经理人员意见调查预测法。......
2025-09-29

由于注塑件缺陷图解预测法的使用具有广泛性和普遍性,又不需应用相应计算机软件的特点,故图解法可以在CAE法不能使用的领域中充分发挥其作用。因为注塑件缺陷的预测分析,可以将大部分或全部的注塑件成型加工缺陷阻挡在注塑模结构方案制订之前。......
2025-09-29

1946年雷兹纳指出,饱和指数在预测水质性能时经常出现错误的判断。因此,他提出用经验式代替饱和指数,并把的差值称作稳定指数。雷兹纳通过实验,提出了经验的稳定指数IW来进行碳酸钙垢析出的判断,定义如下:pHY可由式计算:式中 M——水中总碱度,mmol/L雷兹纳稳定指数的判断方法见表2-20。表2-20 雷兹纳稳定指数判断标准IB和IW两个指数,只能用于判断碳酸盐结垢或腐蚀的倾向性,不能提供有关计算数据,故有它的局限性。......
2025-09-29

交叉概率法是对在交互影响因素作用下的事物进行预测的一种定性预测技术。交叉概率法是一种较先进的系统预测技术,在1968年,由Hayward和Cordon共同提出。而交叉概率法可以克服这个缺点。交叉概率法用于确定一系列事件Ei(i=1,2,…5)确定修正后的主观概率。[案例] 举例说明交叉概率预测方法现以美国能源政策评价预测分析来说明交叉概率法的使用。在表6-4中向上的箭头表示正方向的交叉影响,它表明该事件的发生将增加另一事件发生之概率。......
2025-09-29

装配尺寸链的封闭环就是装配后的精度或技术要求。在建立装配尺寸链时,首先应明确封闭环,即将装配精度要求定为封闭环;然后通过对装配关系的分析,即可查明其相应的装配尺寸链的组成环。因此,应分别建立产品部件装配的尺寸链和总装的尺寸链。不论哪种装配尺寸链,其解算的基本方法均有两种:极值法和概率法。......
2025-09-29

在接收端,将收到的预测误差的码字解码后再与预测值相加,得到当前像素值。在视频编码中,根据预测像素选取的位置不同,预测编码可分为帧内预测和帧间预测两种。在帧内预测编码时,选取的预测像素位于要编码像素同一帧的相邻位置;而帧间预测编码时,则选取时间上相邻的像素进行预测。......
2025-09-29
相关推荐