运筹学：操作研究的优化方案

2023-07-15 理论教育版权反馈

【摘要】：Operation Research原意是操作研究、作业研究、运用研究、作战研究，译作运筹学，它借用了《史记》“运筹策于帷幄之中，决胜于千里之外”一语中“运筹”二字，既显示其军事起源，又表明它在我国已早有萌芽。2）运筹学是依据给定目标和条件从众多方案中选择最优方案的最优化技术。运筹学开展活动是从二次大战初期军事任务开始的。图2-21 运筹学工作步骤5）参考所获最优解，作出正确决策。

Operation Research（简称OR）原意是操作研究、作业研究、运用研究、作战研究，译作运筹学，它借用了《史记》“运筹策于帷幄之中，决胜于千里之外”一语中“运筹”二字，既显示其军事起源，又表明它在我国已早有萌芽。

作为一门现代科学，在二次大战期间首先在英美两国发展起来，有的学者把运筹学描述为就组织系统各种经营做出决策科学手段。由于运筹学研究的广泛性和复杂性，人们至今没有形成一个统一的定义。以下给出几种定义：

运筹学创始人P.M.Morse与G.E.Kimball在他们奠基作中给运筹学下的定义：运筹学是在实行管理的领域，运用数学方法，对需要进行管理问题统筹规划，做出决策的一门应用科学。

运筹学另一位创始人定义运筹学：管理系统的人为了获得关于系统运行的最优解而必须使用的一种科学方法。使用许多数学工具（包括概率统计、数理分析、线性代数等）和逻辑判断方法，研究系统中人、财、物组织管理、筹划调度等问题，以发挥最大效益。

其他学者给出的运筹学定义有：

1）运筹学是一种科学决策的方法。

2）运筹学是依据给定目标和条件从众多方案中选择最优方案的最优化技术。

3）运筹学是一门寻求在给定资源条件下，如何设计和运行一个系统的科学决策的方法。

4）运筹学就是利用计划的方法和多学科专家组成的队伍，把复杂的功能关系表示成数学模型，其目的是通过定量分析为决策和揭露新问题提供数量依据。

5）运筹学是研究用科学的方法解决在资源不充分的情况下如何最好地设计人—机系统，并使之最好地运行的一门学科。

6）运筹学是运用科学方法（特别是数学方法）来解决那些在工业、商业等大型系统的指挥和管理方面出现的问题，目的是帮助管理者科学地决定其策略和行动。

7）运筹学是应用分析、试验、量化方法，对经济管理系统中人、财、物等有限资源进行统筹安排，为决策者提供有依据最优方案，以实现最有效地管理。

8）运筹学运用模型化方法，将一个已确定研究范围现实问题，按提出预期目标，将现实问题中的主要因素及各种限制条件之间的因果关系、逻辑关系建立数学模型，通过模型求解来寻求最优方案。

运筹学（OR）开展活动是从二次大战初期军事任务开始的。当时迫切需要把各项稀少资源以有效方式分配给各种不同军事经营及在每一经营内各项活动。美国及随后美国军事管理当局号召大批科学家运用科学手段处理各种战略与战术问题，开展研究的这些科学家小组就是最早运筹小组。

在二次大战中，“OR”成功解决了许多重要作战问题，显示了运筹科学巨大物质威力，为“OR”发展铺平道路。战后，与日俱增复杂性和专门化所产生问题，基本与战争中所面临问题类似，只是环境不同。于是，运筹学潜入工商企业和其他部门，并在20世纪50年代后得到广泛应用，形成了比较完备的一套理论，如规划论、排队论、存储论（又称库存论）和决策论等等。加上计算机问世，促进了运筹学发展。美国在1952年成立了运筹学会，并出版了期刊《运筹学》，世界其他国家也先后创办了运筹学会与期刊，在1957年成立了国际运筹学协会。

如图2-21所示，运筹学应用的具体程序处理问题分如下五个步骤：

1）收集资料，归纳问题。

2）建立相应数学模型。

3）编制计算机程序，求解模型。

4）检验和评价模型解。

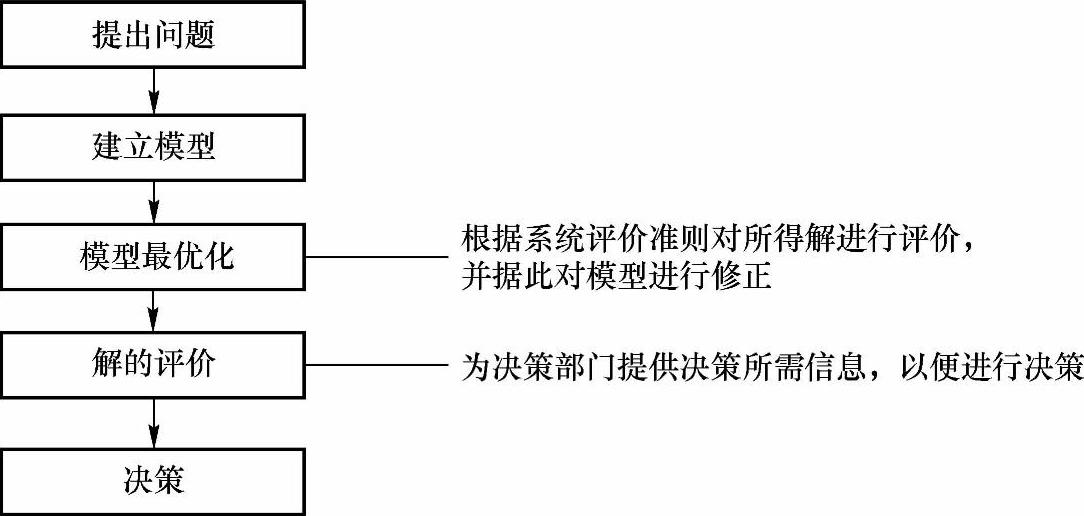
图2-21 运筹学工作步骤

5）参考所获最优解，作出正确决策。

运筹学主要分支：规划论、对策论、存储论或库存论、排队论、可靠性理论网、图与网络理论等。

2.7.1.1 规划论

数学规划即规划论，是运筹学的一个重要分支。早在1939年前苏联的康托洛维奇（H.B.Kahtopob）和美国的希奇柯克（F.L.Hitchcock）等人就在生产组织管理和制定交通运输方案方面首先研究和应用了规划论。1947年旦茨格等人提出了求解线性规划问题的单纯形方法，为线性规划的理论与计算奠定了基础。电子计算机的出现和日益完善，更使规划论得到了迅速的发展，从解决技术问题的最优化，到工业、农业、商业、交通运输业以及决策分析部门都可以发挥作用。因而具有适应性强，应用面广，计算技术比较简便的特点。非线性规划的基础性工作则是在1951年由库恩（H.W.Kuhn）和塔克（A.W.Tucker）等人完成的，到了20世纪70年代，数学规划无论是在理论和方法上，还是在应用的深度和广度上都得到了进一步的发展。

规划论的特点：

规划论是研究对有限资源进行统一分配、全面安排、统筹规划，以取得最好效果的一种数学理论。规划论的研究对象是计划管理工作中有关安排和估值的问题，解决的主要问题是在给定条件（或称约束条件）下，按某一衡量指标（或称作“目标函数”）来寻找最优方案。

数学规划和古典的求极值的问题有本质上的不同，古典方法只能处理具有简单表达式和简单约束条件的情况。而现代的数学规划问题的目标函数和约束条件都很复杂，巨要给出某种精确度的解答，因此算法的研究受到特别重视。

规划论方法主要包括：线性规划、非线性规划和动态规划等。

1.线性规划

最简单的一种规划问题就是线性规划。如果约束条件和目标函数都呈线性关系的就叫线性规划。要解决线性规划问题，从理论上讲都要解线性方程组，因此解线性方程组的方法，就是线性规划中非常必要的工具。

线性规划的解法——单纯形法的出现，对运筹学的发展起了重大的推动作用。许多实际问题都可以化成线性规划来解决，而单纯形法是一个行之有效的算法，加上计算机的出现，使一些大型复杂的实际问题的解决成为现实。

一般线性规划数学模型：

要求目标函数实现最大化（或最小化）

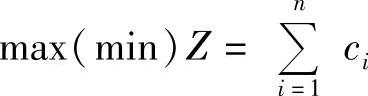
由m种有限资源构成的一组约束条件

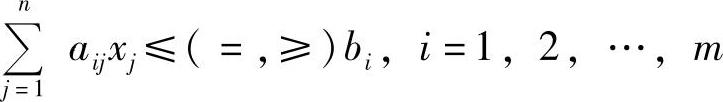
各变量不能取负值，即

x_j≥0，j=1，2，…，m

以上模型的形式表示要在限定的约束条件下求得目标函数的最优解。

2.非线性规划

许多实际问题如设计问题、经济平衡问题都属于非线性规划的范畴。在所考虑的数学规划模型中，目标函数与约束条件都是非线性。如果决策变量中要求取值必须满足整数线性规划问题，称整数规划。凡规定决策变量只能取值0和1的特殊整数规划，称0—1规划。

3.动态规划

动态规划是研究具有时间性的多阶段规划问题，使总效果最优的数学理论和方法。求解时，将一个复杂多段决策问题分解为若干个相互关联较易求解的子决策问题，然后寻求最优决策。比如研究经营管理、水源资源多级分配优化问题。还有在工程控制、技术物理和通信中的最佳控制问题中，动态规划已经成为经常使用的重要工具。

2.7.1.2 对策论

对策论运用数学方法，研究有利害冲突双方在竞争性活动中是否存在一方制胜他方的最优对抗策略，并研究如何找出这些策略的问题。最初用数学方法研究对策论是在国际象棋中开始的——如何确定取胜的方法。由于是研究双方冲突、制胜对策的问题，所以这门学科在军事方面有着十分重要的应用。数学家还对水雷和舰艇、歼击机和轰炸机之间的作战、追踪等问题进行了研究，提出了追逃双方都能自主决策的数学理论。随着人工智能研究的进一步发展，对博弈论提出了更多新的要求。

如果决策者的对方也是人（一个人或一群人），巨双方都希望取胜，那么这类具有竞争性的决策称为对策或博弈型决策。构成对策问题的三个根本要素是：局中人、策略与一局对策的得失。对策问题一般可分为有限零和两人对策、阵地对策、连续对策、多人对策与微分对策等。目前，决策论在政治、军事、经济等领域内得到了广泛应用。

2.7.1.3 存储论或库存论

存储论是一种研究物质最优存储及存储控制的理论。如果物质存储过多，则会占用大量仓储空间，增加保管费用，使物质过期报废从而造成经济损失；如果存储过少，则会因失去销售时机而减少利润，或因原料短缺而造成停产。因而如何寻求一个恰当的采购，存储方案就成为库存论研究的对象。

库存论利用应用数学方法研究在什么时间、多少数量、什么供应渠道来补充储备和什么方式出库，使得在保证生产正常运行情况下，保持库存和补充采购总费用最少。

2.7.1.4 决策论

决策论研究决策问题基本理论和方法。其主要研究内容：通过对系统状态信息处理，并对这些信息可能选取的策略、采取这些策略对系统状态所产生后果进行综合研究，以便按照某种衡量准则，选择出一个最优策略。

决策理论分传统决策理论和现代决策理论。传统决策理论是建立在安全逻辑基础上一种封闭式决策模型，把决策人看作具有绝对理性“经济人”（即以利己为动机，力图以最小的经济代价去追逐和获得自身的最大经济利益。），决策时会本能地遵循最优化原则来选择实施方案。而现代决策理论在决策时对各种客观因素和各种可能采取策略以及这些策略可能对系统状态造成后果进行综合研究，然后按照某种衡量准则，确定出一套切合实际衡量准则，使人们按照这些衡量准则，选择出一个满意策略。

2.7.1.5 排队论

因为排队现象是一个随机现象，因此在研究排队现象的时候，主要采用的是研究随机现象的概率论作为主要工具。如图2-22所示，排队论把它所要研究的对象形象的描述为顾客来到服务台前要求接待服务。如果服务台已被其他顾客占用，那么就要排队。另一方面，服务台也时而空闲、时而忙碌。这就需要通过数学方法求得一定服务率顾客的等待时间、排队长度等各种参数，以便求得更好的服务。

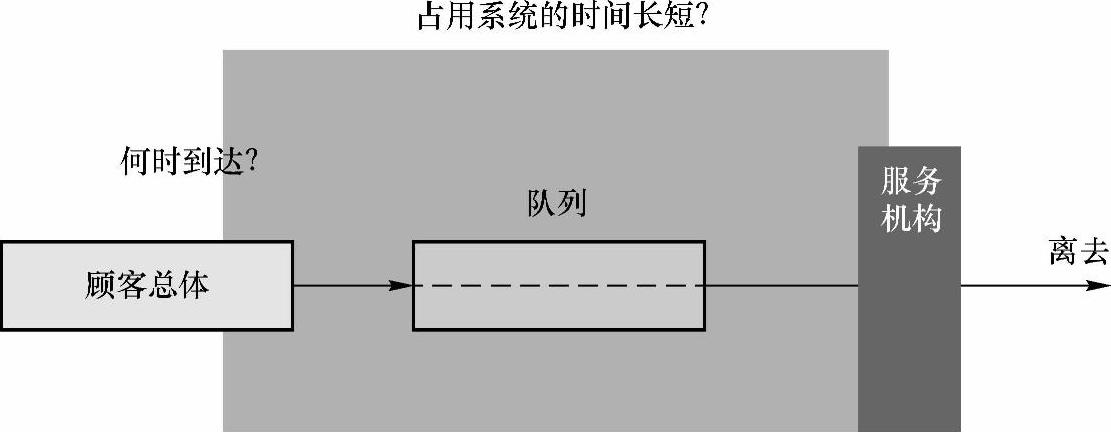
图2-22 排队论模型

排队论研究排队现象统计规律性，用以指导服务系统最优设计和最优经营策略，又称随机服务系统理论。通过对每个个别随机服务现象统计规律研究，找出反映这些随机现象平均特性规律，从而在保证较好经营效益前提下改进服务系统工作能力。

1909年丹麦电话工程师爱尔朗从电话交换机的效率问题开始研究排队问题，并在1930年开始对更为一般排队情况的研究。1949年，专家和学者们开始对机器管理、陆空交通等方面进行研究，1951年以后，排队论理论研究工作有了新进展，逐渐奠定了现代随机服务系统理论基础。排队论在工程中的应用是相当广泛的，比如水库水量的调节、生产流水线的安排、电网的设计，等等。

2.7.1.6 图与网络

图论创始人是数学家欧拉。1736年发表图论方面第一篇论文，解决著名哥尼斯堡七桥难题，相隔一百年后，在1847年基尔霍夫第一次应用图论原理分析电网，从而把图论应用到工程技术领域。自20世纪50年代以来，图论理论得到了进一步发展，并将复杂庞大工程系统和管理问题用图描述，解决了很多工程设计和管理决策最优化问题。例如，完成工程任务时间最少、距离最短、费用最省等等。可以说图论受到了数学、工程技术及经营管理等各方面广泛重视。

网络理论是利用网络图把庞大复杂工程项目各个环节合理衔接起来，使之相互协调，以实现工程项目在时间和费用上达到最优目标的一种理论和方法。

网络可以分为物质流网络、信息流网络和时间流网络等。

水、气、油、电、车辆、船舶、飞机、产品等物质，分别在自来水系统、输油输气管道系统、电网系统、交通运输系统、工厂的生产系统中流转，就构成了物质流网络。这类网络问题的优化包括求最大流问题、最小费用最大流问题等。

信息在广播通信系统、情报系统、计算机系统以及工程控制系统中的信息流程图中流转，就构成了信息流网络。

如果在各种网络图的各条边上标以完成工作所需要的时间，这样的网络图就构成时间流网络。通过网络图绘制和网络时间参数计算，可以估计影响进度和资源利用的各种因素，做到统筹规划、合理安排和使用资源，从而保证顺利完成工程项目预定目标。网络理论主要应用于大型复杂工程系统。

运筹学：操作研究的优化方案

相关推荐