不失一般性，我们假设在0时刻其值为1，因此，到时刻t（≥0），保险公司的盈余过程可表示为：Tang等在F∈R以及｛L；t≥0｝与｛Xk；k≥1｝，｛θk；k≥1｝相互独立的条件下，建立了模型（2.1）的破产概率的渐近估计。在索赔额｛Xk；k≥1｝与索赔发生时间间隔｛θk；k≥1｝具有一定相依结构的条件下，给出本节的主要结论。......
2023-07-06
带随机投资收益的二维重尾时依更新风险模型破产概率的渐近估计优化方案
【摘要】：本节考虑一类特殊的二维风险模型，其中两家保险公司共同承保标的（联保），并按δ1和δ2的比例承担索赔。为简单起见，假设两家保险公司只共同经营一种保险业务，且每个保险公司都有自己的投资策略，即每个保险公司的随机投资收益可能不同。这就意味着文中的随机投资收益R1和R2事实上也都是无风险投资与风险投资的组合。表3-1和3-2展示了在不同初始资金和分保比例情况下的数值模拟结果。至此，引理3.3证毕。
本节考虑一类特殊的二维风险模型，其中两家保险公司（或同一家保险公司的两个分公司）共同承保标的（联保），并按δ1和δ2（δ1+δ2=1）的比例承担索赔。为简单起见，假设两家保险公司只共同经营一种保险业务，且每个保险公司都有自己的投资策略，即每个保险公司的随机投资收益可能不同。因此，到时刻t（≥0）为止，第i家（i=1，2）保险公司的盈余过程为
本节的主要结论如下所示。
金融市场投资往往包括无风险投资和风险投资，且保险公司往往将其盈余的一部分（比如说比例ζ∈［0，1］）进行有风险投资，而将剩下的部分进行无风险投资。这就意味着文中的随机投资收益R1（t）和R2（t）事实上也都是无风险投资与风险投资的组合（见Hao和Tang（2012），Heyde和Wang（2009））。特别地，如果ζ=0，这就是说两个保险公司都仅进行无风险投资，因此我们立即有如下结论。
推论3.1 考虑如（3.11）所示的二维风险模型，其中两家保险公司都将其资金进行利息力为r（＞0）的债券投资（也就是说其中的R1（t）和R2（t）都变成rt）且F∈R-α（α＞0），那么在定理3.2的条件下，对所有满足P（τ1≤T）＞0的0＜T＜∞，有
注3.3 Hu和Jiang（2013）在聚合风险模型为具有正则变尾的复合Poisson过程以及常利息力的条件下，考虑了模型在x2/δ2≥x1/δ1条件下的渐近破产概率。显然，定理3.2和推论3.1中都允许索赔与索赔发生时间间隔相依，将先前的结论推广到了一个更现实和实用的环境中，具有一定的理论和现实意义。
接下来我们通过数值模拟方法说明所得渐近表达式的精确性。我们首先将Lévy过程退化为线性过程rt（常利息力r＞0），然后将投资收益看成为一般的几何布朗运动，即R1（t）=R2（t）=νt+σW（t），其Laplace指数为ø（z）=-νz+
，其中ν∈R，σ＞0，｛W（t）｝为一标准布朗运动。
考虑索赔额分布为Pareto分布F（x；α，κ）=1-（κ/（x+κ））α，显然该分布属于R-α族。假设（X，θ）的相依性满足Farlie-Gumbel-Morgenstern copula函数关系，其中Farlie-Gumbel-Morgenstern copula的具体形式为：
索赔发生时间间隔｛θk；k≥1｝为一i.i.d.的随机变量序列，其共同分布是参数为λ的指数分布。由Li等（2010）可知，在上述条件下的（X，θ）满足假设A这一条件且其中的h（t）=1+γ（2e-λt-1），从而可得
当R1（t）=R2（t）=rt时，这说明保险公司将全部盈余进行无风险投资（比如债券），此时我们令参数α=1.5，κ=1，λ=0.5，γ=0.5，并分别在初始资金（x1，x2）=（10，20），（100，200）的条件下考虑模型（3.11）在有限时间（T=1）内的破产概率，其中常利息力r和保费收入率c分别为0.5和10。表3-1和3-2展示了在不同初始资金和分保比例情况下的数值模拟结果。
表3-1 初始资金（10，20）下模拟值与渐近估计值比较
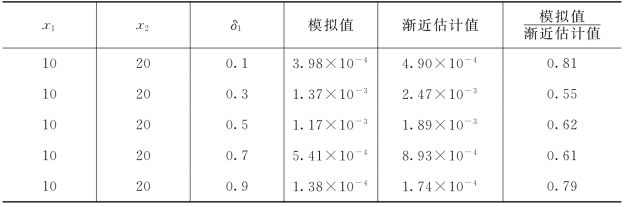
表3-2 初始资金（100，200）下模拟值与渐近估计值比较
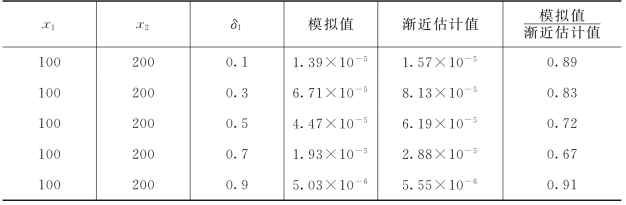
当R1（t）=R2（t）=νt+σW（t）时，这说明保险公司将其资产全都进行风险投资（比如股市投资）。显然，当σ=ν=1时，定理3.1中的条件都满足了。在其余各种参数同上文所述的情况下，我们也可得到两张数值模拟表格（表3-3和表3-4）。
表3-3 初始资金（10，20）下模拟值与渐近估计值比较
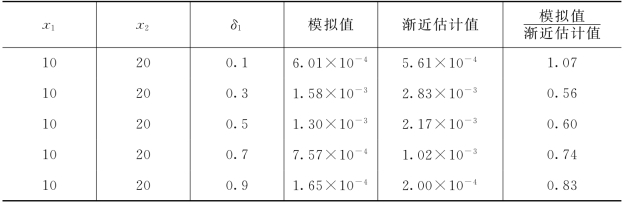
表3-4 初始资金（100，200）下模拟值与渐近估计值比较
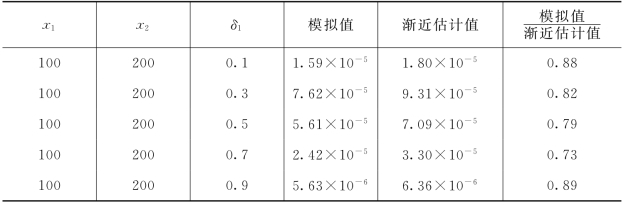
为了证明定理3.2，我们先给出一些引理。
引理3.3 令｛（Xk，θk）；k≥1｝是一i.i.d.随机对序列且与一般随机对（X，θ）同分布，在定理3.2的条件下，对任意固定的n和0＜T＜∞，有
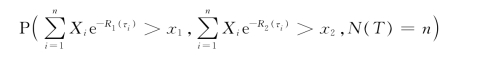
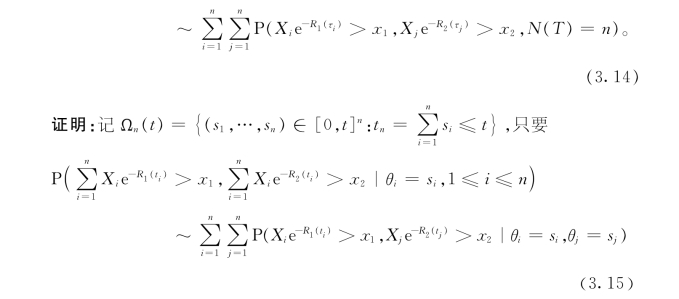
成立，就可得到
因此，为证引理成立，只要说明（3.15）式成立即可。
对任意的0＜ε＜1，我们有
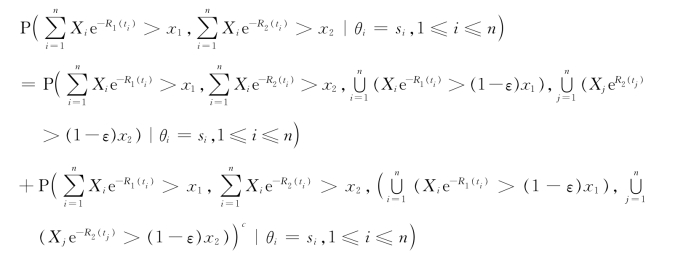
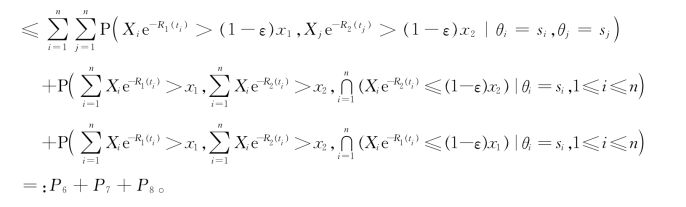
对于P6，显然又有
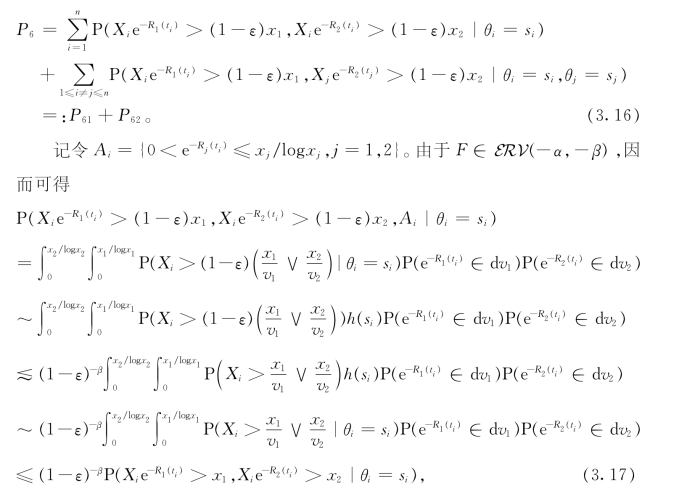
其中在第二步和第四步中利用了假设A。同时，从（3.17）式中的第二步可知
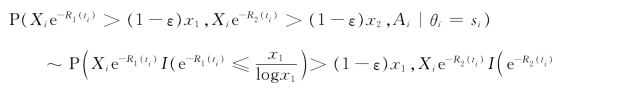
其中我们利用了对任意的b＞β，当y→∞时，都有
这一性质（该性质具体可见Tang和Tsitsiashvili（2003））。结合（3.17）式，就可推出
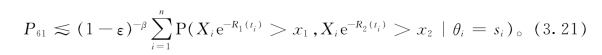
同P61的证明类似，我们有
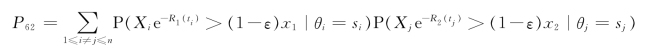
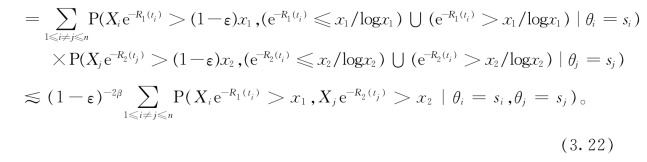
因此，根据（3.16）式、（3.21）式和（3.22）式可得
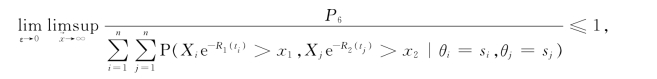
其中我们利用了不等式
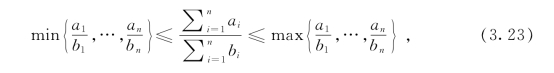
对所有的ai＞0和bi＞0，i=1，…，n成立。
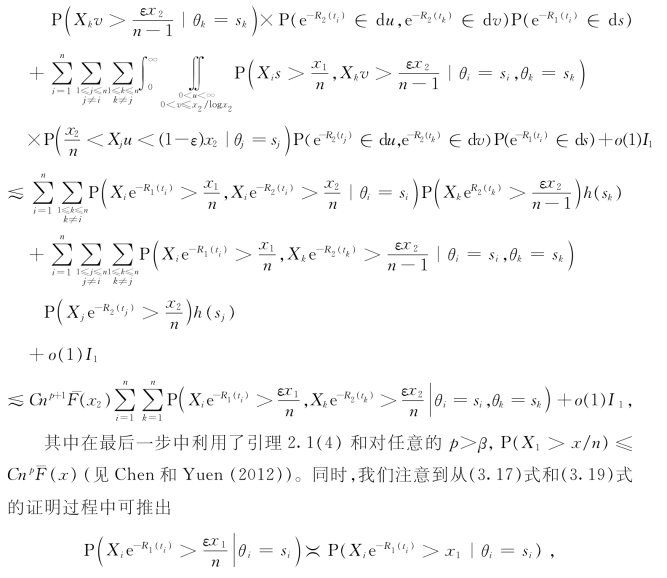
而由（3.22）式又可推出：对固定的n和i≠k，
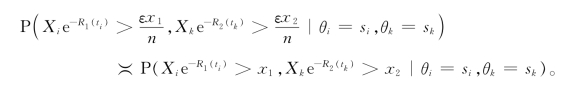
将上述两式和（3.23）式结合后可得
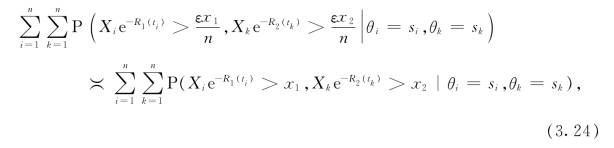
从而可得P7=o（1）P6。类似的，我们也可得到P8=o（1）P6。因此，先让→x→∞再让ε→0后就有
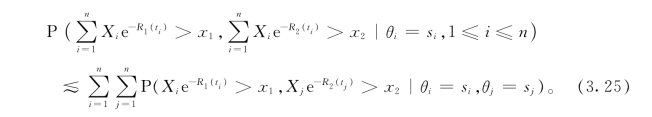
同时，对任意的0＜ε＜1，我们有
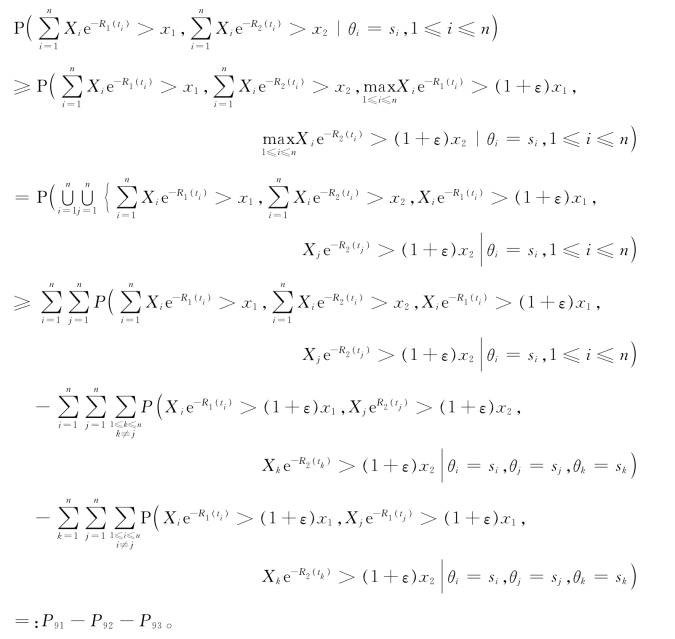
对这些非负随机变量，显然有
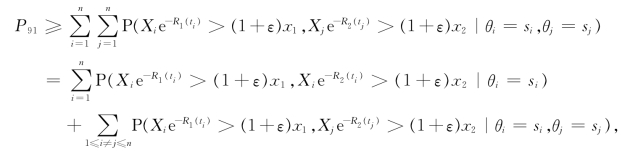
因而在（3.23）式的辅助下，采用和P6类似的证明方法后即有
由此再结合（3.25）式就可知（3.15）式成立。至此，引理3.3证毕。
注3.4 关系式（3.14）中的事件｛N（T）=n｝有可能概率为0，但我们仍旧采用这一渐近等价符号，这是因为当关系式a（x1，x2，T）～b（x1，x2，T）两边同时为0时，该符号就可看成是a（x1，x2，T）=（1+o（1））b（x1，x2，T）的简化。
引理3.4 令｛（Xk，θk）；k≥1｝是一i.i.d.随机对序列且与一般随机对（X，θ）同分布，则在定理3.2的条件下，对任意固定的n和0＜T＜∞，有
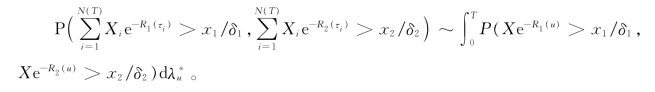
证明 首先任选一个正整数M，然后就有
其中在第六步中利用了
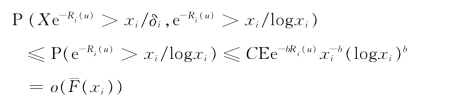
以及由（3.20）式和引理2.1（4）所推出的
因此就有
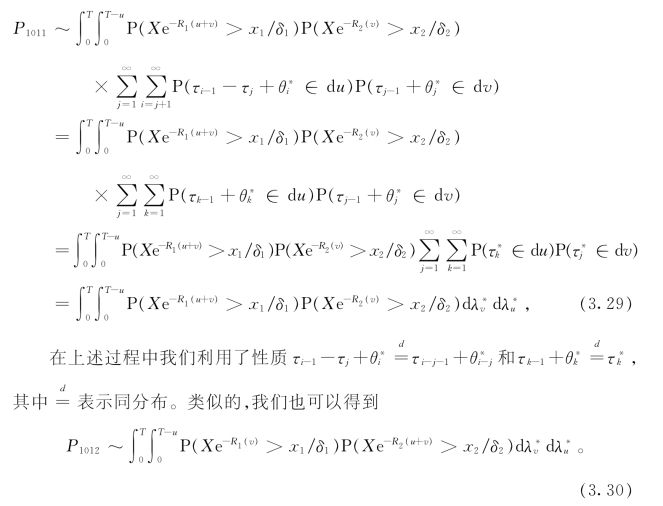
而对于P1013，又有
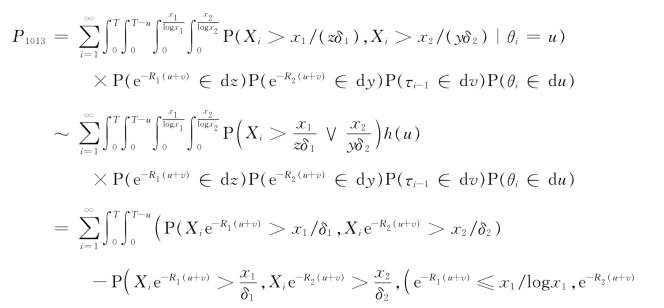
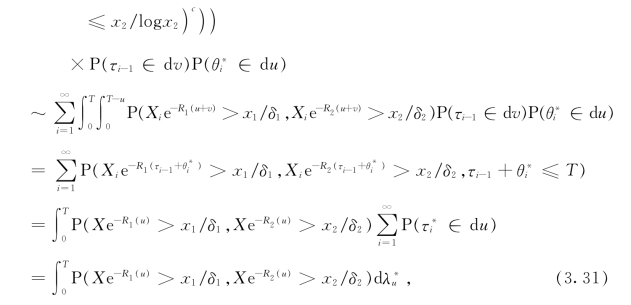
其中在第二步和第四步中分别利用了假设A以及由x1=O（x2）与x2=O（x1）所推出的
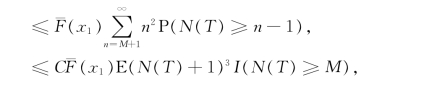
其中在第三步中使用了引理2.1（4），由此再结合x1=O（x2）与x2=O（x1）即可推出
此处的I（·）表示一示性函数。因此，由E（N（T））b＜∞（b＞0）即可推知
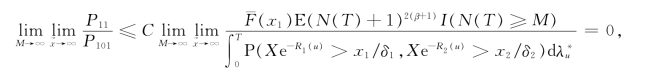
这就说明在先让→x→∞再让M→∞的条件下，P11=o（1）P10成立。引理3.4得证。
基于前面的引理准备，我们开始证明定理3.2。
定理3.2的证明 首先观察
由引理3.4可得
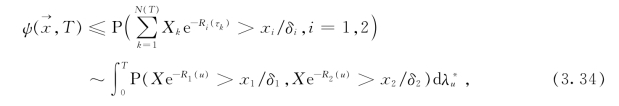
以及对0＜ρ＜1，
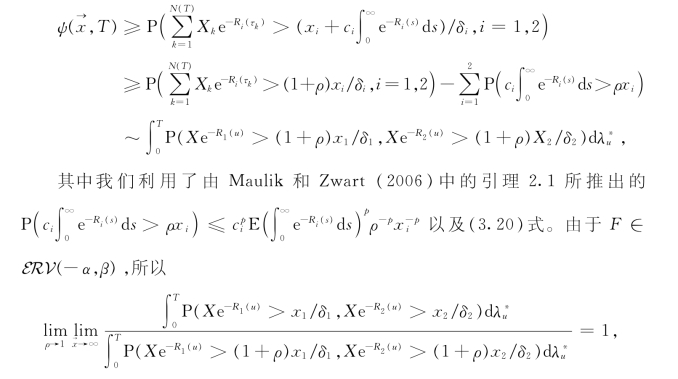
由此再结合控制收敛定理可得
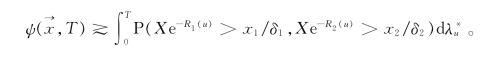
显然，由上式结合（3.34）式即得定理3.2成立。
注3.5 本节的主要结果及证明源自Fu和Yu（2018）。
有关若干重尾时依风险模型的渐近性质的文章
- 详细阅读
-
带副索赔的重尾时依更新风险模型破产概率的渐近详细阅读
类似地，我们对副索赔及其相应的延后时间也给出一定的相依结构假设。在本节中我们将考虑带副索赔的时依风险模型中的有限时和无限时破产概率的渐近估计。对于p QAI索赔额序列，在其共同分布属于ERV族以及索赔额与索赔发生时间间隔相互独立的条件下，Li对模型的最终破产概率给出了如下的渐近估计。同时，我们也打算将定理2.3从ERV族推广至更大的控制变尾族，并给出有限时和无限时破产概率的渐近估计。......
2023-07-06
-
带投资和副索赔的二维重尾时依更新风险模型的破详细阅读
显然，副索赔发生在其主索赔之后，且延后的时间是随机的。因此，两保险公司具有随机投资收益的盈余过程分别为由此定义两类有限时破产概率由于在现实中索赔额与索赔发生的时间间隔之间往往是存在着一定的联系，因此在本节中对主索赔和副索赔仍旧采用假设B和假设C。......
2023-07-06
-
精算学中风险模型对破产概率的估算与控制详细阅读
在精算科学中，精算学家通常会根据保险业务的历史数据所呈现的特征提出不同的风险模型，然后对风险模型的破产概率进行估算，并利用估计值的大小对整体风险进行度量以达到控制风险的目的。因此，我们给出有限时破产概率和无限时破产概率的定义。......
2023-07-06
-
精细的二维额度更新风险模型的大偏差详细阅读
在本节中，我们拟将式推广至二维更新风险模型，也就是说研究二维额度相依更新风险模型中索赔向量和的精细大偏差。注3.2 定理3.1在允许索赔与索赔发生时间间隔相依的条件下给出了总索赔额向量的精细大偏差公式，在一定程度上推广了定理2.5。......
2023-07-06
-
用频率估计概率的优化方法详细阅读
1．下列模拟掷硬币的实验中，不正确的是（ ）．A．用计算器随机地取数，取奇数相当于反面朝上，取偶数相当于硬币正面朝下B．袋中装两个相同的小球，分别标上1和2，随机地摸，摸出1表示硬币正面朝上C．在没有大小王的扑克中随机地抽一张牌，抽到红色牌表示硬币正面朝上D．将1，2，3，4，5分别写在5张纸上，并搓成团，每次随机地取一张，取到奇数号表示硬币正面朝上2．某小组在“用频率估计概率”的实验中，统计了某......
2023-07-03
-
二维连续型随机变量条件概率计算精要详细阅读
【主要内容】设二维连续型随机变量（X，Y）的概率密度为f（x，y），则两类条件概率P（a
2023-10-27
-
随机模拟：模拟事件出现及服务时间的随机概率详细阅读
将随机数作为事件出现的随机概率进行模拟工作步骤①求出模拟事件出现的概率。④从随机数表中任意指定一个随机数作为始点，一个一个的模拟。由于表7-5中分布概率、累计频率和随机概率只精确到小数点后两位数，所以获取的随机数只需两位数即可。表7-7 随机数与相应的服务时间3）将随机数加以改造，作为实际发生的事件进行模拟。目的是使模拟随机数的平均数与均方差和模拟事件的平均数与均方差相等。......
2023-07-15
相关推荐