中偏差问题的额度相依更新风险模型

2023-07-06 理论教育版权反馈

【摘要】：假设A中的相依结构式是在给定索赔发生之间的等待时间的条件下，通过索赔额的条件尾概率来描述的，所以此前的时依风险模型其实是等待时间的相依。因此，到t（≥0）时刻为止的索赔额总量可表示为一个复合过程式所描述的索赔额总量模型其实也可以看出一个基本的更新风险模型。类似的问题也曾被Shen和Zhang在基于顾客进入的风险模型以及Gao和Liu在标准更新风险模型中所研究过。

假设A中的相依结构式是在给定索赔发生之间的等待时间的条件下，通过索赔额的条件尾概率来描述的，所以此前的时依风险模型其实是等待时间的相依。Chen和Yuen（2012）提出了一种比假设A更为宽泛的相依性结构。

假设D 对于一般随机对（X，θ），存在一个非负随机变量θ*，对所有较大的x＞0，都可以使θ在（X＞x）的条件下被θ*随机控制；也就是说，存在某个x0＞0，使得对所有的x＞x0和t∈［0，∞）都有

该相依结构是在给定索赔额较大的情况下描述索赔发生等待时间的条件分布，因此在假设D下所构建的这类时依风险模型常被称为索赔额额度相依（size-dependent）风险模型。在假设A成立的情况下，当x→∞时，

对所有t∈［0，∞）一致成立。令V（d s）=h（s）P（θ∈d s），则由E h（θ）=1可知V是［0，∞）上一个适正的分布函数，从而可得P（θ＞t|X＞x）≤2¯V（t）。这样一来，我们就可构造一个分布为V0=（1-2¯V）∨0的随机变量θ*使得（2.26）式成立。这就说明假设D是一类较假设A更弱的相依结构。

考虑一个更新风险模型，其索赔额｛Xk；k≥1｝构成一i.i.d.（分布函数为支撑在［0，∞）上的F）的随机变量序列，索赔发生时间间隔｛θk；k≥1｝也构成一i.i.d（分布函数为支撑在［0，∞）上的G）的随机变量序列。记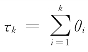 pagenumber_ebook=46,pagenumber_book=40 ，k∈N，为索赔发生时间，同时令τ0=0，由此构成了一个更新计数过程N（t）=sup｛n≥1：τn≤t｝，t≥0。因此，到t（≥0）时刻为止的索赔额总量可表示为一个复合过程

（2.27）式所描述的索赔额总量模型其实也可以看出一个基本的更新风险模型。

众所周知，大偏差是研究极值事件概率渐近性的重要工具，由于其在保险风险和排队论理论中的重要作用，越来越多的文献致力于重尾随机变量随机和的精细大偏差研究，具体可参见Klüppelberg和Mikosch（1997），Baltrūnas等（2008），Kaas和Tang（2005），Ng等（2003，2004），Tang等（2001），杨洋和王开永（2013）。需要指出的是，这些结论也都是建立在索赔额与索赔发生时间间隔独立的框架之下。

在假设D成立的条件下，Chen和Yuen（2012）对索赔额总量S（t）建立了如下的精细大偏差公式。

定理2.5 考虑索赔额总量模型（2.27），其中索赔额与索赔发生时间间隔所构成的i.i.d.随机对序列｛（Xk，θk）；k≥1｝与一般随机对（X，θ）同分布，且一般随机对（X，θ）满足假设D。如果F∈C，0＜E X=μ＜∞且0＜Eθ=λ-1＜∞，那么对任意给定的γ＞0，当t→∞时，

对所有x≥γt一致成立；也就是说，

我们注意到定理2.5中给出的x-区域为［γt，∞）。因此，我们自然会思考（2.28）式对其他x-区域是否成立；如果成立，还需要哪些条件呢？类似的问题也曾被Shen和Zhang（2012）在基于顾客进入的风险模型以及Gao（2007）和Liu（2010）在标准更新风险模型中所研究过。

在本节中我们将在额度相依条件下考虑索赔额总量模型的中偏差理论，也就是说我们将证明（2.28）式对x∈［γb（t），+∞）也成立，其中b（t）为一正值函数且满足b（t）/t→0（t→∞）。同时，在很多文献中都假设索赔额之间是相互独立的，显然这并不符合保险实务。本节的一个目标就是将定理2.5的结果推广至索赔额之间具有END结构这一复杂情况。

在下文中，记a（t）为一正值函数且对所有较大的t满足

其中［t］表示t的整数部分。本节的主要结论如下。

定理2.6 考虑如（2.27）式所示的索赔额总量模型，其中｛Xk；k≥1｝为一同分布的END随机变量序列且满足F∈C和存在某个α＞α′使得E|X1|α＜∞，｛θk；k≥1｝为一i.i.d.的随机变量序列且满足0＜Eθ1=λ-1＜∞。索赔额与索赔发生时间间隔｛（Xk，θk）；k≥1｝构成一同分布的随机对序列且与满足假设D和Eθ*＜∞的一般随机对（X，θ）同分布，同时假设对于不相同的i和j有Xi和θj相互独立这一性质。如果当t→∞时，

那么对任意固定的γ＞0，当t→∞时，

对于所有x≥γb（t）一致成立；也就是说

其中b（t）=a（λt）。

注2.7 当｛N（t）；t≥0｝为一齐次Poisson过程并且a（n）满足条件（2.30）

时，（2.31）式自然成立。同时，Gao（2009）和Liu（2010）中都给出了一些其他的非负整值计数过程｛N（t）；t≥0｝在某些a（n）下也都满足（2.31）式。因此，我们可以说（2.31）式对很多计数过程都能满足，是一个较为温和的条件。

注2.8 当a（n）=n1/α′（log n）2时，易证a（n）满足条件（2.30）和b（t）/t→0（t→∞）。这也直接说明我们的结论在一定程度上推广了定理2.5，因为定理2.5中的x-区域只是选取了［γt，∞）而已。

根据更新定理（Asmussen（2003）），我们有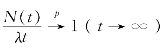 pagenumber_ebook=48,pagenumber_book=42 。因此在定理2.6中取a（n）=n即有如下的精细大偏差定理。

推论2.4 考虑如（2.27）式所示的索赔额总量模型，在定理2.6的条件下，对任意固定的γ＞0，当t→∞时，

对所有x≥γt一致成立。

根据假设D，先引入一个与其他变量都独立的非负随机变量，并令其与在（X＞x）这一条件下的θ具有相同的分布函数。相应地，记

并令

显然，｛N*（t）；t≥0｝为一延迟更新计数过程。如Chen和Yuen（2012）所说，的分布通过条件（X＞x）而与x相关，故｛N*（t）；t≥0｝的分布也是如此。我们首先介绍一个同延迟更新计数过程相关的引理。

引理2.8 如果（2.31）式成立，那么在假设D以及0＜Eθ*＜∞成立的条件下，对每个满足c（t）→∞（t→∞）的函数c（t）：［0，∞）→［0，∞），当t→∞时，

对所有x≥c（t）一致成立；也就是说，对任意的δ＞0，

这就意味着

以及

至于延迟更新计数过程｛N*（t）；t≥0｝，对所有x≥c（t），我们有

和

一致成立。由于Eθ*有限，则由（2.32）式和（2.33）式可知，当t→∞时，上述两式都趋向于0。这就说明当t→∞时，

对所有x≥c（t）一致成立。引理2.8得证。

除了引理2.8，如下两个引理在定理2.6的证明中也至关重要，它们分别源自Liu（2010）中的定理2.1以及稍加修改后的Koˇcetova等（2009）中的定理1（i）。

引理2.9 令｛Xk；k≥1｝为一列具有共同分布F∈C的END随机变量序列，如果存在某一α＞α′使得E|X1|α＜∞，那么对任意固定的γ＞0，当n→∞时，

对所有x≥γa（n）一致成立，其中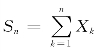 pagenumber_ebook=50,pagenumber_book=44 。

引理2.10 令索赔发生时间间隔序列｛θk；k≥1｝是一i.i.d.的非负随机变量序列，且其期望为1/λ∈（0，∞）。那么，对任意的δ＞0和某个c＞1，有

接下来开始证明定理2.6。

定理2.6的证明在下文中，每个极限都被看成是当t→∞时对所有x≥γb（t）成立。为了证明定理2.6，我们只要证明如下两个式子成立即可：

和

我们首先证明（2.34）式成立。令0＜δ＜1以及ν＞1为任意固定的常数，其中δ充分小。因此，我们可得

P(S(t)-μλt＞x)

其中Sn，i=Sn-Xi（n≥1，1≤i≤n）。

我们首先处理I13。由于λt-δb（t）≤n≤λt+δb（t），故在定理2.6的条件下，采用与Liu（2010）中（4.13）类似的证明方法以及利用F∈C和｛Xk；k≥1｝非负，我们可以得到对某个充分小且满足1-ν+δμγ-1＜0的正常数δ（令0＜δ＜γ（ν-1）μ-1即可），0＜ρ＜1和充分大的n，有

对所有x≥γa（n）一致成立。这也就意味着

在上述证明中我们利用了概率不等式P（A¯C|D）≥P（A|D）-P（C|D），其中A、C、D为任意三个随机事件。因此，由引理2.8、（2.29）式以及F∈C可知

至于I14，由END序列的相依性质可知

由此再结合（2.36）式即知（2.34）式成立。

接下来我们开始证明渐近上界。首先选取任意的0＜δ＜1，并将P（S（t）-μλt＞x）分成如下两部分：

P(S(t)-μλt＞x)

=P(S(t)-μλt＞x，N(t)≤λt+δb(t))+P(S(t)-μλt＞x，N(t)＞λt+δb(t))

=：I15+I16。

对I15，首先选择充分小的δ使其满足1-μδγ-1＞0，从而根据引理2.9可得

因此，结合F∈C和（2.29）式即有

这也验证了（2.35）式的合理性。定理2.6证毕。

注2.9 本节的主要结果及证明源自Fu和Shen（2017）。