基本符号及其变量的相依性

2023-07-06 理论教育版权反馈

【摘要】：定义1.3 称随机变量X1，…定义1.4 对于随机变量序列｛Xk；k≥1｝，如果对每个n和所有的x1，…，xn，都存在某一独立于n的正常数M，使得（1.5）式和（1.6）式同时成立，则称｛Xk；k≥1｝是广义负相依序列。定义1.5 两个非负随机变量X1和X2是拟渐近独立的，如果如果X1和X2同分布，那么就说它们是渐近独立。如果随机变量序列｛Xk，k≥1｝中的任意两个随机变量都是QAI的，则称｛Xk；k≥1｝是两两AQI序列。

对任意的分布函数F，记

定义另一个关于分布的有用参数，它在研究控制变尾分布时非常重要。对任意的分布函数F，记

显然，0≤LF≤1，且当F∈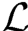 pagenumber_ebook=15,pagenumber_book=9 时，LF=1；当F∈D时，LF＞0。

由于索赔之间的独立性假设在保险实务中是不大合理的，因此我们引入一些保险精算中常用的相依结构。

定义1.3 称随机变量X1，…，Xn是负相伴（NA）的，若对｛1，2，…，n｝的任意两个非空不交子集A和B，均有

Cov(f(Xi，i∈A)，g(Xj，j∈B))≤0，

其中f和g是使上式有意义且对各变元不降的函数。对于随机变量序列｛Xk；k≥1｝，如果对任意的n≥2，X1，…，Xn是NA的，则称｛Xk；k≥1｝是NA序列。

负相伴的概念是由Ala m和Saxena（1981）和Joag-Dev和Pr oschan（1983）分别提出的，由于其在可靠性理论、渗透理论和多元统计分析中均有广泛应用而被人们所研究。

定义1.4 对于随机变量序列｛Xk；k≥1｝，如果对每个n和所有的x1，…，xn，都存在某一独立于n的正常数M，使得

成立，则称｛Xk；k≥1｝是广义下负相依（ELND）序列；如果对每个n和所有的x1，…，xn，都存在某一独立于n的正常数M，使得

成立，则称｛Xk；k≥1｝是广义上负相依（EUND）序列；如果对每个n和所有的x1，…，xn，都存在某一独立于n的正常数M，使得（1.5）式和（1.6）式同时成立，则称｛Xk；k≥1｝是广义负相依（END）序列。

如果（1.5）式和（1.6）式中的M=1，那么｛Xk；k≥1｝就是负相依（ND）序列；如果（1.5）式和（1.6）式中的不等号方向相反且M=1，那么｛Xk；k≥1｝就是正相依（PD）序列。显然，END序列包含了ND序列。对于某些PD序列，也可以找到某一正常数M使得（1.5）式和（1.6）式成立。

和Clayton copula函数：

当序列｛Xk；k≥1｝满足上述两类copula函数时，｛Xk；k≥1｝就是END序列。由于copula函数包含了很多相依结构，因此我们可以说Liu（2009）所提出的END相依结构是一类较为广泛的相依结构。

另一类相依结构常被称为拟渐近独立，是由Chen和Yuen（2009）所提出的。

定义1.5 两个非负随机变量X1和X2（分布函数分别为F1和F2）是拟渐近独立（QAI）的，如果

如果X1和X2同分布，那么就说它们是渐近独立。如果随机变量序列｛Xk，k≥1｝中的任意两个随机变量都是QAI的，则称｛Xk；k≥1｝是两两AQI（p QAI）序列。

基本符号及其变量的相依性

相关推荐