中文名 红尾伯劳拉丁名 Lanius cristatus英文名 Brown Shrike分类地位 雀形目伯劳科体长 18～20cm体重 26～35g野外识别特征 小型鸟类，和牛头伯劳相似，但红尾伯劳尾上覆羽红棕色，尾羽棕褐色，飞羽上无明显白斑。雏鸟晚成，经双亲共同喂养约16天离巢，离巢后仍随亲鸟在巢区活动一段时间学习捕食。分布与居留分布于亚洲东部。在我国广泛分布于多地，较为常见，在东北、华北等地繁殖，在繁殖地以南越冬。......
2023-11-03
重尾分布及其子族的研究
【摘要】：在风险理论中，索赔额分布可分为两大类：一类是轻尾分布，另一类是重尾分布。满足（1.4）式的F构成了整个重尾分布族，一般将重尾分布全体记作K。对重尾分布族的研究历来已久，由于其在应用概率领域，特别是分枝过程、排队论及风险理论等领域的广泛应用，人们对其的研究也越来越热。由于重尾分布族过于宽泛，考虑到保险等领域的实际需要，引入一些重尾分布子族。图1-2清楚地给出了各重尾分布子族之间的关系。
在风险理论中，索赔额分布可分为两大类：一类是轻尾分布，另一类是重尾分布。由于重尾分布已经被越来越多的学者认为是非寿险中个体索赔额的标准分布，首先介绍几类重要的重尾分布族以及它们的基本性质。
设随机变量X的分布函数为F（x）=P（X≤x），-∞＜x＜∞，其尾分布函数为
。我们约定对一切实数x，均有¯F（x）＞0。
定义1.2 如果随机变量X（其分布函数为F（x））不存在指数阶矩，即对任意的s＞0，若
则称随机变量X或分布函数F是重尾的；如果存在某个s＞0使得EesX有限，则称随机变量X或分布函数F是轻尾的。
满足（1.4）式的F构成了整个重尾分布族，一般将重尾分布全体记作K。根据定义1.2，如果随机变量X的期望不存在，那其自然是重尾的，因此一般考虑期望存在的情况。对重尾分布族的研究历来已久，由于其在应用概率领域，特别是分枝过程、排队论及风险理论等领域的广泛应用，人们对其的研究也越来越热。
由于重尾分布族过于宽泛，考虑到保险等领域的实际需要，引入一些重尾分布子族。如无特殊说明，均假设随机变量非负（即考虑支撑在［0，∞）上的分布）。下面就介绍一些重要的重尾分布子族，它们在后续章节中经常会被用到。
（1）
族：对任意的y，有
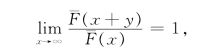
则称分布函数F属于长尾分布族，记作
。
（2）D族：对任意的0＜y＜1（或等价地y=1/2），有
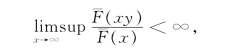
则称分布函数F属于控制变尾分布族，记作F∈D。
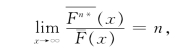
（3）S族：对任意的n≥2（或等价地n=2），有
=1-Fn*（x），Fn*（x）表示F的n重卷积，则称分布函数F属于次指数分布族，记作F∈S。
其中
（4）C族：如果
则称分布函数F属于一致变尾分布族，记作F∈C。
（5）ERV族：如果存在0≤α≤β＜∞，对任意的y＞1，有
则称分布函数F是广义正则变尾分布，记作F∈ERV（-α，-β）。广义正则变尾族ERV是所有的ERV（-α，-β）（0≤α≤β＜∞）的并集。
（6）R族：如果存在α≥0使得对所有的y＞0，有
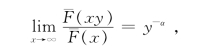
则称分布函数F是正则变尾分布，记作F∈R-α；R-α族包含了很多常用的分布，比如Pareto分布，Burr分布和t分布等。正则变尾族R是所有的R-α（0≤α＜∞）的并集。
对于上述提到的重尾分布子族，有如下的包含关系：
(1)R⊂ERV⊂C⊂
∩D⊂S⊂
⊂K；
(2)D⊄S，S⊄D。
关于这些包含关系的证明可以参考Embrechts等（1997）以及Cai和Tang（2004）。Cline和Sa morodnitsky（1994）构造了一些例子来说明C族严格包含ERV族且严格包含于D族；Embrechts等（1997）给出了Peter-Paul分布并说明它属于D族但不属于
族。图1-2清楚地给出了各重尾分布子族之间的关系。
图1-2 重尾子族关系表
有关若干重尾时依风险模型的渐近性质的文章
- 详细阅读
-
傈僳族名称及现代分布详细阅读
傈僳族是云南藏缅语系人群之一。汉人称之为傈僳，其自称为Lesuo。故此族之名称，自称或他族称之均为傈僳。至于“傈僳”一词之原来意义为何，询其本族人则已不知。吾以之询诸傈僳人，称并无此解。作者所调查的是黑傈僳。但是傈僳分布的中心区域的大部分，作者幸喜都得机会亲自涉足到。此傈僳族现代分布之概况。《皇清职贡图》谓楚庄蹻开滇时已有此种，是则当时必有傈僳之名称，但不知根据何书，兹暂置疑。......
2023-09-21
-
东北民歌文化研究：鄂伦春族及其分布详细阅读
鄂伦春族主要分布在内蒙古自治区东北部的鄂伦春自治旗、扎兰屯市、莫力达瓦旗、阿荣旗，黑龙江省的塔河、呼玛、逊克、嘉荫县和黑河市。清初文献曾把鄂伦春人称为“树中人”。从1690年十月始，“鄂伦春”才作为统一的族称固定下来。“鄂伦春”是民族自称，即“使用驯鹿的人们”。“奥伦”就是一种高脚的仓库，也是鄂伦春族特有的建筑。没有本民族文字，一般通用汉语，也有部分鄂伦春族用蒙古文。......
2023-11-16
-
红腹红尾鸲：特征、分布及习性详细阅读
中文名 红腹红尾鸲拉丁名 Phoenicurus erythrogastrus英文名 White-winged Redstart分类地位 雀形目鸫科体长 16～19cm体重 22～31g野外识别特征 小型鸟类，比其他红尾鸲体形偏大。雌鸟上体灰褐色，下体淡棕灰色，具不明显的白眼圈，腰至尾羽棕色。除繁殖期外单独或小群活动，栖息在石滩、灌木或地面上，尾部不住上下摆动。主食甲虫等昆虫，兼食蠕虫等其他小型无脊椎动物和少量植物种实。窝卵数3～5枚，卵白色具红棕色斑。分布与居留分布于中亚至东亚等地。......
2023-11-03
-
路由重分布的必要性及实施方法详细阅读
当多种路由选择协议“被拼凑”在一起时，使用重分配是很有必要的，而且重分配也是一个严谨网络设计的一部分。这种差异性使得向单一路由选择协议的迁移成为一项复杂的任务。简单来说，比如RouterA和RouterB配两个不同的动态路由协议，它们之间是没有LSA的，要想在Router上有对方的LSA就要做重分布。重发布只能在针对同一种第三层协议的路由选择进程之间进行，也就是说，OSPF，RIP，IGRP等之间可以重发布，因为它们都属于TCP/IP协议栈的协议。......
2023-11-19
-
蓝额红尾鸲：外貌、分布和特点详细阅读
中文名 蓝额红尾鸲拉丁名 Phoenicurus frontalis英文名 Blue-fronted Redstart分类地位 雀形目鸫科体长 14～16cm体重 14～25g野外识别特征 小型鸟类。雄鸟头颈、背和胸深灰蓝色，额和短眉纹鲜蓝色，翼暗褐色，其余体羽棕橙色，尾羽具黑色端斑，中央尾羽黑色。......
2023-11-03
-
路由重分布配置实现技巧详细阅读
重分布的命令格式如下：Router# redistribute protocol [protocol-id] { level-1 |level-2 | level-1-2 } {metric metric-value} {metric-type type-value} {match } {tag Tag-value} {route-map map-tag} {weight weight } {subnets}使用distance命令改变可信路由 ：distance weight [address mask [access-list-number | name] ] [ip]使用default-metric命令修改缺省度量值 ：default-metric number使用distribute-list命令过滤被重分布的路由 ：格式1：distribute-list {access-list-number | name} in [type number]格式2：distribute-list {access-list-number | name} out [interface-name |routing - process | autonomous-system-number]......
2023-11-19
-
倭瓜燕儿-鸟类图鉴：北红尾鸲的分布与特征详细阅读
中文名 北红尾鸲拉丁名 Phoenicurus auroreus英文名 Daurian Redstart分类地位 雀形目鸫科体长 13～15cm体重 13～22g野外识别特征 小型鸟类。雌鸟上体灰褐色，下体淡黄褐色，腰和尾棕橙色，褐色的翼上具白色翼斑。窝卵数通常6～7枚，雌鸟孵卵，雄鸟警戒，孵化期约13天。雏鸟晚成，经双亲喂养约14天后即可离巢。分布与居留分布于亚洲东部。在我国多地均有分布，较为常见，大多在长江以北地区繁殖、长江以南越冬，也有部分留鸟。......
2023-11-03
相关推荐