类似地，我们对副索赔及其相应的延后时间也给出一定的相依结构假设。在本节中我们将考虑带副索赔的时依风险模型中的有限时和无限时破产概率的渐近估计。对于p QAI索赔额序列，在其共同分布属于ERV族以及索赔额与索赔发生时间间隔相互独立的条件下，Li对模型的最终破产概率给出了如下的渐近估计。同时，我们也打算将定理2.3从ERV族推广至更大的控制变尾族，并给出有限时和无限时破产概率的渐近估计。......
2023-07-06
精算学中风险模型对破产概率的估算与控制
【摘要】：在精算科学中，精算学家通常会根据保险业务的历史数据所呈现的特征提出不同的风险模型，然后对风险模型的破产概率进行估算，并利用估计值的大小对整体风险进行度量以达到控制风险的目的。因此，我们给出有限时破产概率和无限时破产概率的定义。
从盈余的角度看，由于保险公司收取保费，有连续不断的保费进账，同时也不断地会有索赔需要支付，形成账面上的跳跃现象，因此盈余过程也是一个跳跃性的变化过程，直观上如图1-1所示。
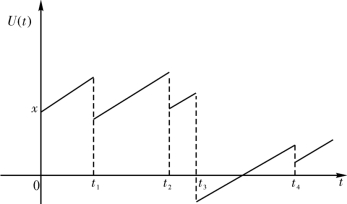
图1-1 盈余过程
在两次索赔发生的时刻之间（又称索赔发生时间间隔），盈余随着时间的变化而线性增加，增长的速度即是保费收入率（谢志刚和韩天雄（2000））。当发生索赔时，盈余跳跃性地减少与索赔相同的量。从图1-1可以看出，如果某一时刻发生了一次大额索赔（或发生了多个索赔），保险公司的盈余有可能为负值，这时可以形象并有点夸张地说“破产”这一事件发生了。但这并不是说保险公司将要倒闭，只是说保险公司可能会出现暂时的财务危机或者某一险种的经营状况不好，需要及时追加资金调整收支使保险公司继续经营或者改变该险种的经营策略等。因此，在保险实务中，破产概率（指在某段时间内保险业务的盈余出现负值这一随机事件发生的概率）已成为衡量保险公司（或某一险种）运营稳健性的一个重要指标，其为保费厘定、准备金的提留以及再保险计划的制定提供了直接的参考。在精算科学中，精算学家通常会根据保险业务的历史数据所呈现的特征提出不同的风险模型，然后对风险模型的破产概率进行估算，并利用估计值的大小对整体风险进行度量以达到控制风险的目的。因此，我们给出有限时破产概率和无限时破产概率的定义。
定义1.1 有限时破产概率：对某个固定的T≥0，在［0，T］内破产的概率
无限时破产概率（最终破产概率）：
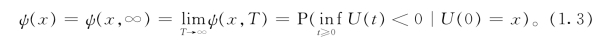
有关若干重尾时依风险模型的渐近性质的文章
- 详细阅读
-
带随机投资收益的重尾时依更新风险模型破产概率详细阅读
不失一般性，我们假设在0时刻其值为1，因此，到时刻t（≥0），保险公司的盈余过程可表示为：Tang等在F∈R以及｛L；t≥0｝与｛Xk；k≥1｝，｛θk；k≥1｝相互独立的条件下，建立了模型（2.1）的破产概率的渐近估计。在索赔额｛Xk；k≥1｝与索赔发生时间间隔｛θk；k≥1｝具有一定相依结构的条件下，给出本节的主要结论。......
2023-07-06
-
带投资和副索赔的二维重尾时依更新风险模型的破详细阅读
显然，副索赔发生在其主索赔之后，且延后的时间是随机的。因此，两保险公司具有随机投资收益的盈余过程分别为由此定义两类有限时破产概率由于在现实中索赔额与索赔发生的时间间隔之间往往是存在着一定的联系，因此在本节中对主索赔和副索赔仍旧采用假设B和假设C。......
2023-07-06
-
带随机投资收益的二维重尾时依更新风险模型破产详细阅读
本节考虑一类特殊的二维风险模型，其中两家保险公司共同承保标的（联保），并按δ1和δ2的比例承担索赔。为简单起见，假设两家保险公司只共同经营一种保险业务，且每个保险公司都有自己的投资策略，即每个保险公司的随机投资收益可能不同。这就意味着文中的随机投资收益R1和R2事实上也都是无风险投资与风险投资的组合。表3-1和3-2展示了在不同初始资金和分保比例情况下的数值模拟结果。至此，引理3.3证毕。......
2023-07-06
-
投资估算编制对项目决策和工程造价控制的影响详细阅读
4）项目决策的深度影响投资估算的精度，也影响工程造价的控制效果。2）项目投产后生产经营费用比较。应绘制主要的工艺流程图，编制主要物料平衡表，主要材料、辅助材料以及水、电、气等的消耗量等图表。5）选择的设备应符合政府部门或专门机构发布的技术标准要求。考点2 投资估算的概念及其编制内容一、投资估算的概念及作用概念 投资估算是指在项目投资决策过程中，依据现有的资料和特定的方法，对建设项目的......
2023-08-18
-
企业破产风险与防范的分析介绍详细阅读
企业破产，是指企业法人因严重亏损，无力清偿到期债务，依法清理其债务的法律制度。③只要满足上述情形之一的，即可被认定为出现了破产原因。若不明晰企业破产原因，可能会导致浪费司法资源、延缓企业破产进度等结果。破产重整程序详见《企业破产法》第八章。清算人作为申请人，仅可向法院申请破产清算。......
2023-08-02
-
混业经营对风险控制的不利因素详细阅读
逆周期的宏观审慎管理制度对于银行的调控尤其有好处，避免了经济的大幅波动从而有效地防范了金融危机。所以，构建逆周期的宏观审慎管理制度框架的优势在于着眼于整个金融体系，重点关注金融机构之间的相互作用及金融机构面临的共同风险，有利于加强整个金融体系的稳定性，防范系统性金融风险。......
2023-07-19
-
破产制度对破产启动程序的影响分析详细阅读
在征得申请执行人之一或者被执行人的同意后，将符合破产条件且执行不能的案件向有管辖权的法院移送破产。但需要明确的是在转入破产程序之前是需以执行申请人之一或被执行人同意为条件的，没有当事人的同意，执行转破产程序则无法启动。......
2023-08-07
相关推荐