图2.3朗格朗日网格与欧拉网格对比欧拉算法也有其不足,体现为单个循环计算时间长、材料边界不清晰、网格区域过大、冲击波耗散大、强度模拟不精确等。图2.4欧拉-拉格朗日耦合算法模型4.SPH算法SPH算法,即光滑粒子流体动力学数值算法,为固体材料大变形,尤其是存在破坏、断裂等极大变形的非线性动力学行为数值模拟提供了新的手段。......
2023-06-18
数学模型既然这么有用,我们如何获取它呢?此时各种各样我们曾经学过却很少使用的物理公式终于要发挥作用了。
我们知道数学模型就是用数学的表达方式把无人机在物理定律下运动的情况描述出来,有哪些物理定律可以使用呢?
无人机系统运动受力和力矩的作用,在分析系统情况时常使用拉格朗日方程与牛顿-欧拉方程。
1)拉格朗日方程

图6.11 “一个人的贡献和他的自负严格地成反比,这似乎是品行上的一个公理”,数学家的身份,“严格地成反比”的描述都让这句话显得意味深长(图片来源:维基百科)
拉格朗日方程可能是机器人系统数学建模中使用最多的公式了,它不仅可以应用在无人机系统的学习和研究中,还可以应用在机械臂、双足机器人、四足机器人、地面轮式机器人、地面履带式机器人等领域。因此掌握拉格朗日方程可以让读者在众多应用领域中受益。
拉格朗日方程可以看作是对牛顿第二定律的一种“引申”,它引入了广义坐标,借助达朗贝尔原理推出了实质上和牛顿第二定律等价的结论。这也许能够给有项目压力或者专利指标的读者一个很好的启发:同样的一个事物,仅仅换一个思考角度就可以带来一些不同的收获。这并非投机取巧的行为。拉格朗日方程为什么会被如此多的工程师使用呢?原因在于应用拉格朗日方程分析系统时可以得到最少的动力学方程,同时在分析过程中也无须对具体的加速度运动有过多投入。虽然拉格朗日方程在本质上与牛顿第二定律区别不大,但是这样一个新的角度却给问题的解决提供了很多便利(请思考问题:在我们的生活中是不是有类似的情形呢?换一个角度能带来哪些不同?)。
在进入拉格朗日公式前,先要引入一个称为拉格朗日函数的小东西:
L=T-V, (6.17)
这个算子代表了整个系统中最为重要的部分:能量。其中T表示系统动能(Kinetic Energy),V表示系统势能(Potential Energy)。当有了这个算子后,我们就可以直接观察拉格朗日方程:

其中qi为广义坐标,Γi为广义力。本节中不会介绍拉格朗日方程的推导,但这并不会妨碍我们理解拉格朗日的本质,如果读者对推导过程很有兴趣可以在附录中查找需要的参考文献或者任何一本分析力学书籍。拉格朗日方程与牛顿-欧拉方程都是将牛顿第二定律从惯性坐标系推广到更加“广义”的运动体系中,虽然实现的途径略有不同。
前文已经介绍拉格朗日引入了“广义坐标”,什么是广义坐标呢?广义坐标是与“自由度”和约束相关联的,前文给出了自由度的定义与理解方法,在这里可以更深一层展开。
很容易理解无人机沿机身的三个坐标轴进行直线运动,我们可以针对它的直线运动建立多个惯性坐标系,我们也很清楚无人机可以围绕着机体坐标系的三个轴线进行旋转运动,习惯上称之为俯仰旋转、横滚旋转、偏航旋转。无人机的直线运动可以放入我们熟悉的R3空间中,三个相互垂直的单位向量构成了一个显而易见的坐标系,帮助我们描述无人机在R3空间中的线性位置,并且通过位置求导获取无人机直线运动速度信息。自然而然的,我们会把这样的思考方式应用在旋转运动中,但一个问题紧随而来:旋转运动在这样的坐标系中怎么表示呢?
我们能够将无人机放在惯性坐标系中并且轻松理解对应的运动情况,是因为我们很习惯将无人机看作质点。质点是非常常见的物理学概念,大家在学习高中物理时会常常遇到这两个字,回想一下很多高中物理考卷中对应力学题目的开篇通常是“某质点……”。显然把研究对象抽象为质点对于惯性坐标系下的运动描述是简单、直观的,一旦产生旋转运动,质点的描述功能就显得非常无力了,一个质点怎么会发生旋转呢?此时我们要把无人机看作刚体,即在运动和受外力作用后,形状与大小不变,内部各点的相对位置不变的物体。刚体在空间的位置,必须根据刚体中任一点的空间位置和刚体绕该点转动时的位置来确定,这正是无人机六个自由度:[X,Y,Z,ϕ,θ,ψ]的来源。因此当引入了刚体后就多出了三个独立坐标来描述旋转运动,与此同时,拉格朗日引入了“广义坐标”,使得约束可以也成为自由度计算的一部分。
刚体的概念把质点的运动描述从三维度空间扩展到了六自由度系统,在这个系统里无人机有六个相互独立的参数来描述直线运动和旋转运动。通过广义坐标的概念,将约束条件带入到系统运动中,并在此基础上应用最为基本的,由牛顿第二定律所揭示的力与运动之间的关系。
拉格朗日方程有多种形式,式(6.18)可以称为主动力为有势力的拉格朗日方程。通过前文的介绍,我们已经理解了无人机旋转运动下的自由度、无人机系统运动描述的广义坐标来源等,现在我们终于可以定性地考察一下(6.18)中拉格朗日方程形式的直观物理意义。
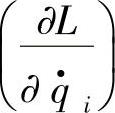 为能量差对速度的偏微分,读者可以比照较为熟悉的惯性系统来理解,在惯性系统中,动能对速度的偏微分是什么呢?
为能量差对速度的偏微分,读者可以比照较为熟悉的惯性系统来理解,在惯性系统中,动能对速度的偏微分是什么呢?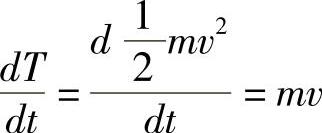 ,最后的结果就是动量。把这样的关系带入到广义坐标系中就得到了广义动量。广义动量可以是质点的线动量,也可以对应于无人机系统的刚体旋转动量。而
,最后的结果就是动量。把这样的关系带入到广义坐标系中就得到了广义动量。广义动量可以是质点的线动量,也可以对应于无人机系统的刚体旋转动量。而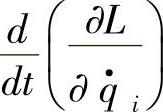 则是广义动量对时间的导数,读者可以对比一般动量的情形:
则是广义动量对时间的导数,读者可以对比一般动量的情形: ,由此可将广义动量对时间的导数理解为一个广义力。方程中的另外一个量
,由此可将广义动量对时间的导数理解为一个广义力。方程中的另外一个量 是能量差对位置求偏微分,读者比较熟悉的是重力势能对位置的偏微分:
是能量差对位置求偏微分,读者比较熟悉的是重力势能对位置的偏微分: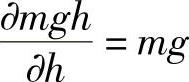 ,因此拉格朗日方程中,该量也是一个广义力。(6.18)式等号右边的定义也是广义力,因此整个方程等号的含义可以理解为:系统的广义惯性力与广义主动力相等。
,因此拉格朗日方程中,该量也是一个广义力。(6.18)式等号右边的定义也是广义力,因此整个方程等号的含义可以理解为:系统的广义惯性力与广义主动力相等。
把无人机系统的动能和势能带入到(6.18)中,可以得到无人机数学模型:
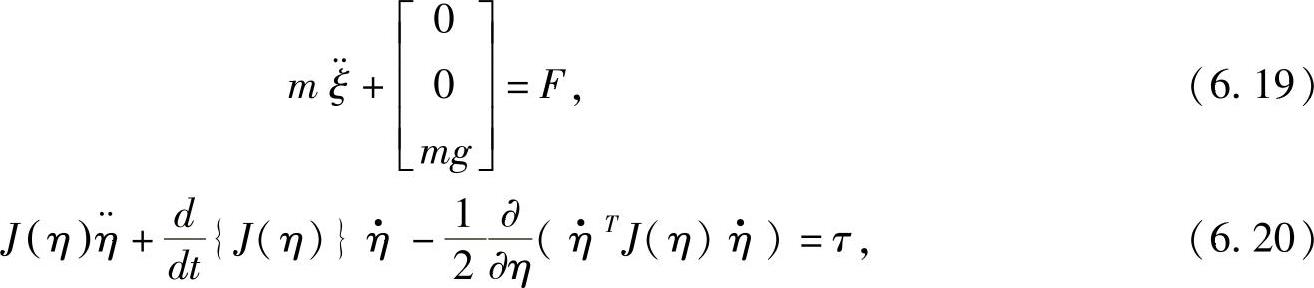
其中 =[X,Y,Z]T∈R3为无人机系统的外环状态,η=[ϕ,θ,ψ]T∈R3为无人机系统的内环状态,J(η)为广义惯量矩阵,F=[Fx,Fy,Fz]T为无人机在三个方向上受到的合外力向量。无人机外环姿态模型通过牛顿第二定律是比较容易获取的,内环数学模型在通过一系列简化运算后可以得到如下形式:
=[X,Y,Z]T∈R3为无人机系统的外环状态,η=[ϕ,θ,ψ]T∈R3为无人机系统的内环状态,J(η)为广义惯量矩阵,F=[Fx,Fy,Fz]T为无人机在三个方向上受到的合外力向量。无人机外环姿态模型通过牛顿第二定律是比较容易获取的,内环数学模型在通过一系列简化运算后可以得到如下形式:
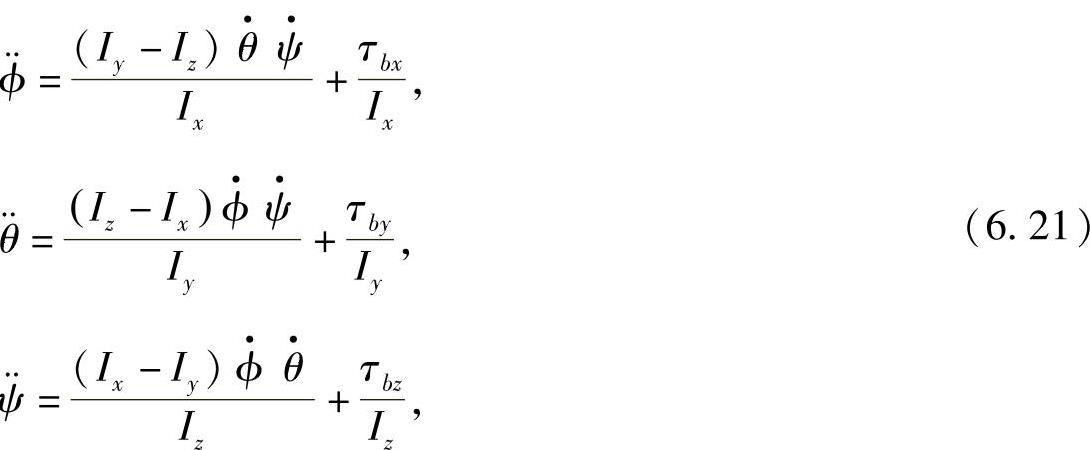
其中τbx,τby,τbz分别为无人机在机体坐标系中绕X,Y,Z轴所受的力矩。以四旋翼无人机为例,力矩分为两个部分,第一部分由螺旋桨的升力产生,具体升力公式可参考(5.2)、(5.3)式,计算力矩只要在乘以对应四旋翼操作方式:十字形、X形,旋翼中心到轴线的距离即可。第二部分来自于旋翼旋转时的陀螺效应,可用下面的公式计算:
τx=Jrωy(Ω1-Ω2),
τy=-Jrωx(Ω1-Ω2), (6.22)
其中Ω1为无人机顺时针方向旋转的螺旋桨转速和,Ω2为无人机逆时针方向旋转的螺旋桨转速和。
通过拉格朗日方程推导无人机数学模型既可以加深使用者对无人机系统运动的理解和思考,也可以将动力学方程的数目减到最小。由于本节是在无约束情况下进行的计算,因此拉格朗日方程的优势并没有完全展现出来,但在真实的无人机系统中,任务可能会提出对无人机系统的实际约束,在这类应用中拉格朗日方程可以发挥出更多的功效。
2)牛顿-欧拉方程
拉格朗日方程在使用中存在两个问题,一方面在采用拉格朗日方程获取无人机数学模型时采用了很多化简步骤才能得到(6.21)这样的简洁形式。另一方面推导过程和理解对于非物理专业的读者而言有着比较大的难度,虽然在前面的内容中花了比较大的篇幅来介绍拉格朗日方程,以便读者建立更为直观的理解,但是不得不承认拉格朗日方程与我们的直观感触还是相差较远,它的证明过程比较抽象,引入了虚位移原理和广义坐标等概念,在实际应用中对数学运算和抽象理解能力要求较高。因此有没有一种相对而言更为直观的无人机数学模型推导方式呢?既然引入了刚体这样方便的概念,能否运用更加熟悉的传统力学方式来进行推导呢?这就引出了无人机数学模型推导的另外一种方法:矢量动力学,又称为牛顿-欧拉动力学。下面给出无人机系统所对应的牛顿-欧拉方程矩阵形式:

其中I为一个三阶矩阵,对于多旋翼无人机,可以直接简化为对角阵,对角元素分别为无人机在三个方向上的转动惯量;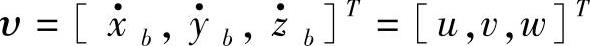 为无人机沿机体坐标系三个方向上的线性速度向量;ω=[p,q,r]T为无人机角速度向量;fb,τb分别为无人机在机体坐标系下受到的合外力、合外力矩向量。(6.23)可以直接看作牛顿第二定律在旋转刚体中的应用。在这里我们要特别提到叉乘运算,这种运算方式只用于三维线性空间,具体计算方法:设三个向量
为无人机沿机体坐标系三个方向上的线性速度向量;ω=[p,q,r]T为无人机角速度向量;fb,τb分别为无人机在机体坐标系下受到的合外力、合外力矩向量。(6.23)可以直接看作牛顿第二定律在旋转刚体中的应用。在这里我们要特别提到叉乘运算,这种运算方式只用于三维线性空间,具体计算方法:设三个向量 ,
, ,
, ,假设
,假设 ,有:
,有:

其中矩阵A,B分别为由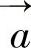 ,
,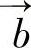 对应元素构成的反对称阵。
对应元素构成的反对称阵。 的方向符合右手定则,垂直于
的方向符合右手定则,垂直于 ,
, 向量所确定的平面。
向量所确定的平面。
欧拉方程与拉格朗日方程在结果上是完全一样的,习惯上采用拉格朗日方程获取无人机内环动态时进行小角度化简,即认为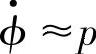 ,
,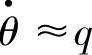 ,
, ,而它们之间的实际关系应为:
,而它们之间的实际关系应为:
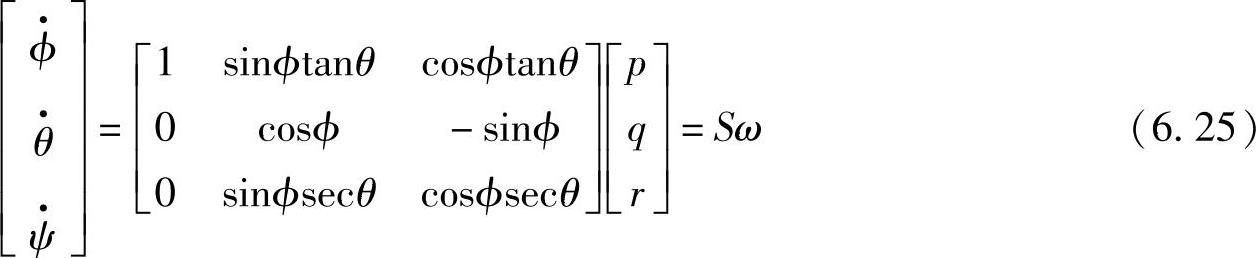
当下的很多无人机产品或飞行控制器都提供限速功能,比如将无人机的飞行线速度限制在10m/s以内,或者垂直速度限制在5m/s等,此时无人机沿三轴线运动,姿态角都比较小,因此可以认为S矩阵约等于单位阵。
无论是使用拉格朗日方程还是牛顿-欧拉方程,我们都可以得到关于无人机系统12个状态的完整数学表达式,在这里结合式(6.10),(6.19),(6.21)给出:
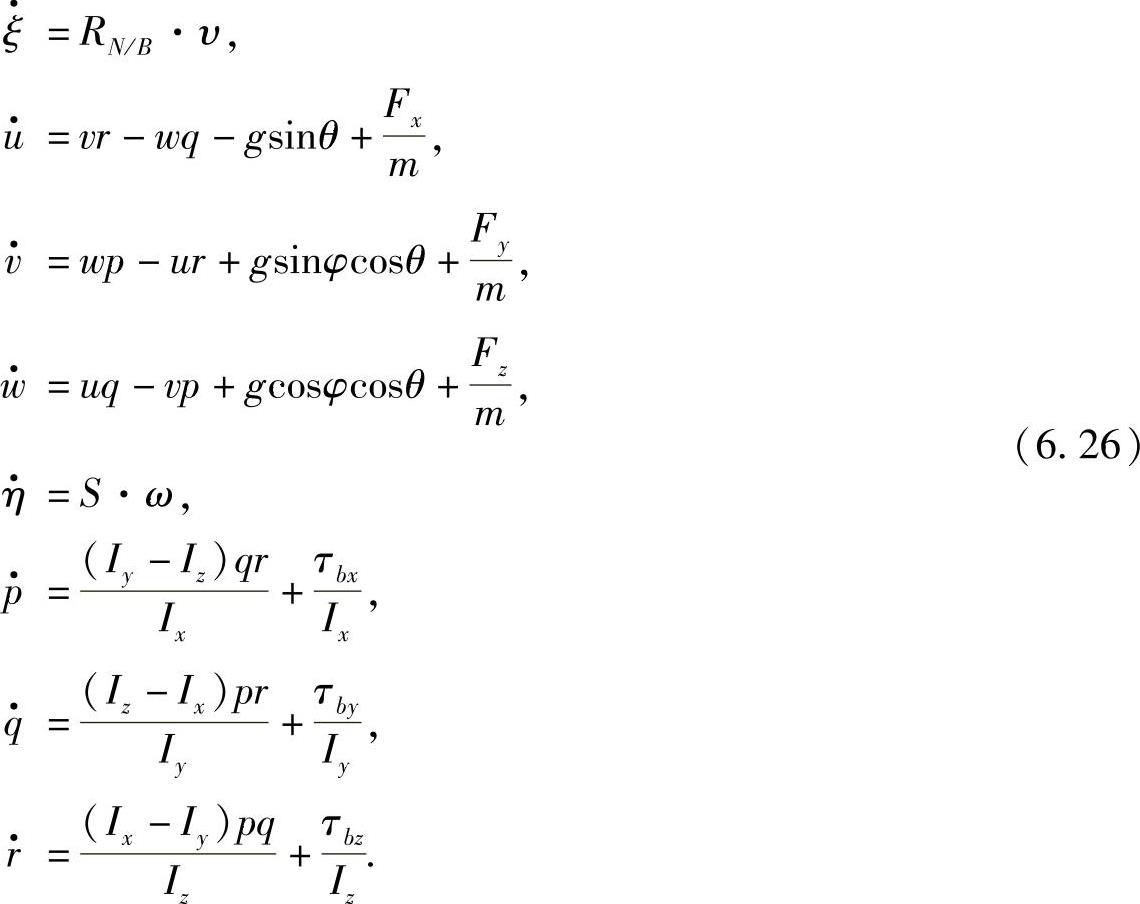
有关城堡里学无人机:原理、系统与实现的文章

图2.3朗格朗日网格与欧拉网格对比欧拉算法也有其不足,体现为单个循环计算时间长、材料边界不清晰、网格区域过大、冲击波耗散大、强度模拟不精确等。图2.4欧拉-拉格朗日耦合算法模型4.SPH算法SPH算法,即光滑粒子流体动力学数值算法,为固体材料大变形,尤其是存在破坏、断裂等极大变形的非线性动力学行为数值模拟提供了新的手段。......
2023-06-18

上面所讨论的极值问题,对于函数的自变量,除了限制在函数的定义域内以外,并无其他条件,所以有时候称为无条件极值.但在实际问题中,有时会遇到对函数的自变量还有附加条件的极值问题.例如,求表面积为a2而体积为最大的长方体的体积问题.设长方体的三条棱的长为x,y,z,则体积V=xyz.又因假定表面积为a2,所以自变量x,y,z还必须满足附加条件2(xy+yz+xz)=a2.像这种对自变量有附加条件的极值称......
2023-10-19

合唱教学在高校艺术教育活动中占有极其重要的地位,教师在组织合唱教学过程中,只有在融洽的气氛中学习、训练,才能取得良好的教学效果。目前我国合唱指挥教学存在着诸多问题,可采用综合学科的复合教学、多媒体与网络技术教学及灵活多样的教学手段,实现合唱指挥教学变革。因此,在合唱教学中应该采用灵活多变的教学手段。微格教学实质上是一种协作式教学,对有效地开展合唱教学能起到积极作用。......
2023-10-18

平面一般力系平衡的充分与必要条件是:力系的主矢和主矩同时为零。上式称为平面一般力系的平衡方程,平面一般的平衡方程有三个,可求解最多三个未知量。显然各力作用线在同一平面内且任意分布,属于平面一般力系。列平衡方程要根据物体所受的力系类型列出。比如,平面任意力系只能列出三个独立的平衡方程,平面汇交力系或平面平行力系只能列两个;平面力偶系只能列一个;对于由n 个物体组成的系统,可列出3n 个。......
2023-06-19

在导师的理论指导下,对一小组学生进行10分钟左右的“微格教学”,并当场将实况用摄像机摄录下来。爱伦和伊芙把微格教学定义为:“一个有控制的实习系统,它使师范生有可能集中解决某一特定的教学行为,或在控制的条件下进行学习。”......
2023-10-31

在我国,无人机巡检的工作同样在有条不紊地进行中。在塔架的运维工作中,无人机能够长期记录塔架状态,通过正射影像投影法,可判断形变量及变形趋势,为整改工作提供依据。桥梁检查常规桥梁检查的工作都是由工程公司的检查人员亲自完成。选择无人机参与测试,就是希望节省作业时间,保证正常交通,甚至探测一些肉眼所无法观测到的潜在问题。类似铁路巡检,用无人机检查桥梁同样也处于初期探索和试错的阶段。......
2023-07-23

变系数的线性微分方程,一般说来都是不容易求解的.但是有些特殊的变系数线性微分方程,则可以通过变量代换化为常系数线性微分方程,因而容易求解,欧拉方程就是其中的一种.形如的方程(其中,p1,p2…pn为常数),叫做欧拉方程.作变换x=et或t=lnx,将自变量x换成t,有如果采用记号D表示对t求导的运算,那么上述计算结果可以写成一般地,有xky=D(D-1)…......
2023-11-22
相关推荐