线上实例展示：三角函数的应用举例

2023-07-03 理论教育版权反馈

【摘要】：4．2018年4月12日上午，中央军委在南海海域隆重举行海上阅兵，展示人民海军崭新面貌，激发强国强军坚定信念．如图，一艘补给舰位于一艘综合登陆舰P的北偏东60°方向，与综合登陆舰P的距离为40海里的A处，补给舰沿正南方向航行一段时间后，到达位于综合登陆舰Ｐ的南偏东３０°方向上的Ｂ处，则此时补给舰所在位置Ｂ处与综合登陆舰Ｐ之间的距离为（）．（第7题）（2）小船从点P处沿射线AP的方向进行沿途考察，

4．2018年4月12日上午，中央军委在南海海域隆重举行海上阅兵，展示人民海军崭新面貌，激发强国强军坚定信念．如图，一艘补给舰位于一艘综合登陆舰P的北偏东60°方向，与综合登陆舰P的距离为40海里的A处，补给舰沿正南方向航行一段时间后，到达位于综合登陆舰Ｐ的南偏东３０°方向上的Ｂ处，则此时补给舰所在位置Ｂ处与综合登陆舰Ｐ之间的距离为（）．

（第7题）

（2）小船从点P处沿射线AP的方向进行沿途考察，求观景台B到射线AP的最短距离．（结果保留根号）

8．如图，轮船在A处观测灯塔C位于北偏东70°方向上，轮船从A处以每小时30海里的速度沿南偏东50°方向匀速航行，1小时后到达码头B处，此时观测灯塔C位于北偏东25°方向上，求灯塔C与码头B之间的距离．（结果保留根号）

（第8题）

9．如图，为了测量小河AE的宽度，小明从河边的点A处出发沿着斜坡AB行走260m至坡顶B处，斜坡AB的坡度为i＝1∶2．4，在点B处测得小河对岸建筑物DE顶端点D的俯角∠CBD＝11°，已知建筑物DE的高度为37．5 m，则小河AE的宽度约为（）．（精确到1 m，参考数据：sin 11°≈0．19，cos 11°≈0．98，tan 11°≈0．20）

（第9题）

A．89m

B．73m

C．53m

D．43m

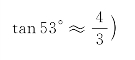
10．某数学社团开展实践性研究，在大明湖南门A测得历下亭C在北偏东37°方向，继续向北走105m后到达游船码头B，测得历下亭C在游船码头B的北偏东53°方向．那么南门A与历下亭C之间的距离约为（）．（参考数据： pagenumber_ebook=141,pagenumber_book=133

（第10题）

A．225m B．275m C．300m D．315m

11．为缓解交通压力，市郊某地正在修建地铁站，拟同步修建地下停车库．如图是停车库坡道入口的设计图，其中MN是水平线，MN∥AD，AD⊥DE，CF⊥AB，垂足分别为点D，F，坡道AB的坡度＝1∶3，AD＝9m，点C在DE上，CD＝0．5m，CD是限高标志牌的高度（标志牌上写有：限高________m）．如果进入该车库车辆的高度不能超过线段CF的长，则该停车库限高多少m？（结果精确到0．1m，参考数据：

（第11题）

线上实例展示：三角函数的应用举例

相关推荐