把一个平面图形绕着平面内某一点O旋转一个角度，叫做图形的_________，点O叫做________，转动的角叫做________．
旋转的性质：对应点到旋转中心的距离________．对应点与旋转中心所连线段的夹角等于_________．旋转前、后的图形________．
1．下列现象：①时针的转动；②摩天轮的转动；③地下水位逐年下降；④传送带上的机器人．其中属于旋转的是（ ）．
A．①② B．②③ C．①④ D．③④
2．一辆模型赛车，先前进1m，然后沿原地逆时针方向旋转，旋转角为α（0＜α＜90°），被称为一次操作，若五次操作后，发现赛车回到出发点，则旋转角α为（ ）．
A．108° B．120° C．72° D．36°
3．如图，小明坐在秋千上，秋千旋转了76°，小明的位置也从A点运动到了A′点，则∠OAA′的度数为（ ）．
A．28° B．52° C．74° D．76°
（第3题）
（第4题）
4．如图，将Rt△ABC绕直角顶点C按顺时针方向旋转90°后得到△A′B′C，连接AA′．若∠1＝25°，则∠B的度数为（ ）．
A．55° B．65° C．60° D．70°
5．如图，在Rt△ABC中，∠ACB＝90°，∠B＝35°．将△ABC绕点C逆时针旋转α得到△DCE，若DC∥AB，则旋转角α的度数为（ ）．
A．35° B．45° C．55° D．65°
（第5题）
（第6题）
6．如图，△ODC是由△OAB绕点O顺时针旋转30°后得到的图形，若点D恰好落在AB上，则∠ADO的度数为（ ）．
A．30° B．60° C．75° D．80°
7．如图所示，将图形①以点O为旋转中心，每次顺时针旋转90°，则第2019次旋转后的图形是________．（在下列各图中选填正确图形的序号即可）
（第7题）
8．如图，在△ABC中，∠ABC＝112°，将△ABC绕着点B顺时针旋转一定的角度后得到△DBE（点A与点D对应），当A，B，E三点在同一直线上时，∠DBC的度数为_________．
（第8题）
9．如图，在四边形ABCD中，∠ABC＝∠ADC＝45°，将△BCD绕点C顺时针旋转一定角度后，点B的对应点恰好与点A重合，得到△ACE．（1）请求出旋转角的度数；
（2）请判断AE与BD的位置关系，并说明理由；
（3）若AD＝2，CD＝3，试求出四边形ABCD的对角线BD的长．
（第9题）
10．在Rt△ABC中，∠ABC＝90°，∠BAC＝30°，将△ABC绕点A顺时针旋转一定的角度α得到△AED，点B，C的对应点分别是点E， D．
（1）如图1，当点E恰好在AC上时，求∠CDE的度数；
（2）如图2，若α＝60°时，F是AC的中点，求证：四边形BFDE是平行四边形．
（第10题）
11．如图，在△ABC中，以C为中心，将△ABC顺时针旋转35°得到△DEC，边ED，AC相交于点F，若∠A＝30°，则∠EFC的度数为（ ）．
（第11题）
A．60° B．65° C．72．5° D．115°
（第12题）
13．如图，已知正方形ABCD的边长为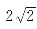
，点E是对角线AC上一点，连接DE，将线段DE绕点D顺时针旋转90°至DF的位置，连接AF，EF．
（1）求证：△ADF≌△CDE；
（2）当点E在什么位置时，△AEF的面积最大？并说明理由．
（第13题）
旋转命令可以改变选择图形和图形组合的方向。图3.55 旋转命令对话框旋转命令可以采用对话框，也可以采用鼠标完成：采用对话框完成旋转命令流程：1）选择命令Edit→Other→Rotate或者快捷键Shift+o；2）选择版图中的图形；3）鼠标在版图中单击参考点，在旋转命令对话框中填入旋转的角度或者选择Rotate/Sideways/Upside Down；4）单击Apply完成旋转操作。图3.56 逆时针旋转90°操作示意图图3.57 目标关于Y轴镜像与X轴镜像操作示意图......
2023-06-26
平面的旋转可以解决以下三个作图问题。因此，在平面内作一条投影面平行线进行旋转即可。这要改变平面对V面的倾角，因而应选择铅垂线为旋转轴。图3-63所示为将一般位置平面△ABC旋转成水平面的作图过程：首先把△ABC旋转成正垂面，然后再把正垂面旋转成水平面。......
2023-06-28
ROTATE命令可以将所选定的对象沿某一选定的基准点旋转一定的角度，默认删除源对象，也可以选择选项，保留源对象。执行ROTATE命令可采用以下三种方式：●工具栏 。将正六边形旋转30°，操作如下：命令：_rotateUCS当前的正角方向：ANGDIR=逆时针 ANGBA......
2023-06-21
1．下面四个车标图案中，既不是旋转对称图形又不是轴对称图形的是（ ）．2．等边三角形绕着它的中心O旋转，若旋转后的三角形能与自身重合，则旋转角最小是（ ）．A．360° B．240°C．120° D．60°3．国旗上的五角星需要旋转一定度数后才能与自身重合，这个度数为（ ）．A．36° B．60° C．45° D．72°4．在如图所示的网格中，每个小正方形的边长均为1，△ABC的三个顶点都是网格线......
2023-07-03
为了将平面旋转到有利于解题的特殊位置，关键是确定旋转轴的位置和选择适当的旋转角度。2）将投影面垂直面旋转成投影面平行面以正垂线为旋转轴，可将正垂面旋转为水平面，其H投影反映实形。如图4—20所示，△ABC为正垂面，绕通过B点的正垂轴旋转，使其变换为水平面△A1BC1，于是△a1bc1≌△ABC。图4—21一般面旋转为水平面......
2023-09-24
璀璨的星空令人无限神往,哥白尼曾说:“有什么东西能比天空更美好呢?要知道天空囊括了一切美好的东西．”左图是埃舍尔创作的《星空》,他对多面体和框架星体情有独钟,主体框架星体里住着两条变色龙,给宇宙星空增添了生气和趣意．知能概述图形有具体的,有抽象的;有平面的,有立体的．它既可以是艺术中的绘画和雕塑,也可以是科学上的表达或记录．立体图形与平面图形之间的联系体现在以下方面:立体图形的展开与折叠,从不同方......
2023-08-13
此时需要选择旋转的基点，因为图形将会围绕基点旋转。示例3-5 旋转图形思路·点拨本示例将以简单的旋转操作来向读者介绍如何精确地旋转图形。打开附带光盘目录下的“Start\Ch3\示例3-5.dwg”，图形如图3-48所示，下面将详细说明如何准确地以A为基点旋转矩形使其AB边与直角三角形的AC边重合。图3-48 旋转前的图形在命令行中输入“ROTATE”，执行命令，选中矩形为旋转对象，按〈Enter〉键确定，命令行中会出现如下提示信息。旋转完成后的图形如图3-51所示。......
2023-09-22
相关推荐