当m取何值时为二次函数？......
2025-09-29
二次函数与一元二次方程：22.7的相互关系
【摘要】：一般地，从二次函数的图象可以得到下列结论：（1）如果抛物线y＝ax2＋bx＋c与x轴有公共点，公共点的横坐标是x0，那么当x＝x0时，函数值是_________，因此，x＝x0就是一元二次方程_________________的根．（2）抛物线y＝ax2＋bx＋c与x轴的位置关系有三种：_________________，_________________，_________________；这对
一般地，从二次函数的图象可以得到下列结论：
（1）如果抛物线y＝ax2＋bx＋c与x轴有公共点，公共点的横坐标是x0，那么当x＝x0时，函数值是_________，因此，x＝x0就是一元二次方程_________________的根．
（2）抛物线y＝ax2＋bx＋c与x轴的位置关系有三种：_________________，_________________，_________________；这对应着一元二次方程ax2＋bx＋c＝0的根也有三种情况：_____________________，___________________，_____________________．
（第1题）
1．函数y＝ax2＋bx＋c的图象如图所示，关于x的一元二次方程ax2＋bx＋c－4＝0的根的情况是（ ）．
A．有两个相等的实数根
B．有两个不相等的实数根
C．没有实数根
D．有两个异号的实数根
2．下列关于抛物线y＝x2＋bx－2的说法中，正确的是（ ）．
A．抛物线的开口方向向下
B．抛物线与y轴交点的坐标为（0，2）
C．当b＞0时，抛物线的对称轴在y轴右侧
D．对于任意的实数b，抛物线与x轴总有两个公共点
3．已知抛物线y＝ax2＋bx＋c的部分图象如图所示，则当y＞0时，x的取值范围是（ ）．
（第3题）
A．x＜3
B．x＞－1
C．－1＜x＜3
D．x＜－1或x＞3
4．抛物线y＝－x2＋2x－2与坐标轴的交点个数为（ ）．
A．0 B．1 C．2 D．3(https://www.chuimin.cn)
5．已知二次函数y＝x2＋x＋m，当x取任意实数时，都有y＞0，则m的取值范围是（ ）．
6．如图，二次函数y＝ax2＋bx＋c的图象与y轴正半轴相交，其顶点坐标为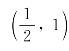
，下列结论：①abc＜0；②4ac＜b2；③a＋b＋c＜0；④方程ax2＋bx＋c－1＝0一定有两个相等的实数根．其中正确的有（ ）．
（第6题）
A．1个 B．2个 C．3个 D．4个
7．若抛物线y＝ax2－2ax－3与x轴交于两点，分别是（m，0），（n，0），则m＋n的值为_________．
8．有一个二次函数的图象，三名同学分别说了它的一些特点：
甲：与x轴只有一个交点；
乙：对称轴是直线x＝3；
丙：与y轴的交点到原点的距离为3．
满足上述全部特点的二次函数的解析式为__________________________________．
9．若抛物线y＝ax2＋bx－3的对称轴为直线x＝1，且该抛物线经过点（3，0）．
（1）求该抛物线对应的函数解析式．
（2）当－2≤x≤2时，则函数值y的取值范围为_________________．
（3）若方程ax2＋bx－3＝n有实数根，则n的取值范围为_________________．
10．已知抛物线的解析式是y＝x2－（k＋2）x＋2k－2．
（1）求证：此抛物线与x轴必有两个不同的交点；
（2）若抛物线与直线y＝x＋k2－1的一个交点在y轴上，求该抛物线的顶点坐标．
11．已知二次函数y＝（x－p）（x－q）＋2，若m，n是关于x方程（x－p）（x－q）＋2＝0的两个根，则实数m，n，p，q的大小关系可能是（ ）．
A．m＜p＜q＜n B．m＜p＜n＜q
C．p＜m＜n＜q D．p＜m＜q＜n
12．若抛物线的顶点坐标为（2，9），且它在x轴截得的线段长为6，则该抛物线的解析式为_________．
相关文章
- 详细阅读
-
一元二次方程的根与系数的关系及优化方案详细阅读
对于一元二次方程ax2＋bx＋c＝0（a≠0），当b2－4ac≥0时，设方程的两个实数根为x1，x2，那么x1＋x2＝________，x1x2＝________．1．设α，β是一元二次方程x2＋2x－1＝0的两个实数根，则αβ的值是（ ）．A．2 B．1 C．－2 D．－12．若方程3x2－4x－4＝0的两个实数根分别为x1，x2，则x1＋x2＝（ ）．3．下列一元二次方程中，两实数根的和为－4......
2025-09-29
-
微观分析:水泥固化硫酸污染土中水化产物与孔隙详细阅读
图3.7水泥固化硫酸污染土微观照片水泥土的电阻率主要来源于两部分，一部分是各种水化产物自身的电阻率，另一部分是水泥土孔隙水的电阻率，水化产物的电阻率值很大，所以水泥土的电阻率取决于孔隙水，孔隙结构越致密则导电性越差，电阻率越大，反之则电阻率越小。......
2025-09-29
-
厌氧生物处理中优势菌群的演替及相互关系详细阅读
在厌氧生物处理中，存在着种类繁多、关系非常复杂的微生物区系。厌氧生物处理过程实际上是这些微生物所进行的一系列生物化学的偶联反应，而产甲烷细菌则是厌氧生物链上的最后一个成员。以上第一种关系最为重要，在厌氧处理系统中，产酸细菌和产甲烷细菌相互依赖，互为对方创造良好的环境和条件，构成互生关系。同时，双方又互为制约，在厌氧生物处理系统中处于平衡状态。......
2025-09-29
-
调水工程课题及相互关系分析详细阅读
调水工程的规模越大，所涉及的学科就有可能越多。下面我们根据戈罗彪夫Г·Н·教授所划分的这些子课题，结合其他学者的研究成果，简要地介绍这些子课题的内容，并提出一些新的问题。图1-1调水工程各课题的结构示意图1.技术工艺主课题实现调水和保证其发挥作用的工程系统。该课题与经济效益问题密切相关。该课题是研究自然资源与大型调水工程之间的关系。......
2025-09-29
-
实际问题与一元二次方程的应用详细阅读
1．如图，在△ABC中，∠ABC＝90°，AB＝4cm，BC＝3cm，动点P，Q分别从点A，B同时开始移动（移动方向如图所示），点P的速度为cm／s，点Q的速度为1cm／s，点Q移动到点C后停止，点P也随之停止运动，若使△PBQ的面积为cm2，则点P运动的时间是（ ）．（第1题）A．2s B．3s C．4s D．5s2．一个数学兴趣小组的同学毕业时都将自己的照片向组内其他同学各送一张表示留念，共送......
2025-09-29
-
解决实际问题的一元二次方程详细阅读
6．某水果店进口一种高档水果，卖出每千克水果盈利（毛利润）5元，每天可卖出1 000kg，经市场调查后发现，在进价不变的情况下，若每千克售价涨0．5元，每天销量将减少40kg．若以每千克盈利9元的价钱出售，则每天能盈利________元．若水果店想保证每天销售这种水果的毛利润为6 000元，同时又要使顾客觉得价格不太贵，则每千克水果涨价后的定价为多少元？......
2025-09-29
- 详细阅读
相关推荐