数据采集基本原理解析

2023-07-02 理论教育版权反馈

【摘要】：数据采集系统中采用计算机作为处理机。因此，在数据采集系统中同时存在着两种不同形式的信号：离散数字信号和连续模拟信号。为了避免产生上述问题，在对模拟信号离散化时，必须依据采样定理规定的原则进行。而脉冲函数：图3-4 采样过程原理图a）采样信号 b）脉冲函数2.采样定理对于一个有限频谱的连续信号，当采样频率大于信号成分最高频率的2倍时，采样才能不失真地恢复到原来的连续信号。采样定理是采样频率选取的理论基础。

数据采集系统中采用计算机作为处理机。众所周知，计算机内部参与运算的信号是二进制的离散数字信号，而被采集的各种物理量一般是连续的模拟信号。因此，在数据采集系统中同时存在着两种不同形式的信号：离散数字信号和连续模拟信号。在研究开发数据采集系统时，首先遇到的问题是传感器所测量到的连续模拟信号怎样转换成离散的数字信号。

连续的模拟信号转换成离散的数字信号，经历两个断续过程。

（1）时间断续

对连续的模拟信号f（t），按一定的时间间隔T，抽取相应的瞬时值（即离散化），这个过程称为采样。连续的模拟信号f（t）经过采样过程后转换为时间上离散的模拟信号（即幅值仍是连续的模拟信号），简称为采样信号。

（2）数值断续

把采样信号以某个最小数量单位的整数倍数来度量，这个过程称为量化。采样信号经量化后变换为量化信号，再经过编码，转换为离散的数字信号（即时间和幅值是离散的信号），简称为数字信号。

在对连续的模拟信号做离散化处理时，必须遵守一个原则，如果随意进行，将会产生如下一些问题：

1）可能使采样点增多，导致占用大量的计算机内存单元，严重时将因内存量不够而无法工作。

2）也可能使采样点太少，使采样点之间相距太远，引起原始数据值的失真，复原时不能复现出原来连续变化的模拟量，从而造成误差。

为了避免产生上述问题，在对模拟信号离散化时，必须依据采样定理规定的原则进行。

1.采样过程

采样器按预定的时间间隔对模拟信号离散化，从而把连续的模拟信号转化为离散的脉冲子样，再由模数转换器把离散子样进行量化和编码，变成数字信号送到存储器等待处理。采样过程原理如图3-4所示。

由于采样信号：

f_s（t）=f（t）δ（t）（3-1）

式中，f（t）为待采集的模拟信号；δ（t）为脉冲函数。

而脉冲函数：

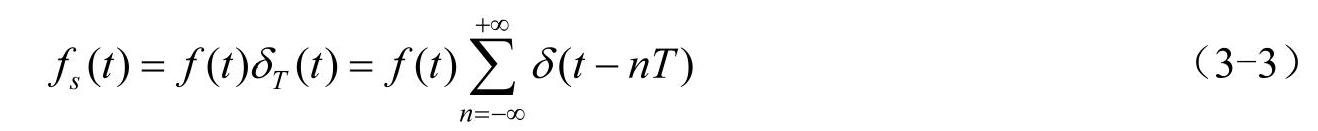
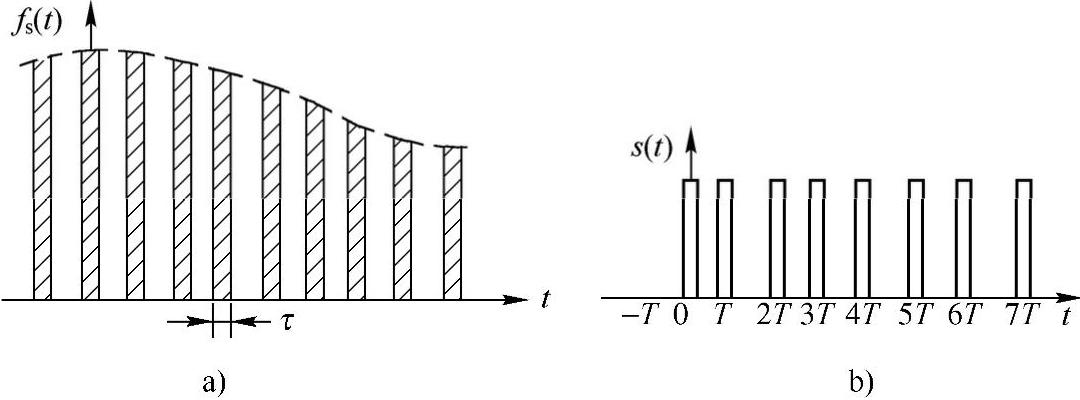
图3-4 采样过程原理图

a）采样信号 b）脉冲函数

2.采样定理

对于一个有限频谱的连续信号，当采样频率大于信号成分最高频率的2倍时，采样才能不失真地恢复到原来的连续信号。采样定理又称奈奎斯特（Nyquist）定理。采样定理是采样频率选取的理论基础。

一般地，信号的最高频率难以确定，当含有噪声时，则更为困难。采样理论要求在取得全部采样值后才能求得被采样函数，而实际在某一采样时刻，计算机只取得本次采样值和以前各次采样值，因此必须在以后的采样值尚未取得的情况下进行计算分析。因此，实际的采样频率取值高于理论值，一般为信号最高频率的5～10倍。

数据采集基本原理解析

相关推荐