算法根据决策变量X和式～式的约束条件依次确定任务续传调度标识符和相应的执行时间，从而得到决策变量X的目标函数。图9-27可用时间窗口更新交叉；嵌入；包含；无关确定所有任务的续传调度标识和执行时间后，计算目标函数F=｛f 1，f 2，f 3｝，即可评价此调度方案优劣。......
2023-07-02
多目标蚁群算法的设计与优化
【摘要】：为消除各类约束导致的大量任务间冲突，获得问题的Pareto解集，本书采用多目标蚁群算法优化任务的调度顺序。由于本章算法为多目标蚁群算法，因此本章算法采取与第3章的优化算法不同的启发策略。本章算法多目标蚁群算法采用自适应策略，在算法起始阶段，启发选择比例参数q 0［式（3-6）］取较大值利于加快收敛速度；在算法搜索后期，选择较小的q 0值可增加种群多样性。
为消除各类约束导致的大量任务间冲突，获得问题的Pareto解集，本书采用多目标蚁群算法优化任务的调度顺序。针对蚁群算法在应用过程中存在收敛慢、容易出现停滞现象、运算时间长等不足，引入自适应策略和小窗口思想改进蚁群算法，算法具体流程如图9-28所示。
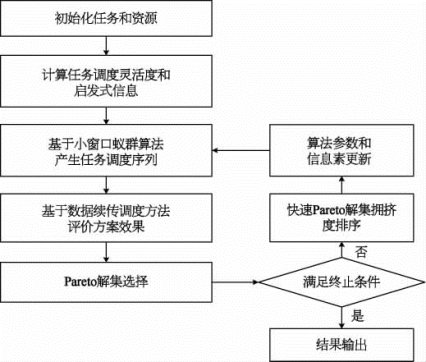
图9-28 算法流程
1）可行解构造
如图9-28所示，基于小窗口蚁群算法产生的任务调度序列即为问题的可行解，本算法可行解的构造与第3章ASAC-DLO算法的构造方法相同。由于本章算法为多目标蚁群算法，因此本章算法采取与第3章的优化算法不同的启发策略（最优解的选择和信息的更新）。
本章算法多目标蚁群算法采用自适应策略，在算法起始阶段，启发选择比例参数q 0［式（3-6）］取较大值利于加快收敛速度；在算法搜索后期，选择较小的q 0值可增加种群多样性。因此q 0大小在搜索过程中依下式自适应调整：
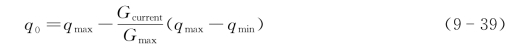
式中，G max为最大迭代次数，G current为当前代数，q max和q min分别为任务q 0的上下限。
2）Pareto解集拥挤度排序
设置外部Pareto解集S p保存当前已找到的Pareto解，基于Pareto解集定义选择当前蚁群与解集S p中的Pareto解，并更新外部最优解集S p。为避免算法对蚁群个体朝Pareto解过于密集的区域引导，而偏离Pareto解最前沿方向，不能对集合S p中所有Pareto解路径上的信息素加强。因此设置精英Pareto解集E p用于更新路径上的信息素，精英解集E p为集合S p中拥挤度最小的前N ep个个体。
常用的拥挤度计算方法需计算集合中所有个体间的距离，计算量较大，影响算法效率。采用一种快速的拥挤度计算方法，用来评估一个解周围其他解的密集程度。先根据每个目标函数的大小对Pareto解集中的解排序，对于每个解F i计算由解F i+1和F i-1构成的立方体的平均边长作为解Fi的拥挤距离D i，边界解（某个目标函数的最大值或最小值）的拥挤距离为无穷大。
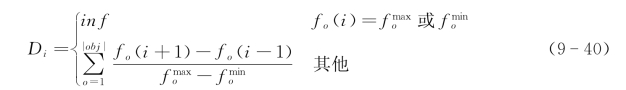
式中，
和
分别为第o个目标的最大值和最小值，｜obj｜为目标函数个数，个体的拥挤度为拥挤距离的倒数。
3）信息素更新策略
蚁群选择任务调度次序后将在路径上留下信息素，以指导子代蚁群寻优。设置任务间初始信息素为τ0，假设蚂蚁个数为N a，本算法采用全局信息素更新原则，更新规则为
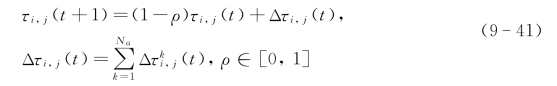
式中，τi，j（t+1）为第t+1代任务间信息素浓度，ρ为挥发系数，Δτi，j（t）为本次循环任务J i与J j间的信息素增量，算法采用Ant cycle模型［122］对每一代精英个体路径上的信息素增强，即
式中，Q为信息素增强系数。为避免算法过早收敛，将每代任务路径上的信息素限定在［τmin，τmax］区间内。
有关空间激光微波混合信息网络技术的文章
- 详细阅读
-
基于正交设计和蚁群算法的动态疏导模型提高城市详细阅读
而应用上节提出的基于正交设计的蚁群算法，可以构造L49 的正交表，产生49 个均匀分散、齐整可比的初始路径方案，并快速搜索得出其中的最优路径。表5-8交通事件影响评价指标对比表综合以上分析说明，应用基于正交设计及蚁群算法的动态疏导模型后的交通需求分配更为合理，疏散速度更快，有效地降低了研究路网的拥堵成本，进而提高了路网交通的运行效率。......
2023-09-26
-
多目标群体智能算法-多目标群体智能算法详细阅读
进化算法以其搜索的全局性逐渐成为解决MOP问题的有效工具。以下按照Coello Coello[14，15]的总结方式来简介多目标进化优化领域的一些代表性算法。第一代多目标进化算法1989年，Goldberg建议用非支配排序和小生境技术来解决MOP问题。第一代多目标进化算法以基于非支配排序的选择和基于共享函数的多样性保持为其主要特点，但这一代MOEA算法的缺点也十分明显。因此，第二代多目标进化算法普遍使用了精英策略。......
2023-11-26
-
多目标群体算法萤火虫算法详细阅读
萤火虫算法的核心思想是萤火虫被绝对亮度比它大的萤火虫所吸引，并根据位置更新公式更新自身的位置。考虑到萤火虫i的亮度随着距离的增加以及空气的吸收而减弱，可以定义萤火虫i对萤火虫j的相对亮度为:式(5.1)中，Ii为萤火虫i的绝对亮度，等于萤火虫i所处位置的目标函数值；γ为光吸收系数，可设为常数；rij为萤火虫i到萤火虫j的距离。γ为光吸收系数，表示吸引力的变化，它的值对萤火虫算法的收敛速度和优化效果有很大的影响。......
2023-11-26
-
蚁群算法原理及应用-城市道路交通事件影响分析详细阅读
蚂蚁系统是蚁群算法最原始的模型，也被称为基本蚁群算法，它是之后所有蚁群算法的原型。蚁群算法最初是由Dorigo M 等提出并应用于解决经典的TSP 问题，并取得了极好的效果。因此，本书将引入TSP 问题系统介绍基本蚁群算法的数学模型。Nothegger[21]、Dowsland[22]等人将蚁群算法应用于求解多种不同类型的指派问题，例如二次指派问题、频率指配问题及图形着色问题等。......
2023-09-26
-
多目标算法解决高维问题详细阅读
为有效求解高维多目标优化问题，研究者从不同的方面开展研究，概括起来可分成如下几类。使用改进的支配关系为提升Pareto支配关系在高维多目标优化问题上的选择压力，一些改进的支配关系陆续提了出来。Yuan等[54]将高维多目标降维问题视为一个3-目标的优化问题，并从维持解群的支配结构和目标相关性出发定义了目标函数。......
2023-11-26
-
多目标进化算法形式化描述详细阅读
下面介绍进化算法的相关定义和统一的描述框架[1]。对于各种进化计算方法，存在一个非空集合I，I称为这个进化计算的个体空间。D的值域确定了进化计算的实际搜索范围。随机函数被称为随机种群变换，其中Ω为采样空间。遗传算法是目前研究的进化算法中三种典型算法之一，其他两种分别是进化规划和进化策略。进化规划的特点在于没有使用交叉算子，采用随机选择机制，因而变异在进化过程中占据重要地位。......
2023-11-26
-
叶片泵设计简单算法的优化措施详细阅读
它是由SIMPLE算法的提出人之一Patanker完成的。将上述两方面的思想结合起来，就构成了SIMPLER算法。在SIMPLER算法中，经过离散后的连续方程式用于建立一个压力的离散方程，而不像在SIMPLE算法中用来建立压力修正方程。总体而言，SIMPLER的计算效率要高于SIMPLE算法。它也是SIMPLE的改进算法之一，是由Van Doormal和Raithby提出的。......
2023-06-26
相关推荐