Smith和Brady［171］提出的SUSAN算法是一种应用广泛的基于图像灰度变化的方法，随后出现的MIC算法［172］等都是它的思想的改进和发展。SUSAN算法就是根据各个待考察点的USAN区域面积来判断当前点是区域内部点、边界点还是角点。图4-7 USAN区域图解图4-8所示为SUSAN算法的三种近似圆形模板，在实际应用中，37邻域的7×7模板最为常用。灰度差阈值t决定了SUSAN算子所能检测到的最小的对比度以及去除噪声点的能力。......
2023-06-28
改进NSGA-Ⅱ的优化算法设计方案
【摘要】：MNSGA-Ⅱ具体流程如图9-12所示。MNSGA-Ⅱ以天线资源作为编码依据，在完成对任务的调度预处理之后，将任务所选择的天线资源序号作为种群内染色体基因。图9-13初始种群构造流程2）改进NSGA2算子设计快速非支配排序。
以传统NSGA中非支配排序和拥挤度排序思想为借鉴，同时引入基于精英保留策略的选择算子和混合交叉算子，提出了一种改进型非支配排序遗传算法（MNSGA-Ⅱ），用以解决混合系统资源调度问题，算法能够同时对于调度模型的多个目标函数进行优化寻优，并最终获得多目标优化问题的Pareto最优解集。MNSGA-Ⅱ具体流程如图9-12所示。
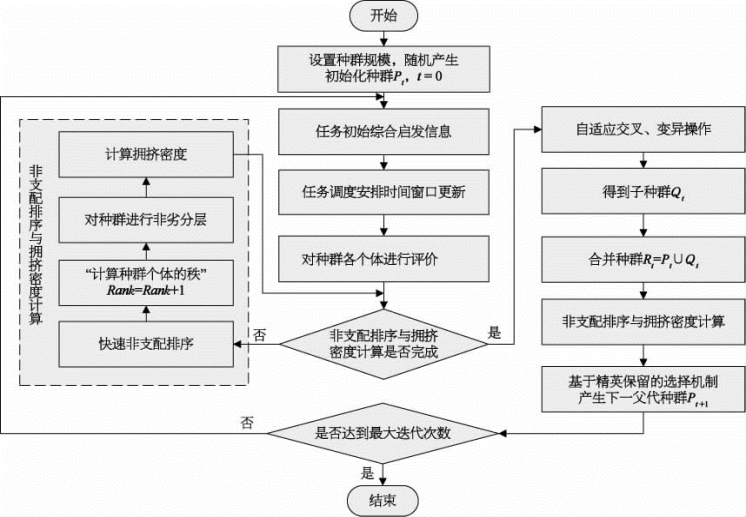
图9-12 算法流程
1）初始种群构造
算法的初始种群构造过程包括算法的编码和解码操作两部分。MNSGA-Ⅱ以天线资源作为编码依据，在完成对任务的调度预处理之后，将任务所选择的天线资源序号作为种群内染色体基因。其解码过程则是依据任务相应的天线资源，将任务安排在该资源的可见时间窗口内进行传输，若所在资源无法成功传输任务，则任务转入未调度任务序列。初始种群构造流程如图9-13所示。
图9-13 初始种群构造流程
2）改进NSGA2算子设计
（1）快速非支配排序。快速非支配操作的主要思想是依据多目标问题的目标函数值，对种群中个体执行非支配分层操作，即将当前所有非支配解都归为同一等级，直到所有个体都被分配到相应的非支配解集。具体流程如图9-14所示。
图9-14 快速非支配排序流程
（2）基于小生境尺寸的拥挤距离排序。多目标优化问题中，定义拥挤距离为解空间内一个解与其周围其他解之间的密集度，对于多目标问题中的目标函数，以该目标函数值为依据对非支配解集F i中的解排序，定义解i的拥挤距离为解i+1和i-1所围成立方体的平均边长。设目标函数个数m，第k个目标函数为f k，拥挤距离i distance定义为
式中，f k为最大值或最小值时，取其i distance为无穷大。i distance越大表明解i周围的点越稀疏，在种群进化过程中应对其以较大的概率保留至下一代，这样就能够从属于同一非支配前沿等级的所有解中选择拥挤距离较大的解参与到下一代运算中，从而保持种群多样性。拥挤距离排序基于拥挤比较算子（≻n），当且仅当“i rank＞j rank”或者“i rank=j rank且i distance＞j distance”时有i≻nj。
（3）混合交叉、变异算子。采用一种混合自适应交叉、变异方式，即针对不同种群内的个体分布情况，选取相应不同的交叉、变异概率进行操作，当种群内个体趋于一致时，P c和P m增大，防止了算法陷入局部最优。当种群内个体在解空间内分散时，P c和P m减小，使得优秀个体有更大的概率保留至下一代，提高了算法的快速收敛特性。
（4）基于精英策略的选择机制。算法采用父子竞争的选择机制，保留进化过程中的优秀个体进入下一轮的进化。具体方法是由两父代交叉产生新一代种群，然后合并父代与子代种群，对合并种群内的个体执行非支配排序操作，并分别计算其拥挤距离，最后依据拥挤比较算子选择优秀个体进入下一代，这样使得进化中的子代总是不劣于其父代，从而进化能够始终向着最优解发展。具体流程如图9-15所示。
图9-15 选择操作流程
有关空间激光微波混合信息网络技术的文章
- 详细阅读
-
城市旅游环境承载力评价与优化研究：NSGA-详细阅读
城市旅游环境承载力的优化是在旅游环境可持续利用的前提下，考虑旅游目的地经济效益、社会效益、环境效益的协调，得到合理的旅游环境承载力方案。根据NSGA-Ⅱ算法对旅游环境承载力优化模型求解，得出Pareto解集，为决策者提供参考。步骤4：检验是否满足终止条件，不满足则转步骤2，输出满足旅游环境承载力优化模型的Pareto解集。......
2023-10-29
-
改进仪表底盘级进模设计方案详细阅读
排样图：如图11-45b所示。图11-45 仪表底盘级进模a）制件图 b）排样图图11-45 仪表底盘级进模（续）c）模具结构图 1—凹模板垫板 2—卸料螺钉 3—下模顶块 4、8、9、10—凸模 5—上模顶块 6、14—弹簧 7—成形凸凹模 11—侧刃凸模 12—凹模板 13—下模座 15—弹簧顶杆 16—弹簧顶板说明：1）该模具为冲孔、切口、落料、成形等3个工位的级进模结构。3）该制件翻边后的最大高度为10mm。......
2023-06-26
-
改进微形网孔级进模设计方案详细阅读
图11-1 微形网孔级进模a）制件图 b）排样图图11-1 微形网孔级进模（续）c）模具结构图 1—上模座 2—导套 3、9—小导柱 4、10、17、23—小导套 5—固定板 6、7—凸模 8、24、27—螺钉 11、16—圆柱销 12—保持圈 13—导柱 14—下模座 15—下模板垫板 18—下模板 19—凹模 20—导料板 21—承料板 22—卸料板镶件 25—卸料板 26—卸料板垫板 28—固定板垫板说明：1）该模具为一出四微形网孔自动冲孔的级进模结构。......
2023-06-26
-
起飞方式的优化与改进详细阅读
图4.4 美国加利福尼亚州空军基地进行跑道测试的全球鹰对于大型固定翼无人机而言，完全可以采用常规飞机的起飞方式。弹射起飞方式有利于将更大型的无人机部署到更多地点，如山地、航母等。图4.6 渡鸦无人机抛飞与检查手抛起飞一直是小型固定翼飞机的重要起飞方式。）传统固定翼无人机的起飞方式就是以上几种。......
2023-07-05
-
量子遗传优化算法的优化方法详细阅读
量子遗传算法是一种将遗传算法和量子计算相结合的概率优化方法，两者相互作用。量子遗传算法是一种将量子比特的概率幅用于染色体编码，用量子门的调整操作来实现染色体更新，以完成进化搜索的方法。量子遗传算法的流程如下：初始化种群Q，随机生成n个用量子比特编码的染色体。......
2023-06-29
-
中文分词算法的优化策略详细阅读
一般来说，中文分词在具体的算法实现上分为三种：基于字符串匹配的分词方法、基于理解的分词方法和基于统计的分词方法。在中文搜索引擎中，目前基本上是这三种算法混合使用。2）基于统计的分词方法基于统计的分词方法也叫最大概率分词方法。作为中文分词基础的词库，新词补充和老词删除就是非常重要的工作。比如“测试”在“每台计算机在出厂前都要经过严格的测试”这句话中是典型的动词，而在“软件测试领域”中是一个名词。......
2023-07-02
-
虚拟现实应用中的辐射度算法及其改进方法详细阅读
辐射度的算法分为三个步骤［26］。两个patch之间的形式因子表示了一个patch出射的光有多少比例会被另一个patch接收。辐射度算法会非常的慢，而且如果不考虑额外的复杂度，辐射度算法很难计算镜面反射，改进的辐射度算法可以缓解这一问题。很多研究者都试图结合光线追踪和辐射度这两种方法，以期达到各自的优势。对于，我们收集来自caustics map中的光子信息。即使是photon map算法，对于普通硬件，暂时也只能用于静态渲染。......
2023-10-17
相关推荐