基于Pareto优化的多目标搜索策略

2023-07-02 理论教育版权反馈

【摘要】：图9-10MOEA算法框架9.5.1.2NSGA与NSGA-Ⅱ算法NSGA是多目标进化算法发展过程中非常重要的算法，NSGA-Ⅱ为其改进版本，下面分别描述这两种算法。1）非支配排序遗传算法基于Goldberg的方法，NSGA对个体分类，形成多个层次。NSGA具有非支配最优解分布均匀，同时允许存在多个不同等效解的优点。

9.5.1.1　多目标进化算法

在多目标优化问题中，通常存在着多个相互矛盾的目标，如何在多个目标冲突的条件下获得问题最优解，是学术研究与工程应用领域中关注的焦点。通常MOEA算法要求能够提供一组尽可能多的非支配解，并且这组解能够逼近问题的全局Pareto最优前端，且在全局最优前端上均匀分布。大多数多目标进化算法都是针对这3个要求的特定方法的有效组合。

MOEA的主要模型由Laumanns等人提出，其流程如图9-10所示，设定初始种群与初始第二种群，依据种群和第二种群中的非支配解对第二种群内的个体进行更新操作。为了提高算法的搜索效率，在每一代种群中，当第二种群中的非支配解超出规定的数值时，就对第二种群进行修剪操作。对种群中的个体赋予相应的适应度值，进行选择操作挑选个体进入下一代种群，再对种群进行交叉和变异等操作。

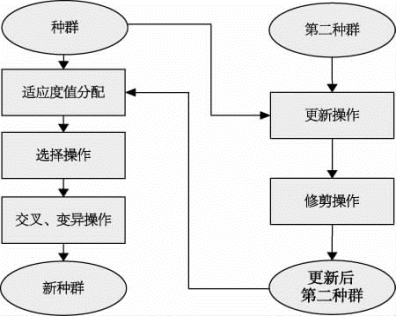
pagenumber_ebook=347,pagenumber_book=333

图9-10　MOEA算法框架

9.5.1.2　NSGA与NSGA-Ⅱ算法

NSGA是多目标进化算法发展过程中非常重要的算法，NSGA-Ⅱ为其改进版本，下面分别描述这两种算法。

1）非支配排序遗传算法

基于Goldberg的方法，NSGA对个体分类，形成多个层次。具体过程为：在选择操作之前，基于Pareto最优对个体进行排序操作，所有非支配的个体归为一类，通过将共享函数法引入算法来保持种群的多样性；然后，保留已完成分类的个体，考虑另一层非支配的个体；反复执行此操作直到将所有个体完成分类。由于最先得到的非支配个体具有最大的适应度值，因而具有最大的被复制概率。

NSGA具有非支配最优解分布均匀，同时允许存在多个不同等效解的优点。而由于算法中Pareto排序操作要多次重复执行，算法计算效率较低，计算复杂度很大，并且算法未采用精英保留策略，其中的共享函数σshare也需要预先确定。

2）非支配排序遗传算法Ⅱ

NSGA-Ⅱ作为传统非支配排序遗传算法的改进版本，在其进化过程中，子代种群Q通过对父代种群P执行交叉、变异操作得到，父代与子代组成联合种群，通过非支配排序和拥挤距离排序操作，其中的优秀个体被保留至下一代，重复进行此操作，当算法满足结束条件时停止。算法流程为：

（1）对随机产生的初始种群Pt执行非支配排序操作，依据适应度值将种群内个体分为不同等级并赋予相应的秩；父代种群P t通过遗传过程中的选择、交叉和变异操作可获得子代种群Qt，令迭代计数器t=0。

（2）将父代和子代种群合并得到联合种群Rt=Pt∪Qt，对新种群Rt执行非支配排序操作，获得种群的非支配前端F 1，F 2，…

（3）对于非支配前端F i中个体，通过执行拥挤度比较操作，选择其中前N个优秀个体进入下一代，形成新的父代种群P t+1。

（4）父代种群Pt+1通过遗传过程中的选择、交叉和变异操作获得子代种群Qt+1。

（5）判断算法是否达到最大迭代次数，若达到则算法结束；否则令t=t+1，转入步骤（2）NSGA-Ⅱ主要算法流程如图9-11所示。

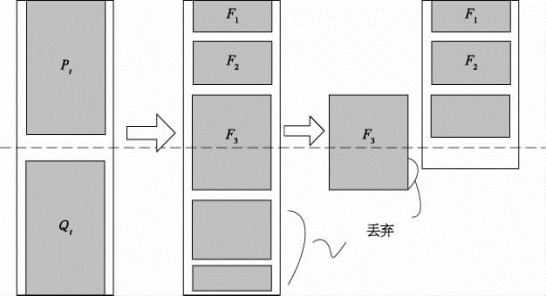
pagenumber_ebook=348,pagenumber_book=334