然后，提出一种基于空时相关系数的特征选取方式替代传统的信道特征，并对天线选择方案做分解，以使得DNN模型能够有更好的拟合效果。......
2023-08-23
基于精英保留的自适应小生境遗传算法
【摘要】：智能优化求解模型中主体部分是基于精英保留策略的自适应小生境遗传算法，算法基本流程步骤为：Step1：种群初始化。遗传算法中种群的每个个体代表问题的一个解，称为染色体。自适应交叉、变异算子将自适应策略引入标准遗传算法中实现交叉和变异操作，因此，变异、交叉概率能够随种群个体适应度值变化而动态改变。
智能优化求解模型中主体部分是基于精英保留策略的自适应小生境遗传算法，算法基本流程步骤为：
Step1：种群初始化。已知M为种群规模，Max为最大迭代次数，P c和P m分别为交叉及变异概率，k为迭代次数计数器。利用小生境淘汰操作在随机产生2M个个体中选出前M个构成初始种群，令k=1。
Step2：适应度值计算。对于种群中个体计算其相应适应度值、种群平均适应度值f avg和最小适应度值f min，按照适应度值降序排列个体，再进行基于精英保留的选择操作。
Step3：交叉、变异操作。根据自适应交叉、变异算子计算相应的P c和P m，按照适应度值降序对经过选择、变异和交叉操作之后获得的M个个体进行排序。
图9-5 同一资源上任务的调度流程
Step4：小生境淘汰操作。对于Step3中获得的个体，确定小生境距离参数L，通过对比个体上等位基因来判断个体的相似度，若相似度过高，即个体相似度大于平均值，则采用罚函数策略淘汰其中适应度较小的个体，同时产生与淘汰个体数同等的新个体，加入到种群进化过程中。
Step5：算法终止条件判断。判断是否达到最大迭代次数，如未达到则更新数据，令k=k+1，将Step4中M个个体作为新个体转入Step2；如果达到最大迭代次数则算法结束，输出调度结果。
具体的算法设计：
（1）染色体编码。遗传算法中种群的每个个体代表问题的一个解，称为染色体。本算法中采用天线终端的染色体表现形式，即将任务选择的天线终端序号作为染色体上基因。
算法的编码过程：获取所有的任务序列及其相应的优先级权值，按照优先级权值降序的规则对所有任务进行排序操作，对任务序列随机分配终端天线，产生初始种群。
（2）适应度值函数。对于混合系统中的目标函数进行线性加权运算，定义加权和结果为算法的适应度值函数为
其中设目标函数为k个，分别定义目标函数i的无量纲标准化值和相应的优先级权值为
和w i。由适应度值函数定义式可知，适应度值越小，即调度结果中未调度任务总权值越小、天线终端功耗越少，所有任务传输完成时间越短，则该个体就越优秀。
（3）基于精英保留策略的选择机制。与大多数单纯依据适应度值确定个体遗传概率的选择方法不同，本书通过具有精英保留策略的二元锦标赛方法来确定个体保留至下一代的概率。具体选择方法为：经过小生境淘汰操作后，种群内保留的个体数为M个，分别计算M个个体的适应度值，并通过随机设置个体对，对于种群内个体进行两两比较，其中适应度值较小的个体直接保留至子代进行下一步进化操作，同时其个体适应度值被记忆，而不再重复计算，造成资源的浪费，从而提高算法计算效率。
（4）自适应交叉、变异算子。采用混合的自适应交叉、变异算子，在进化过程初期，按照固定的交叉和变异概率执行遗传操作，在进化过程后期，则按照自适应交叉、变异算子执行遗传操作。自适应交叉、变异算子将自适应策略引入标准遗传算法中实现交叉和变异操作，因此，变异、交叉概率能够随种群个体适应度值变化而动态改变。其主要思想是当种群中个体趋于一致时，增大遗传操作中的交叉概率P c和变异概率P m，可及时避免算法陷入局部最优；当个体在约束空间内分别较分散时，减小P c和P m，能够使得算法快速收敛，降低计算量。
设种群个体的平均和最小适应度值分别为f avg和f min，交叉个体平均适应度值为f c，变异个体适应度值为f m，取k 1，k 2，k 3，k 4为范围在（0，1）之间的常数，自适应交叉、变异算子为
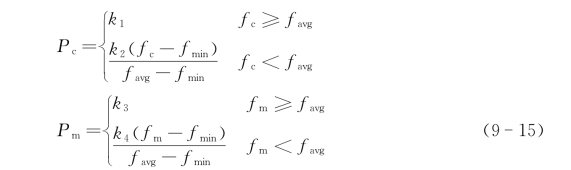
由上式可以看出，P c和P m在个体适应度值低于平均适应度值时取值较小，而在个体适应度值高于平均适应度值时取值较大，这样交叉、变异概率的动态改变不仅有利于种群中优秀个体保留至下一代，而且增大了新个体产生的概率，能够有效避免算法陷入局部最优。
（5）小生境淘汰操作。定义小生境距离参数L为种群内前N个优秀个体之间的最小欧式距离，如式（9-16）所示，定义个体x i和x j，染色体长度为length。L随着每一代个体的不同而实时动态变化，依据不同的距离参数进而获得合理分布的小生境环境。
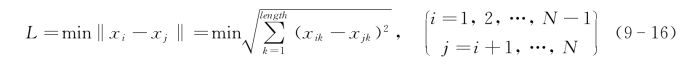
同时为避免算法陷入局部最优，定义个体之间相似度为相同等位基因数除以染色体上总基因数，定义平均相似度为个体i与其他个体直接相似度之和除以个体数减1。根据小生境距离内的个体相似度，可以对较差个体实施淘汰操作，从而得到在约束空间内均匀分布的个体。
有关空间激光微波混合信息网络技术的文章
- 详细阅读
-
基于轴辐网络的应急设施布局优化理论与应用-遗详细阅读
遗传算法对问题的可行解进行编码，通过适应度函数构成优胜劣汰、适者生存的“自然环境”，种群通过遗传、交换、突变等不断演化，产生出新的更加优良的种群，这样经过若干代的进化，最终求得问题的最优解。遗传算法步骤[103]如下：STEP1：选择问题的一个编码；给出一个有N个染色体的初始群体POP，t=1；STEP2：对群体中POP中的每一个染色体popi计算它的适应度函数，fi=fitness[popi]；STEP3：若停止规则满足，则算法停止；否则，计算概率；，2，…......
2023-09-19
-
自适应阈值改进的SUSAN算法详细阅读
Smith和Brady［171］提出的SUSAN算法是一种应用广泛的基于图像灰度变化的方法，随后出现的MIC算法［172］等都是它的思想的改进和发展。SUSAN算法就是根据各个待考察点的USAN区域面积来判断当前点是区域内部点、边界点还是角点。图4-7 USAN区域图解图4-8所示为SUSAN算法的三种近似圆形模板，在实际应用中，37邻域的7×7模板最为常用。灰度差阈值t决定了SUSAN算子所能检测到的最小的对比度以及去除噪声点的能力。......
2023-06-28
-
遗传算法优化问题求解详细阅读
遗传算法的这些性质，已被人们广泛地应用于组合优化、机器学习、信号处理、自适应控制和人工生命等领域。遗传算法之所以具备强大的搜索能力，是因为包罗了选择、杂交和变异三种基本操作算子，同时这三种操作算子也是模拟自然生物圈中自然存在的有性繁殖、杂交和变异等现象的核心载体。同样，遗传算法中起核心作用的是遗传操作的交叉算子。通过交叉，遗传算法的搜索能力得以飞跃提高。图11-1遗传算法流程图......
2023-06-28
-
巧吃猪肉，保留更多营养详细阅读
事实上，完全不吃肉，人体就会因此缺乏很多营养元素，如维生素B12，它在猪肉等动物性食物里很丰富，而在植物性食物中却很少。至于“瘦肉精”、猪饲料添加剂等造成的猪肉质量问题，的确存在，但并没有那么严重，只要我们小心地挑选猪肉，充分地予以加工，还是可以适当避免的。......
2023-08-15
-
保留IP地址及其特殊用途详细阅读
在IP地址中，有些IP地址是被保留作为特殊用途的，不能用于标志网络设备，这些保留地址空间如下。回送地址A类网络地址127.0.0.0是一个保留地址，也就是说任何一个以127开头的IP地址均为一个保留地址，用于网络软件测试以及本地机器进程间通信。这个IP地址叫作回送地址，最常见的表示形式为127.0.0.1。在每个主机上对应于IP地址127.0.0.1有个接口，称为回送接口。......
2023-11-04
-
启发式遗传算法的流程设计详细阅读
具体的遗传算法流程如图5-6 所示， 分为种群初始化、 选择和复制、 交叉、 变异与终止几个步骤：种群初始化。遗传算法中起核心作用的交叉算子， 特点是能使父串的特征遗传给子串， 子串应该能够部分或者全部地继承父串的结构特征和有效基因。图5-6启发式遗传算法流程图终止。针对纳什平衡求解问题， 运用启发式遗传基因算法进行寻优。......
2023-06-20
-
争风吃醋隐秘之事保留官位的生存术详细阅读
从此，何与宣公开成双出入，何敏俨然成了宣铁吾的二太太。某日晚上，宣铁吾携何敏到军人俱乐部看戏，叶跟踪而至。宣铁吾当众受辱，恼羞成怒，提笔写了张便条，命人送往军警稽查处。该报社副社长刘湘女见了这则启事，急忙来见宣铁吾，劝宣不要刊登，以免家丑外扬，影响宣的名誉和国民党的形象。事后，宣又电告蒋介石，请求辞职。......
2023-08-07
相关推荐