生态效益子目标是指通过水沙资源的优化配置，减轻水沙不合理利用引起的环境污染和恶化，尽可能利用水沙资源改善生态环境，促进河流健康发展。经济效益子目标是指水沙资源优化配置要节省有限的水资源，配置措施要尽可能节省人力物力，泥沙资源利用还要注重创造经济收入。表12-2黄河下游泥沙资源配置目标层次分析......
2023-06-23
多目标优化的基本原理详解
【摘要】：“min／max”表明目标函数可以为最大化或者最小化。与单目标优化问题相比，多目标优化问题更加复杂。在具有多个目标函数的优化问题中，通常存在有一组无法进行相互比较的解，而不存在唯一最优解，因此多目标优化问题的最优解是一组折中解，称为非支配解或Pareto最优解。图9-2非支配解及Pareto前沿3）偏好结构多目标优化问题的求解中通常存在一组无法进行相互比较的解，取这组解中符合决策者偏好的最优解为最终决策结果。
1）多目标优化问题
单目标优化问题可表示为
式中，x∈Rn表示具有n个决策变量的向量，f（x）为目标函数，gi（x）为约束条件，由目标函数和约束条件就构成了可行解区域。“min／max”表明目标函数可以为最大化或者最小化。为方便统一，本节讨论问题都是最小化目标问题。在决策空间中，可行区域通常用S来表示：
多目标问题通常表述为
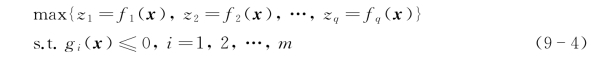
多目标优化问题需要在决策空间和判据空间中用图像表示，其中决策空间中的可行区域用S表示，判据空间中的可行区域用Z表示：
式中，z∈Rq表示具有q个目标函数的向量。Z表示S中点的像的集合，因此S限制为Rn上的非负象限，而Z却没有限制。
与单目标优化问题相比，多目标优化问题更加复杂。当问题具有单个目标函数时，优化目标是找寻最优解，最优解要优于其他所有的解。当问题具有多个目标函数时，如果问题中的多个目标函数彼此不矛盾，显然可以通过单目标优化方法找到唯一的最优解满足各目标函数都达到最优。而优化问题中的各目标之间往往无法通过统一标准进行比较，甚至彼此矛盾，所以在各目标函数都取最优的解不一定存在，本节所研究问题模型中的目标函数即是彼此矛盾冲突的。
2）多目标优化问题解的概念
多目标优化问题与单目标优化问题之间差异较大。单目标优化问题具有确定的唯一最优解。在具有多个目标函数的优化问题中，通常存在有一组无法进行相互比较的解，而不存在唯一最优解，因此多目标优化问题的最优解是一组折中解，称为非支配解或Pareto最优解。在此给出多目标优化问题中的重要概念Pareto支配及相应多目标优化解的概念。
定义1.1：（Pareto支配）称向量u=（u 1，…，u k）支配向量v=（v 1，…，v k），当且仅当∀i∈｛1，…，k｝，u i≤v i且存在j∈｛1，…，k｝，使得ui＜v i成立。
由以上定义可得：
定义1.2：（Pareto最优解）称决策变量x*∈S⊂Rn为Pareto最优解，当且仅当不存在另一个决策变量x∈S使得F（x）支配F（x*），即F（x）≺F（x*）。
由Pareto最优解构成Pareto最优解集P*，F（P*）=｛F｜x∈P*｝为多目标问题的Pareto前沿，如图9-2所示。
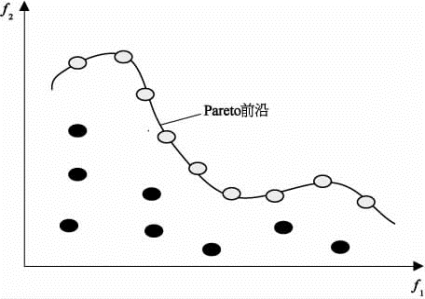
图9-2 非支配解及Pareto前沿
3）偏好结构
多目标优化问题的求解中通常存在一组无法进行相互比较的解，取这组解中符合决策者偏好的最优解为最终决策结果。偏好定义为依据决策者对目标重要性判断对非支配解的排序结果，可以是对某一目标的侧重或是所有目标的妥协。决策的过程即为根据决策者的给定偏好将非支配解进行排序操作，获得最终解也称最优妥协解。
对于解u和v，两者之间的偏好关系可以用一组关系来表示：
（1）u优于v，则称对u的偏好比v大，记为u≻v。
（2）v优于u，则称对v的偏好比u大，记为u≺v。
（3）u与v相等，则称u与v具有同等偏好，记为u～v。
（4）两者之间偏好未定义，记为u？v。
有关空间激光微波混合信息网络技术的文章
- 详细阅读
- 详细阅读
-
点焊的基本原理详解详细阅读
点焊接头是在热-机械（力）联合作用下形成的。点焊时的加热是建立焊接温度场，促进焊接区塑性变形和获得优质连接的基本条件。例如，低碳钢点焊质量监控中的“动态电阻法”。由于Q2、Q3的强烈作用，离开熔核边界温度降低很快。塑变能与热能使接触点的原子不断激活，接触面消失，继续加热形成熔化核心，简称熔核。图2-2-8f表示优质接头的熔核柱状组织示意图，断口形貌......
2023-06-26
-
外特性控制的基本原理详解详细阅读
图4-8为电子控制型弧焊电源外特性控制的基本原理图。图4-8 电子控制型弧焊电源外特性控制基本原理根据图4-2，可以得到控制信号Uk的数学表达式：Uk=K3[K1+K2] （4-7）式中 K1、K2、K3——系统中各个放大环节的放大倍数。此种外特性控制可以用于熔化极气体保护焊的恒压外特性控制中，对电源输出的最大电流进行限制。这种控制常用于焊条电弧焊恒流外拖特性的控制中。表4-1列出了常用弧焊电源外特性形状与选用的负反馈控制之间的关系。......
2023-06-30
-
基于Pareto优化的多目标搜索策略详细阅读
图9-10MOEA算法框架9.5.1.2NSGA与NSGA-Ⅱ算法NSGA是多目标进化算法发展过程中非常重要的算法，NSGA-Ⅱ为其改进版本，下面分别描述这两种算法。1）非支配排序遗传算法基于Goldberg的方法，NSGA对个体分类，形成多个层次。NSGA具有非支配最优解分布均匀，同时允许存在多个不同等效解的优点。......
2023-07-02
-
多目标蚁群算法的设计与优化详细阅读
为消除各类约束导致的大量任务间冲突，获得问题的Pareto解集，本书采用多目标蚁群算法优化任务的调度顺序。由于本章算法为多目标蚁群算法，因此本章算法采取与第3章的优化算法不同的启发策略。本章算法多目标蚁群算法采用自适应策略，在算法起始阶段，启发选择比例参数q 0［式（3-6）］取较大值利于加快收敛速度；在算法搜索后期，选择较小的q 0值可增加种群多样性。......
2023-07-02
-
多目标蚁群算法模型优化详细阅读
算法根据决策变量X和式～式的约束条件依次确定任务续传调度标识符和相应的执行时间，从而得到决策变量X的目标函数。图9-27可用时间窗口更新交叉；嵌入；包含；无关确定所有任务的续传调度标识和执行时间后，计算目标函数F=｛f 1，f 2，f 3｝，即可评价此调度方案优劣。......
2023-07-02
-
基于理想解的多目标决策优化详细阅读
为权衡目标间的关系，采用逼近理想解的排序方法获得问题的最佳解。TOPSIS方法的基本思想是：对多目标分类成效益型指标和成本型指标，并构造正负理想解；计算每个非劣解到正负理想解的相对距离并排序，选择相对距离最大的解即为最优解。，n）为非劣解，代表着n种不同的动态调度方案；f i分别为3个不同目标值：动态调度方案优先值收益o、加权方案变化δ和总加权续传次数c。......
2023-07-02
相关推荐