目前有大量文献针对最小生成树的构造问题进行研究。Zhou等人基于BUA算法，提出了节点自由度约束下的具有最大代数连通度的生成树算法。近年来，除了在网络中寻找具有最小开销的连通链路之外，最小生成树也在其他领域发挥了重要的作用。......
2023-07-02
节点数量、节点自由度限制和节点连通度需求对算法的影响
【摘要】：图6-4给出了3种仿真场景下算法得到的最重拓扑，图，，表示3种仿真场景中运行DMST算法得到的近似最优的最小生成树，图，，表示对应的CG算法的结果。在仿真中，仅考虑RC中的可行解来与CG算法比较。图6-7给出了两种算法在3种仿真场景中的运算结果。
为了考察提出的算法在不同拓扑环境中的性能，定义3种典型的场景来分析不同参数（比如节点数量、节点自由度限制和节点连通度需求）对算法的影响。这3种典型场景包括：
（1）第一个场景如图6-3（a）所示，考虑一个低轨道卫星网络，根据其构型规则，易判断算法结果的正确性。轨道内和轨道间的单跳星间距离变化情况如图6-3（b）所示。
（2）第二个场景如图6-3（c）所示，考虑一个位于同步地球轨道的空间信息网络。星群内和星群间的单跳星间距离变化情况如图6-3（d）所示。
（3）第三个场景如图6-3（e）所示，考虑一个多层空间信息网络系统，包括一个低轨道卫星网络、一个同步地球轨道的空间信息网络和两个位于中轨道的卫星星座。由于星间距离较多，在图6-3（f）中描述3条有代表性的星间距离变化情况。
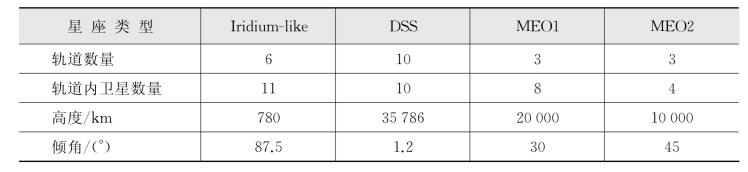
场景中的轨道参数如表6-5所示。由于轨道分布和轨道内的卫星节点分布都是均匀的，对算法结果没有影响，因此忽略了近地点幅角、真近点角和升交点赤经3个参数。
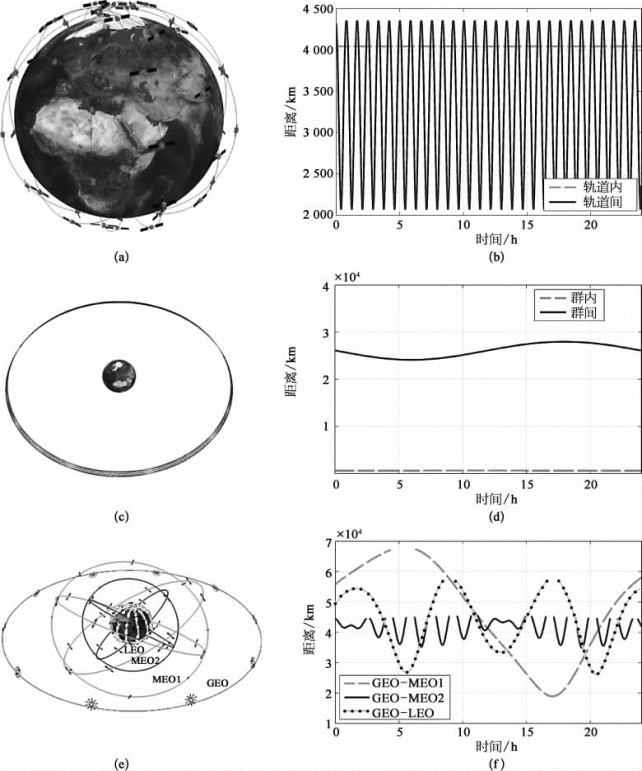
图6-3 3种典型场景和部分对应的星间距离变化情况
（a）低轨卫星网络轨道分布示意图；（b）同轨和异轨星间距离变化情况；（c）同步轨道星群网络轨道分布示意图；（d）星群内和星群间星间距离变化情况；（e）多层空间信息网络轨道分布示意图；（f）部分异轨星间距离变化情况
表6-5 仿真环境中的卫星节点轨道参数
上述场景均通过STK进行卫星星座构型的建模，通过Matlab进行算法的运算，其中的最优化部分采用CVX工具包进行求解。首先考察DMST和CG算法的正确性。假设ci=d i=4，∀i和t thr=300 s。图6-4给出了3种仿真场景下算法得到的最重拓扑，图（a），（c），（e）表示3种仿真场景中运行DMST算法得到的近似最优的最小生成树，图（b），（d），（f）表示对应的CG算法的结果。图中灰色的边表示运行CG算法时添加的边。从图中可以看出，通过DMST算法，3个场景下均能得到生成树，而运行CG算法后每个节点的连通度都达到了4。
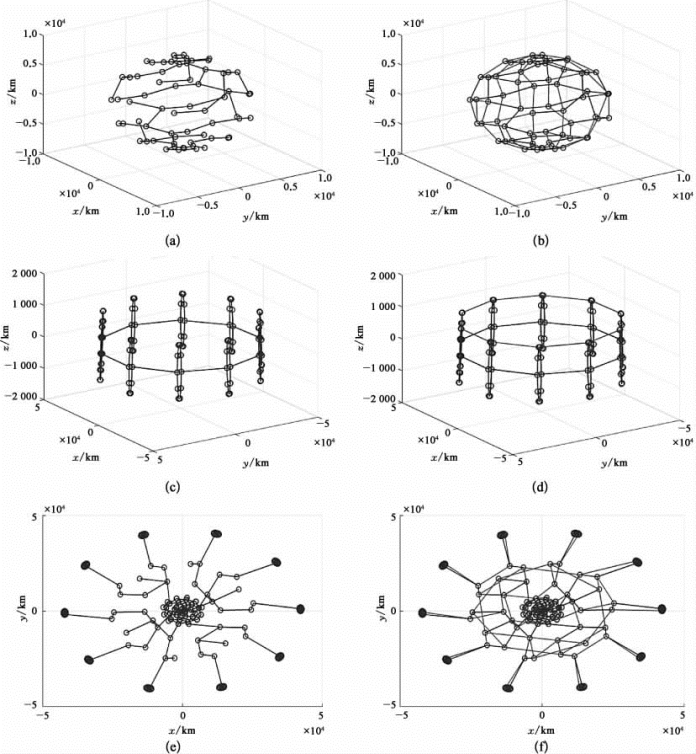
图6-4 3种场景下DMST和CG算法得到的拓扑结果
（a）低轨卫星网络的最小生成树；（b）低轨卫星网络连通度保证算法运行结果；（c）同步轨道星群网络的最小生成树；（d）同步轨道星群网络连通度保证算法运行结果；（e）多层空间信息网络的最小生成树；（f）多层空间信息网络连通度保证算法运行结果
接下来，考察提出的DMST算法在生成树的链路平均权重方面的性能，即算法的最优性。仍然假设每个节点的自由度为d i=4，∀i。为了比较算法性能，采用地面自由空间光通信网络中的自底向上算法（BUA）作为参考。分别采用这两种算法分析3种场景下0～24 h中最小生成树的演化情况，每个整点时的链路平均权重如图6-5所示。可以看出，DMST算法的性能显著优于BUA算法，且性能更加稳定，在3种场景中，分别达到了约7.03%，2.95%，9.47%的平均性能提升。
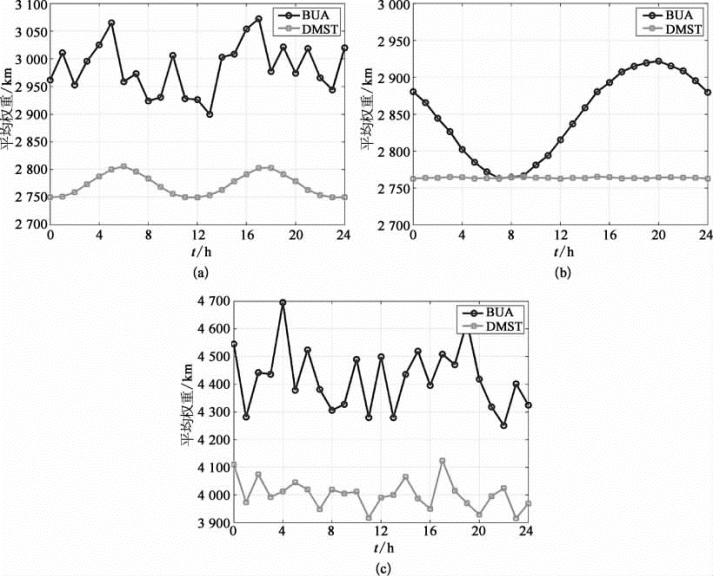
图6-5 不同场景中DMST与BUA算法链路平均权重性能对比
（a）低轨卫星网络；（b）同步轨道星群网络；（c）多层空间信息网络
进一步考察节点自由度对DMST算法链路平均权重性能的影响。图6-6表示节点自由度从2～10时DMST算法得到的网络拓扑的链路平均权重。图中的每个值是算法运行24 h之后的平均值。可以看出，除了d i=2，即节点自由度过小时，链路平均权重较大，其他各种情况下3种场景均维持了稳定的链路平均权重。这说明：一方面当d i=2时，最小生成树仅能表现为一个线型拓扑，几乎没有可供选择的链路来降低平均权重；另一方面，该仿真结果也表明了算法的稳定性较好，能够在自由度不高的环境中仍然构建出性能良好的最小生成树。
图6-6 DMST算法在不同节点自由度条件下的链路平均权重性能
最后，考察在不同的节点连通度需求下，采用CG算法构建的网络拓扑中链路平均权重的变化情况。选用一种迭代随机连接算法作为参考来对比提出的算法的性能，所谓迭代随机连接（RC）指的是每次迭代时随机选择一条链路加入当前的拓扑之中，直至所有的节点连通度需求得到满足。事实上，可以看出迭代随机连接算法在节点自由度不远大于节点连通度需求时，往往无法满足节点连通度需求，即无法得到问题的可行解。在仿真中，仅考虑RC中的可行解来与CG算法比较。图6-7给出了两种算法在3种仿真场景中的运算结果。可以看出，通过CG算法得到的拓扑结构具有远小于RC算法对应的链路平均权重。与RC算法相比，当分别取d i=3，4，5时，在第一个场景中，CG算法分别降低了约9.57%，16.27%，18.94%的链路平均权重；第二个场景中分别降低了约78.42%，87.16%，92.37%；而第三个场景中分别降低了约68.15%，78.06%，80.93%。因此，证明了CG算法具有稳定的拓扑构建能力和较低的链路平均权重。
图6-7 不同自由度条件下CG算法与RC算法链路平均权重性能对比
（a）低轨卫星网络；（b）同步轨道星群网络；（c）多层空间信息网络
有关空间激光微波混合信息网络技术的文章
- 详细阅读
-
空间信息网络中节点连通度保证算法的描述详细阅读
在空间信息网络中，由于星群节点的异构性，不同的节点可能需要不同的连通度来满足不同任务的需要。然而，在一个生成树中，节点的连通度几乎肯定是无法保证的。因此在本节中，将基于一棵最小生成树，通过提出的连通度保证算法，在网络中增加某些额外的边来满足节点连通度的需求，同时算法还需要保持网络中的平均链路权重尽量地小。表6-4节点连通度保证算法伪代码（续表）......
2023-07-02
-
节点损伤对结构的影响详细阅读
在上述结构损伤量化公式的推导中，并未考虑钢架结构中大量存在的各类节点及其损伤对于结构损伤的影响。当涉及多个构件连接处的端部时，节点自身的转动刚度同时受其远端支撑情况的影响。由式可见，框架节点的弯矩分配系数由连接于节点的各构件远端支撑条件决定。同时，当节点刚度因节点损伤发生变化时，则需考虑节点处的损伤对于结构层次损伤的影响。......
2023-08-26
-
满足节点连通度需求的最小链路平均权重算法比随详细阅读
提出的满足节点连通度需求的链路平均权重最小化算法与随机连接算法相比，当取节点自由度分别为3，4，5时，在低轨道卫星网络中，提出的算法分别降低了约9.57%，16.27%，18.94%的链路平均权重；在同步轨道星群网络中分别降低了约78.42%，87.16%，92.37%；而在多层空间信息网络中分别降低了约68.15%，78.06%，80.93%。......
2023-07-02
-
节点电流定律（KCL）的解析详细阅读
若约定背离节点的电流为正，指向节点的电流为负时，KCL仍不失其正确性，会取得相同的结果。只有在参考方向选定之后，才能确立各支路电流在KCL方程式中的正、负号。图1.5[例1.1]图KCL虽然是对电路中任一节点而言的，根据电流的连续性原理，它可推广应用于电路中的任一假想封闭曲面，如图1.6所示。......
2023-06-24
-
空间信息网络下的节点逐边调整算法详细阅读
图的拉普拉斯矩阵及特征值在数学领域有着广泛的研究，尤其是在采用图论和数学规划方法解决网络拓扑构型问题方面。图5-2位于不同轨道的3颗卫星组成的星间组网系统轨道分布情况；星间距离和可视性关系变化规律本章主要考虑空间信息网络中节点分布高动态和节点运算能力有限等星上系统的特点，针对网络初始化和网络重构两种典型场景，通过对拉普拉斯矩阵特征值在矩阵摄动条件下演化规律的分析，得出一种新的逐边调整的启发式算法。......
2023-07-02
-
DeviceNet节点开发步骤详细阅读
大多数DeviceNet产品只具备从机的功能，开发从机功能产品第一个要考虑的问题是I/O通信。DeviceNet规范允许所有四种连接方式：迷你型接头、微型接头、开放式接头和螺栓式接头。DeviceNet物理层可以选择使用隔离。DeviceNet是基于CAN的现场总线，从技术的角度上来说，其开发不困难。采用的软件DeviceNet方面的软件包有许多种，采用它们可以与产品协同工作，考虑其特性是首要的问题。......
2023-11-22
-
吴淞江商品贸易交通节点详细阅读
通过对吴淞江流域的“因寺成镇”的尹山镇的个案分析，笔者发现它跟其他的“因寺成镇”的市镇比如甪直、南翔等都有明显的不同，其不同不只在于其寺庙的独特，而且其附着在寺庙上的际遇也独特，其地理位置就更独特——正好位于吴淞江和京杭大运河的交汇处，这对于古代主要是靠水运来进行贸易的特点来说，也就决定了尹山能迅速发展，并由寺兴市，进而因市成镇。......
2023-11-18
相关推荐