构建生成树的方法及步骤

2023-07-02 理论教育版权反馈

【摘要】：在介绍具体的生成树构建算法之前，首先作如下定义：ID。为了简便起见，省略根与成员之间的通信过程。第三次迭代时，子树1中的节点1向节点6发出连接请求，成功后节点6加入子树，至此所有节点已全部连接，生成树建立完毕。

在图G中，生成树林（SF）定义为包含G中所有节点且不存在环路的集合，一个生成树林中包括G中所有的不重叠的子生成树（以下简称子树）形成的割集，值得注意的是一个单独的节点也可以被认为是一棵子树。在第一阶段，主要思路是将网络中的子树迭代地合并成为一棵完整的生成树。

在介绍具体的生成树构建算法之前，首先作如下定义：

（1）ID。在第一阶段的开始，给每个节点分配节点ID和子树ID。节点ID用以标识网内各节点，是网内唯一的；子树ID表示节点属于哪个树，规定它等于子树中最低的节点ID，所以，所有位于同一个子树中的节点拥有相同的子树ID。例如，对于单个节点，它的节点ID是i，它的树节点也是i。对于拥有3个节点的子树，它们的节点ID分别是i，j，k，如果满足i＜j＜k，则这3个节点的子树ID均为i。

（2）根。对于一个子树，定义具有最高节点ID的节点为根。假设根能够作为子树的控制中心而具有子树内信息收集的功能，在涉及子树之间的信息交互时具有子树间信息中转的功能。

（3）邻居队列。根据先前的假设，在任意时刻每个节点都掌握其邻居的分布情况和对应边的权重。所以，对于任意子树m，其中所有成员的邻居（除去已经位于m中的邻居），共同形成了一个m的邻居集合。然后依据所有邻居对应的潜在边的权重由小到大进行排序，形成子树m的邻居队列Qm。

（4）信令。阶段1有3种信令信息：REQUEST，RESPONSE，CONNECT，分别表示请求、应答和连接。当节点i试图与j连接时，请求信令REQUEST由i发送到j；如果j同意请求，将返回应答信令RESPONSE消息到i。如果i接收到应答信令，则发出连接信令CONNECT开始连接。

接下来描述算法的主要思想。采用分布式迭代的方法来逐步合并子树，每个子树按各自邻居队列中的顺序依次请求与其他具有更高子树ID的子树连接，直至有一个ID更高的子树与之成功连接。而一旦两个子树连接成功，具有更高节点ID的根就被选作合并之后新的子树的根，相应的，新的子树ID和邻居队列也会被更新。合并子树的过程将迭代至形成一棵完整的树。

在每个子树中，为了避免由于分布式运算的异步性造成的运算结果冲突，运算过程只在根上运行，而其他成员利用子树内的信道向根提供运算参数，并接收和执行根的运算结果。为了简便起见，省略根与成员之间的通信过程。算法包括两个线程。第一个线程叫做listening，运行在所有成员和根节点上，用来监听来自子树ID较低的子树中节点的请求。第二个线程叫做requesting，由根控制各成员节点具体实施，用来按邻居队列顺序向子树ID更高的节点发送请求。

在算法具体的执行层面，子树内成员在根的控制下，可能会向子树ID更高的邻居发送请求。作为接收端，如果存在富余的自由度，根将让节点应答请求；否则，请求被拒绝。应答完毕之后，请求端和应答端将互相连接，它们分别对应的子树也将合并成为一棵更大的子树。一旦两个子树合并，两个子树的根中，节点ID更高的根成为根来接管新的子树，而子树ID和邻居队列也将更新。

一个十分重要的情况是，当一个节点已经达到自由度限制时，节点无法再建立新的链路。但如果这样的节点仍然收到了子树ID较低的邻居发出的请求，令它将向根要求减小它的度以接受这个请求。这种减小度的功能可以称为“降维”。降维功能的细节可以描述为：假设子树m的成员i已经达到了它的自由度极限，现在i要求根协调其他成员来降低自己的度。那么，如果增加一个包含节点i的边e到生成树中，由于树本身的图论特性，增加边e后必然形成一个包含i的环。然后，在这个环路中，删除连接到i上的某条原有的边，从而破坏环路形成新的生成树。如果改进成功，i的度将被减小，从而能够接受新的连接请求。

将提出的建立连接的方法和降维功能结合，就能形成构造生成树的算法，这个算法是完全分布式的。线程listening和requesting的伪代码分别如表6-1和表6-2所示，注意这两个线程是异步平行运行的。

表6-1　listening进程伪代码

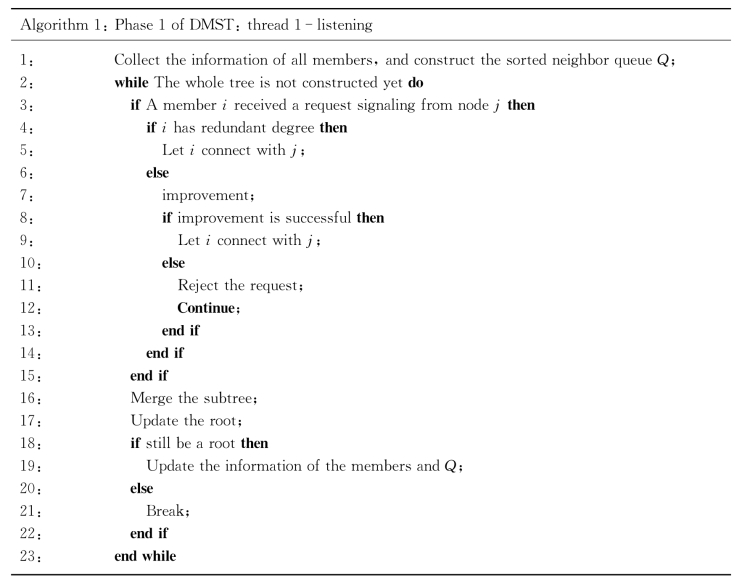
pagenumber_ebook=253,pagenumber_book=239

表6-2　requesting进程伪代码

pagenumber_ebook=254,pagenumber_book=240

表6-2中的运算符“%”表示取余操作，而length（Q）表示队列Q的长度。

图6-2采用一个包括6个节点的网络作为例子来验证算法的正确性。图中圆点表示节点，其中黑色的节点表示“根”；圆点附近括号中的第一个数字表示该节点的节点ID，第二个数字表示该节点的子树ID。图6-2（a）表示网络的初始状态，此时所有节点都尚未连接，各节点的节点ID和子树ID是相同的。在本例子中，根据提出的算法，构建生成树共经历了3个迭代周期。在第一次迭代时，由于节点2在节点1的邻居队列中排在首位，因此节点1向节点2发出连接请求。同理，节点2和节点3分别向节点3和节点4发出连接请求。注意第一次迭代时，节点4，5，6没有发出任何连接请求，这是因为比它们的节点ID高的其他节点都位于它们的通信范围之外，所以在它们的邻居队列中不存在比自己节点ID高的目标节点。连接成功后，形成如图6-2（b）所示的网络结构，此时节点2，3，4的子树ID更新为1。在第二次迭代时，子树1中的节点3按照算法规则向节点5发出连接请求，成功后节点5加入子树1。第三次迭代时，子树1中的节点1向节点6发出连接请求，成功后节点6加入子树，至此所有节点已全部连接，生成树建立完毕。

根据这个例子可以看出，本章提出的构建生成树的算法本质上是一个贪婪启发式算法，本次迭代时，每个子树都尝试连接与本子树具有最短权重链路的潜在邻居节点。根据算法的规则，存在如下定理：

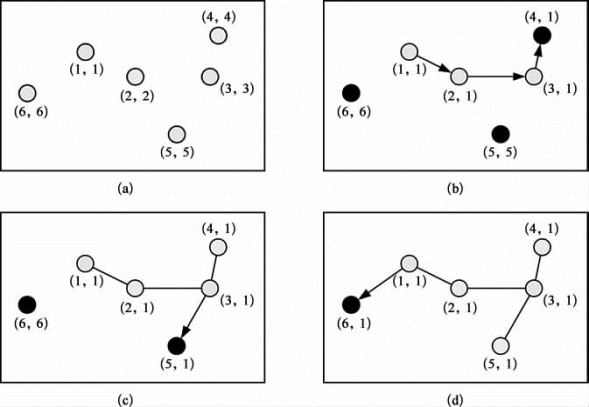
pagenumber_ebook=255,pagenumber_book=241

图6-2　第一阶段的生成树算法示例

（a）节点分布状态；（b）第一次迭代的结果；（c）第二次迭代的结果；（d）第三次迭代的最终结果

定理6-1：只要图G存在连通的可能，则第一阶段的构建生成树算法必然能够构建一棵生成树。

证明：在提出的算法中，更新子树ID的机制确保了每次迭代时每个子树只可能在与其他子树连接时增加一条潜在的边，这就保证了树中不会出现多余的边导致环路的产生。在每一次迭代中，如果自由度限制被满足，至少会增加一个边（当然，这个操作不能保证最优解，即保持平均权重最小）。只有所有的点连接成功，算法才正常终止。因此，算法保证最终构成一个生成树。

构建生成树的方法及步骤

相关推荐