在空间信息网络中，由于星群节点的异构性，不同的节点可能需要不同的连通度来满足不同任务的需要。然而，在一个生成树中，节点的连通度几乎肯定是无法保证的。因此在本节中，将基于一棵最小生成树，通过提出的连通度保证算法，在网络中增加某些额外的边来满足节点连通度的需求，同时算法还需要保持网络中的平均链路权重尽量地小。表6-4节点连通度保证算法伪代码（续表）......
2023-07-02
空间信息网络下的节点逐边调整算法
【摘要】：图的拉普拉斯矩阵及特征值在数学领域有着广泛的研究，尤其是在采用图论和数学规划方法解决网络拓扑构型问题方面。图5-2位于不同轨道的3颗卫星组成的星间组网系统轨道分布情况；星间距离和可视性关系变化规律本章主要考虑空间信息网络中节点分布高动态和节点运算能力有限等星上系统的特点，针对网络初始化和网络重构两种典型场景，通过对拉普拉斯矩阵特征值在矩阵摄动条件下演化规律的分析，得出一种新的逐边调整的启发式算法。
图的拉普拉斯矩阵及特征值在数学领域有着广泛的研究，尤其是在采用图论和数学规划方法解决网络拓扑构型问题方面。在拉普拉斯矩阵所有的特征值中，第二小的特征值（即代数连通度）得到了最深刻的研究和讨论，因为它是衡量网络连通程度好坏的重要指标。为了使网络的连通程度在一定的约束条件下达到最佳，人们通常采用数学规划的方法来最大化网络的代数连通度。但是，代数连通度的最大化问题已被证明是一个NP-hard问题，需要在一定的假设条件下才能转化为凸优化问题或采用启发式算法求解，因此产生了基于不同假设和不同理论的代数连通度最大化算法。
Kim和Mesbahi考虑了加权图中的代数连通度最大化问题，提出了一种基于半正定规划的迭代算法，并通过仿真证明了算法通常可以得到最优解，然而没有考虑动态网络中链路权重变化问题。Kim还考虑了在一个给定图中增加一条边后的代数连通度最大化问题，提出了一种计算效率很高的算法对问题进行了求解。该算法通过优化加入的边的位置，可确保加入一条边后的网络具有最大的代数连通度，为衍生的贪婪算法提供了理论基础。Rafiee和Bayen考虑了多代理网络中两种类型的最优化拓扑设计问题：一是边的数量小于等于给定约束条件下的最大化代数连通度问题；二是代数连通度大于等于给定约束条件下的最小化边的数量问题。两类问题可归纳为一类混合整型半正定规划问题（MISDP），能够通过半正定规划求解软件进行求解。Dai和Mesbahi考虑动态网络在3种情况下的最优化拓扑设计问题：一是边的总数约束条件下的代数连通度最大化问题；二是边的权重约束条件下的代数连通度最大化问题；三是动态场景中的边状态转移时间最小化问题。在离散一致性协议涉及的代数连通度优化问题方面，Xiao和Boyd考虑了分布式均衡协议快速收敛条件下的边权重最优化问题，提出了基于半正定规划的求解算法。
代数连通度在各类网络的设计中都扮演着重要的角色，比如计算机网络、航空运输网络、认知网络、机器人网络、复杂网络和自由空间光通信网络等。另外，代数连通度还涉及网络中的诸如同步、随机行走和泛洪等动态处理的性能。
在代数连通度最大化问题的求解方法方面，凸优化是一个有力的工具，通过对原始问题的松弛化处理，能够得到问题的上界，并且在一定的条件下，该上界是紧的。混合马尔科夫过程对随机网络中的代数连通度演化问题提供了高效的求解方案。通过逐边调整的方法来获得网络最大化代数连通度是各类启发式算法的主要思想。
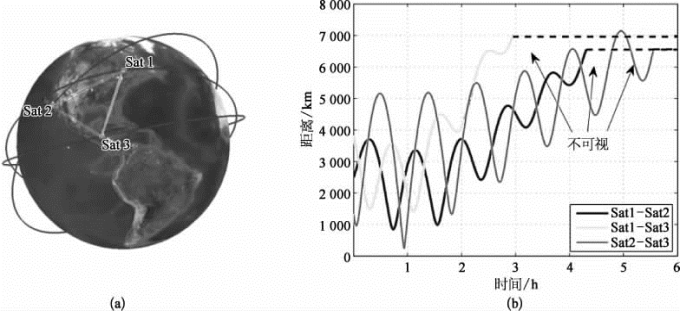
（a）轨道分布情况；（b）星间距离和可视性关系变化规律
本章主要考虑空间信息网络中节点分布高动态和节点运算能力有限等星上系统的特点，针对网络初始化和网络重构两种典型场景，通过对拉普拉斯矩阵特征值在矩阵摄动条件下演化规律的分析，得出一种新的逐边调整的启发式算法。通过数学分析和仿真实验，证明算法的运算结果能够在较小的计算复杂度下实现局部最优化，且与全局最优解之间的误差较小。
有关空间激光微波混合信息网络技术的文章
- 详细阅读
-
节点数量、节点自由度限制和节点连通度需求对算详细阅读
图6-4给出了3种仿真场景下算法得到的最重拓扑，图，，表示3种仿真场景中运行DMST算法得到的近似最优的最小生成树，图，，表示对应的CG算法的结果。在仿真中，仅考虑RC中的可行解来与CG算法比较。图6-7给出了两种算法在3种仿真场景中的运算结果。......
2023-07-02
-
基于节点自由度约束下的最大代数连通度生成树算详细阅读
目前有大量文献针对最小生成树的构造问题进行研究。Zhou等人基于BUA算法，提出了节点自由度约束下的具有最大代数连通度的生成树算法。近年来，除了在网络中寻找具有最小开销的连通链路之外，最小生成树也在其他领域发挥了重要的作用。......
2023-07-02
-
空间信息网络的组网方式详细阅读
表1-1不同业务应用对应的空间网络层次化设计参数按照组网方式不同，可以将天地一体化网络的网络架构归为3大类：天星地网、天基网络、天网地网，不同网络架构的比较如表1-2所示。表1-2美军天基信息系统现状1）天星地网天星地网是目前普遍采用的一种网络结构，包括Inmarsat、Intelsat、宽带全球卫星等系统，其特点是天上卫星之间不组网，而是通过全球分布的地面站实现整个系统的全球服务能力。......
2023-07-02
-
网络初始化问题：边移除算法优化详细阅读
对于网络初始化问题，可以简单地求得其松弛问题的最优解。因此，需要从χ中逐一移除链路，直至其满足整型约束条件。显然，式指出了G′的加权代数连通度的上界。因此，边移除算法的主要思想是每次迭代都从图中移除一条具有最小Δij的边，再对移除后的拓扑进行最优化计算来重新分配链路权重。表5-1边移除算法伪代码（续表）......
2023-07-02
-
网络重构中边增加的算法仿真优化方案详细阅读
从仿真结果中可以看出，提出的边增加算法能够在自由度约束下保持网络的连通性，并使网络在动态状态下保持较高的加权代数连通度。这意味着采用本章提出的算法，每次实施网络重构时仅需调整少数链路即可，大规模地对链路进行调整是没有必要的，同时也反映了边增加算法随k的收敛较快，算法具有实用价值。图5-7边增加算法中不同自由度情况下maxλ2与k的关系......
2023-07-02
-
如何创建下盖的边倒圆特征？详细阅读
图20.7.2 修剪体特征图20.7.2 修剪体特征图20.7.3 定义目标体和刀具体图20.7.3 定义目标体和刀具体Step3.创建图20.7.4b所示的边倒圆特征。选择下拉菜单命令，系统弹出“边倒圆”对话框；在区域中单击按钮，选择图20.7.4a所示的边线为边倒圆参照，并在文本框中输入数值2.5；单击按钮，完成边倒圆特征的创建。......
2023-06-22
-
网络初始化中的边移除算法仿真详细阅读
由于穷举算法在网络规模较小时能够得到问题的精确最优解，因此将提出的边移除算法与穷举算法进行对比，建立一个N=6，d=2的模型来对比穷举算法的精确最优解、边移除算法的上限和边移除算法的次优解。而且，穷举算法消耗的计算时间约为边移除算法计算时间的100倍。接下来，为了考察边移除算法的平均性能，随机构建100个拓扑，每个拓扑中均具有5个节点，但可视性矩阵χ和链路开销矩阵C均随机生成。图5-5边移除算法平均性能......
2023-07-02
相关推荐