加权代数连通度的定义与计算

2023-07-02 理论教育版权反馈

【摘要】：图5-1给出的例子中包括了5个节点组成的不同拓扑的网络结构及其对应的代数连通度。图5-1代数连通度概念示例λ2=0；λ2=0.382 0；λ2=1.382 0；λ2=5代数连通度的最大化问题是图论中一个经典的数学规划问题。在星间组网系统中，考虑到星上资源受限，本章在代数连通度的概念基础上增加了链路权重的因素，将代数连通度扩展为加权代数连通度加以分析。以权重矩阵来计算加权代数连通度的方法与以邻接矩阵来计算非加权代数连通度的方法相同。

由于航天任务的多样性和空间轨位的限制，通常情况下空间信息网络中各星群的空间分布和星群内的节点分布都是不对称的，再加上不同高度的卫星运动速度不同、不同倾角的卫星运动方向不同，导致空间信息网络中卫星节点的空间位置分布呈现大时空尺度、非周期的连续时变状态。这种持续不稳定的节点空间位置分布对空间信息网络的拓扑结构控制带来了极大的挑战。如何在节点之间存在持续高速相对运动的环境下维持网络拓扑的稳定性，成为构建空间信息网络必须解决的重要科学问题之一。

1973年，捷克科学家Miroslav Fiedler在其论文《Algebraic Connectivity of Graphs》中从图论的角度出发，首次提出了代数连通度的相关理论，代数连通度是网络对应的拉普拉斯矩阵的第二小特征值，也被称为Fiedler值或Fiedler特征值。网络的代数连通度是一个标量，反映的是整个网络的连通程度，可用于分析网络的拓扑稳定性和同步能力。代数连通度越大的拓扑结构，网络连通程度越高，网络节点或链路故障对全网连通性的影响越小，网络的稳定性和同步能力越好。

最初的代数连通度概念没有考虑链路的权重因素，对于包含有N个节点的无方向图G中的两个节点i和j，当i与j之间存在直接连接的边时，定义变量a ij=1，否则aij=0。不考虑节点自环的情况，即定义a ii=0，∀i。则由aij为元素的N维对称矩阵A=｛a ij｜i，j∈G｝被称为G的邻接矩阵。另外，定义节点i的“度”d i为连接到i的所有链路的数量，即d i=∑k∈Gaik，将d i作为对角线元素形成的N维对角矩阵D称为网络的度矩阵，则网络对应的拉普拉斯矩阵L可以表示为度矩阵与邻接矩阵之差，即L=D-A。然后对L进行特征分解（也称谱分解），可以得到N个特征值，这N个特征值中0元素的数量表示网络中断开部分的数量；而对于连通的网络，其第二小特征值即为网络的代数连通度，记为λ2。

图5-1给出的例子中包括了5个节点组成的不同拓扑的网络结构及其对应的代数连通度。其中，图5-1（a）的拓扑结构是不连通的，因此其对应的代数连通度等于0，图5-1（b）～（d）中的连通情况越来越好，其对应的代数连通度分别为0.382 0，1.382 0，5。可以看出，连通情况越好的拓扑具有的代数连通度值越大。

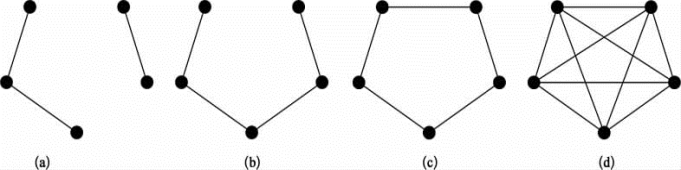
pagenumber_ebook=233,pagenumber_book=219

图5-1　代数连通度概念示例

（a）λ2=0；（b）λ2=0.382 0；（c）λ2=1.382 0；（d）λ2=5

代数连通度的最大化问题是图论中一个经典的数学规划问题。通常在节点和边数量确定的一个图中，通过优化边的分布来使图的代数连通度最大化，这个问题在网络优化中即为面向代数连通度最大化的网络拓扑控制问题。在星间组网系统中，考虑到星上资源受限，本章在代数连通度的概念基础上增加了链路权重的因素，将代数连通度扩展为加权代数连通度加以分析。与非加权代数连通度不同，加权代数连通度中邻接矩阵的元素不是表示连通关系的0-1元素，而是各边的强度权重，通常用w ij表示，形成的矩阵称为权重矩阵。以权重矩阵来计算加权代数连通度的方法与以邻接矩阵来计算非加权代数连通度的方法相同。在空间信息网络中，还需要考虑的是星间相对运动引起的持续星间距离变化和可视性关系变化问题，前者会引起链路权重的变化，后者会导致潜在链路集的变化。图5-2给出了运行于3个不同轨道的卫星之间距离和可视性关系的变化规律。图5-2（a）为这3颗卫星的运行轨道，图5-2（b）为3颗卫星之间的距离和可视性关系变化规律，其中虚线表示卫星之间被地球遮挡导致相互之间不可视。可以看出，在空间信息网络中研究加权代数连通度的优化问题，除了在传统的非加权代数连通度基础上增加链路权重的因素之外，还要考虑链路长度和星间可视性关系动态变化的影响。

加权代数连通度的定义与计算

相关推荐