为了克服π型星座相向运行轨道间缝隙的不足，解决其对地覆盖不均匀的问题，John G.Walker又提出了倾斜轨道卫星星座，由于其轨道面沿赤道面2π弧度圆内均匀分布，又称为2π型星座或者walker delta（δ）倾斜轨道卫星星座，是目前所知覆盖性能最好的星座设计方案。典型代表有Globalstar，Sirius，Skybridge，Celestri和全球定位系统GPS。
2π星座由具有相同轨道高度和倾角的T个卫星组成，P个轨道面在参考面上按升节点均匀分布，每个轨道面内卫星数为T／P，不同轨道平面卫星的相对相位保持一定关系，使相邻轨道卫星分别通过其升节点的时间间隔相等，图4-120（a）为北极俯视图。用4个参数组合i：T／P／F形式表示2π星座，其中i为轨道倾角，F为相位因子且0≤F≤P-1，规定了任意相邻两个轨道面上相邻卫星间的相对位置（相位）。当一个轨道面内卫星通过升交点时，它东面相邻轨道平面内最近一颗卫星通过升交点卫星的相位角为2πF／T，如图4-120（b）所示。
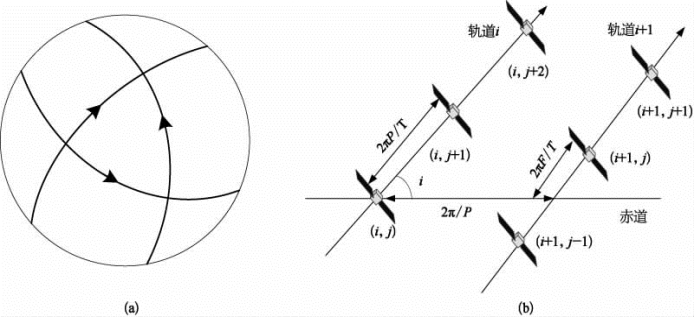
图4-120 2π型星座结构
（a）北极俯视；（b）δ星座定义
第一个轨道面初始时刻升交点赤经Ω1，第一个轨道面第一颗卫星初始时刻纬度幅角ω1，1，则该时刻第i个轨道面上第j个卫星的升交点赤经Ωi和纬度幅角ωi，j分别为
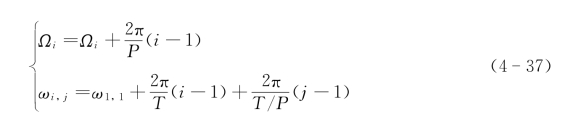
如图4-121所示2π星座逻辑拓扑结构，图4-121（a）为相邻轨道上相同编号卫星间互联逻辑拓扑，图4-121（b）为相邻轨道上相第n个节点和第n+1节点间互联逻辑拓扑。网络逻辑拓扑为网状的曼哈顿街区网络（MSN），每个节点和其上下左右4个节点具有永久性连接。星座轨道面和轨道面上位置两个元素为每个节点赋予一个逻辑编号，例如第n个轨道上第m个卫星表示为（n，m），因此2π型星座在逻辑上具有稳定拓扑，这个特点正好满足了卫星链路组网拓扑结构稳定性的要求，可以极大地简化路由和减少切换。
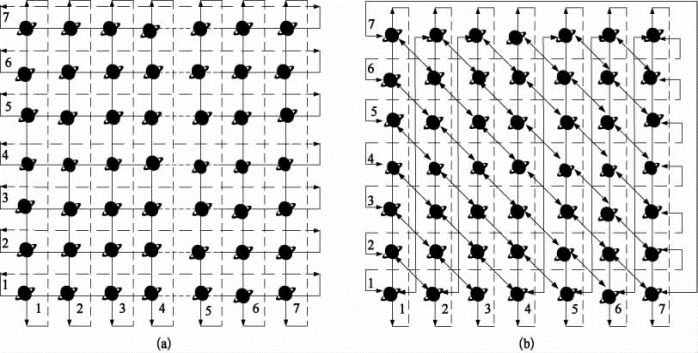
图4-121 2π型星座逻辑拓扑结构
（a）同相位卫星节点互联；（b）异相位卫星节点互联
令ω0表示第一个轨道面的右升节点经度，ω表示第一个轨道面第一颗卫星的初始纬度幅角。以地心为原点建立赤道坐标系，设第n个轨道面上第m个卫星在坐标系中的坐标分别为x n，m，y n，m和z n，m，则有
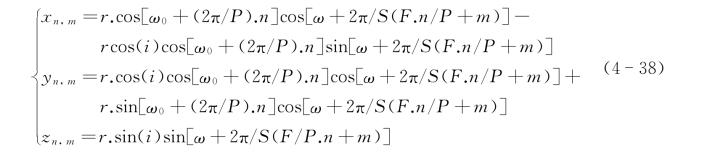
Rosette星座是δ星座中T=P的一种特例，也即每个轨道面上只有一个卫星的星座，用（T，m）来描述，m是Rosette星座的一个重要参数，可取0～（T-1）的任意整数，不同的m就能产生出性能各异的Rosette星座，其覆盖特性也各不相同。星座中任一颗卫星在天球上的位置可以用3个欧拉角来描述，这3个欧拉角分别是升交点赤经Ω、轨道倾角i和相位角ω。由T颗卫星组成的Rosette星座中的第j颗卫星的位置表示为
式中，mΩj为第j颗卫星的初始相位角，n是卫星的平均角速度。
Rosette星座也可以推广到更一般的情况，称为广义Rosette星座，每一个轨道平面内包含S颗卫星，轨道平面数P=T／S，星座可以表示为（T，P，m）。此时，m可取分数：0／S，1／S，2／S，…，（T-1）／S。
有关空间激光微波混合信息网络技术的文章
中轨道卫星系统为非同步卫星系统，由于卫星相对于地面用户的运动，用户与一颗卫星能够保持通信的时间约为100 min。1）Odyssey系统Odyssey系统是TRW公司推出的中轨道卫星通信系统，它的星座系统采用12颗卫星，分布在倾角为55的3个轨道平面上，轨道高度为10 354 km。2）ICO系统ICO系统又称中圆轨道系统，由Inmarsat发起。Spaceway系统采用GEO和MEO的混合结构，总投资30亿～50亿美元，整个系统由包括8颗同步轨道卫星子系统Spaceway EXP和20颗非同步轨道卫星子系统Spaceway NGSO组成。......
2023-07-02
极轨道卫星星座的特征是每条轨道在参考面上有一对公共交点，相邻的同向轨道之间有相同的相对倾角，如图4-118所示北极俯视图。极轨道星座是典型的星形星座，由于升节点均匀分布于赤道平面π弧度半圆范围内，因此又称作π型星座。图4-119π型星座逻辑拓扑北极俯视；两极立体视极轨道卫星星座中，星座犹如一个球面立体栅格覆盖于天球表面，这个网由不同经度的竖直轨道面和不同纬度的水平环组成。......
2023-07-02
分析卫星网络节点的位置和相互运动关系，首先需要确定单颗卫星的轨道参数。卫星轨道参数是描述卫星运行轨道的各种参数。除上述两种轨道外，均称为“倾斜轨道”。在轨运行阶段，卫星在任意时刻其轨道的位置和速度称为卫星星历。图4-4范·艾伦辐射带及典型卫星星座的轨道分布基于以上两点，一般选择的卫星工作轨道高度有3个窗口，即1 000 km上下、10 000 km上下和20 000 km以上。......
2023-07-02
据图4-6的极坐标利用变换：并利用r 0和Φ0表示式（4-6），可得以及利用标准数理推导，可以推导出卫星轨道半径r 0的方程为式中，θ0为常数，e为椭圆的偏心率，椭圆的半焦弦p为式中，h为卫星环绕角动量的大小。轨道方程是椭圆方程，即开普勒行星运动第一定律。根据式可以计算出GEO卫星的轨道半径，此时，周期T等于地球的自转周期，这样才能保证卫星在赤道上的某点与地球保持相对静止状态。......
2023-07-02
按照卫星轨道的高度、倾角、运转周期的不同，可把卫星分为不同的类型。倾斜轨道卫星：0°＜i＜90°，轨道面倾斜于赤道平面。），故轨道的长半轴a=42 164.6／N 2／3 km或42 164.6N 2／3 km；非同步卫星：T≠24或24／N，24N。其轨道称为对地静止轨道，有自然的和人工的两种。LEO卫星分布在500～2 000 km的圆或椭圆轨道上，星座一般由几千颗卫星组成。GEO卫星网络技术成熟，对地覆盖特性好，但是轨道过高，链路容易受损，且传输时延过大。......
2023-07-02
GEO轨道卫星在位于赤道上空、高度约35 786 km的圆轨道上运行，并与地球上的某一点保持相对静止。理论上，单颗GEO轨道卫星的覆盖面积可以达到地球总表面积的三分之一，可以形成一个区域性通信系统，此系统可以为其覆盖范围内的任何一点提供服务。若同时利用3颗卫星便可以构成覆盖除地球南、北极区域的卫星通信系统，因此几乎所有大容量的通信卫星系统都优先选择GEO轨道卫星系统。......
2023-07-02
一方面，低轨道卫星的轨道高度低、传输时延短、路径损耗小，多个卫星组成的星座可以实现真正的全球覆盖，频率复用更有效。因此，LEO系统被认为是最有前途的卫星移动通信系统。Skybridge系统设计的关键是应用了地球静止轨道卫星系统，并采用Ku频段工作，可以满足电信运营商宽带接入的需求，......
2023-07-02
机车在起动时所需的能量非常高，因为只有这样才能拖动车厢并加速至平稳的速度。如果储存的能量足够多，混合动力可以是一个很好的解决方式。铁路设备制造商已经开始研究采用混合动力的机车。据宣称能耗降低了60%，温室气体的排放也相应地降低了。法国SNCF公司在PLATTHEE项目的框架下对混合动力机车进行了测试，测试对象是安装了不同储能系统的转线机车，储能包括蓄电池、超级电容器和飞轮储能。......
2023-06-22
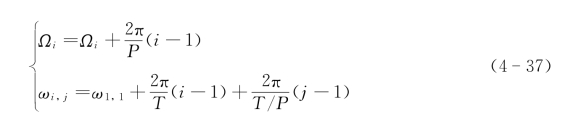
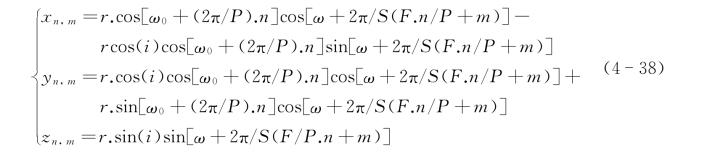
相关推荐