图4-123是多层结构卫星网络拓扑示意图，由LEO／MEO／GEO 3层组成，通过轨间链路把3层连接起来组成一个多层卫星网络结构。3层卫星网络综合考虑了LEO和GEO层的优缺点，其中高层卫星负责网络管理，底层卫星承担业务，一定程度上缓解了信号衰减强、时延大和切换频繁的影响，但由此带来的不足就是系统结构复杂，设计需要谨慎考虑。......
2023-07-02
卫星网络物理拓扑及其结构设计
【摘要】：卫星网络物理拓扑位于空间链路层之上，在整个卫星网络系统设计中具有举足轻重的作用。卫星网络拓扑主要包括单层和多层结构两种。图4-115树形拓扑结构4）超立方体拓扑超立方体互联网络是一个规整对称的网络拓扑。一个n维超立方体含有2n节点。超立方体是一种高度并行、容错能力极强、具有递归结构的网络拓扑，它具有对称性、高连通性、容错性等优良的拓扑特性。图4-116超立方体拓扑结构
卫星网络物理拓扑位于空间链路层之上，在整个卫星网络系统设计中具有举足轻重的作用。物理拓扑结构直接影响节点间ATP、物理信道传输、覆盖特性、路由开销、网络吞吐量、服务质量以及整个系统的复杂性和投资花费，关系到卫星网络能否在激烈的商业化竞争中取得一席之地。卫星网络拓扑主要包括单层和多层结构两种。卫星网络由于卫星运动的特殊性，使其与地面网络又有很多不同的特点。以卫星为节点的网络特点为：①网络各节点的位置以及节点间的相对距离都是以时间为变量的函数；②节点的邻居状况遵循一定的规则；③网络节点总数不会发生变化；④节点间距离比较大，且距离变化也很大，不能忽略；⑤网络的拓扑关系呈周期变化。
根据卫星网络中节点所在轨道的不同可以将网络分为单层网络和分层网络。
单层的全球性或者区域性卫星系统拓扑设计核心的问题就是星座设计，包括极轨道卫星星座、倾斜轨道卫星星座、玫瑰型星座和编队卫星等。随着卫星数目的增多、业务类型的丰富以及业务量的增长，迫切需要能把不同星座系统进行联网组建一个由不同轨道高度卫星组成的多层卫星网络结构，这也是卫星网络物理拓扑设计的核心问题之一。
网络的拓扑结构是抛开网络物理连接来讨论网络系统的连接形式，即网络中各节点的连接方法和形式称为网络拓扑。互联的网络常用一个图G=（N，E）来表示，图中顶点N表示处理机节点的集合，边E表示通信链路的集合。双向通道可以用一条双向边或无向边来表示，单向通道可以用有方向的边来表示。这些网络拓扑往往具有比较好的数学性质，如节点度、直径、规整性、对称性等重要的属性，因此研究网络拓扑结构就归结为研究图的拓扑性质。网络拓扑结构主要有总线结构、环形结构、星形结构、树形结构、网络结构、超立方体结构。
1）线性阵列和环形结构
线性阵列如图4-113所示，是由连续编号的N个节点用双向链路连接构成的。这种网络路由简单，任何节点之间只存在一条路径，因此这种网络没有容错能力。将线性阵列的两端简单连接就形成了环，网络性能得到优化，由于其简单的环形结构、路由策略与低廉的网络成本，早期的局域网多采用环网。但是，在节点规模比较大时，通信时延难以接受。
图4-113 线性阵列和环形拓扑
2）网格结构
将线性阵列和环形拓扑推广到多维时，就得到了多维网格（n-D Mesh）与多维花环（n-d Torus），n表示维数，如图4-114所示。
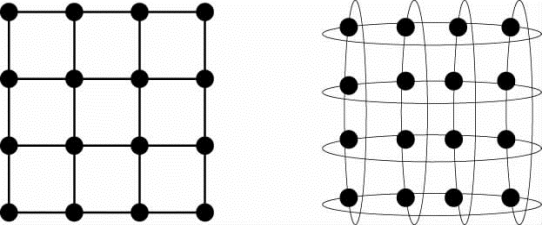
图4-114 二维网格和二维花环拓扑结构
这两种结构在容错性上较线性阵列和环形结构都有很大的提高，它们都是严格正交的，可以用节点在n维空间中的坐标作为节点的编号，因而路由简单。
3）树形拓扑
树作为一种非常简单的拓扑结构，它的直径很小，按对数上升，如图4-115所示。常用的是二叉树。在通信上，树的优点十分明显，随着规模扩大，直径上升幅度很小。树形拓扑的缺点也很突出：因为节点的通信都要靠上层节点完成，所以越靠近根通信越繁忙。在根附近容易形成网络瓶颈。
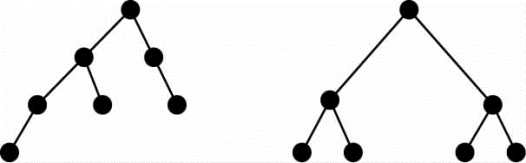
图4-115 树形拓扑结构
4）超立方体拓扑
超立方体互联网络是一个规整对称的网络拓扑。一个n维超立方体含有2n节点。每个节点的地址用n位二进制数表示。任意的两个节点，当且仅当它们的二进制编码地址中有一位不同的时候，两个节点之间才有链路，如图4-116所示。超立方体是一种高度并行、容错能力极强、具有递归结构的网络拓扑，它具有对称性、高连通性、容错性等优良的拓扑特性。
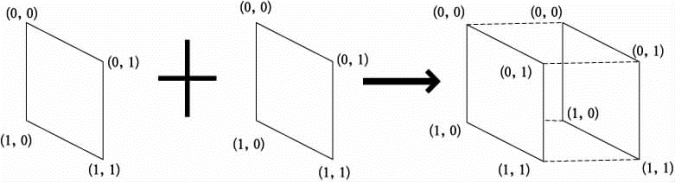
图4-116 超立方体拓扑结构
有关空间激光微波混合信息网络技术的文章
- 详细阅读
-
数据库物理结构设计技巧详细阅读
②对物理结构进行评价，评价的重点是时间和空间效率。如果评价结果满足原设计要求，则可以进入到数据库实施阶段；否则，需要重新设计或修改物理结构，有时甚至要返回到逻辑设计阶段修改数据模式。通常关系数据库的物理结构设计主要包括如下内容。评价物理结构设计的方法完全依赖于具体的DBMS，主要考虑操作开销，即为使用户获得及时、准确的数据所需的开销和计算机资源的开销。......
2023-11-24
-
网络物理拓扑：计算机网络技术基础详细阅读
图1—23星形网络星形拓扑采用集中式通信控制策略，所有的通信均由中央结点控制。图1—24环形网络环形拓扑结构主要具有以下优点：数据传输质量高。单个结点故障会引起整个网络的瘫痪。环形网平时使用的比较少，主要用于跨越较大地理范围的网络，环形拓扑更适用于网间网等超大规模的网络。图1—25树状拓扑网状拓扑又称为无规则拓扑。......
2023-10-22
-
2.5.2 物理冲突及其解决原理详细阅读
2）时间分离将冲突双方在不同的时间段上分离，以降低解决问题的难度。如果冲突的一方可不按一个方向变化，则利用基于条件的分离原理解决冲突是可能的。......
2023-06-26
-
电弧物理特性及其影响因素详细阅读
电弧电压与电流之间的函数关系，首先决定于电弧间隙的物理过程。在许多情况下，电弧热量的散出与电弧在其中燃炽的气体的可动性和导热系数密切相关，试验表明，弧柱电位梯度有随气体导热系数大致成正比上升的倾向。显然，这样的关系仅说明由于热传导而使电弧冷却的电弧特性。后一条曲线低于前一条，这是由于电极和弧柱气体的热惯性所致。所以交流电弧的伏安特性从电阻及其燃炽的特性来看，决不能是完全相同的。......
2023-07-02
-
局域网拓扑结构设计-网络工程与设计详细阅读
逻辑拓扑结构指计算机网络中信息流动的逻辑关系，物理拓扑结构指计算机网络各个组成部分之间的物理连接关系。同一网络的逻辑拓扑结构和物理拓扑结构可能相同，也可能不同。局域网的拓扑结构决定了局域网的工作原理和数据传输方法，一旦选定一种局域网的拓扑结构，则同时需要选择一种适合于该拓扑结构的局域网工作方法和信息的传输方式。目前，局域网的拓扑结构主要有星形、环形、总线型以及网状等。图3-4 网状拓扑结构......
2023-11-25
-
食品物理性污染及其防治措施详细阅读
食品的物理性污染通常指食品生产加工过程中的杂质超过规定的含量，或食品吸附、吸收外来的放射性核素所引起的食品质量安全问题。根据污染物的性质将物理性污染分为两类，即食品的杂物污染和食品的放射性污染。......
2023-07-15
-
计算机网络及其拓扑结构详细阅读
网络拓扑结构、信号方式、访问控制方式、传输介质是影响网络性能的主要因素。网络的拓扑结构是指网络中节点的互联形式。总线型拓扑结构如图2-16所示。图2-16 总线型拓扑结构图2-17 树形拓扑结构......
2023-11-20
相关推荐