图2-43 外圆表面的加工方法的选择1）最终工序为车削的加工方案，适用于除淬火钢以外的各种金属。内孔表面加工方法的选择内孔表面加工方法有钻孔、扩孔、铰孔、镗孔、拉孔、磨孔和光整加工。图2-44 内孔加工方法的选择4）加工精度为IT6级的孔，最终工序采用手铰、精细镗、研磨或珩磨等均能达到要求，视具体情况选择。平面轮廓和曲面轮廓加工方法的选择1）平面轮廓常用的加工方法有数控铣、线切割及磨削等。......
2023-06-26
覆盖性分析：提高测试效率的重要方法
【摘要】：要用某卫星构成一个通信系统，必须先弄清它的覆盖范围。覆盖区的绝对面积S与相对面积S／S 0。对于静止卫星来说，R E+h E=42 164.6 km，利用上述各式可算出全球波束宽度θ1／2=17.4°；星下点到覆盖区边缘所对的地心角α=81.3°；卫星到覆盖区边缘的距离d=41 679.4 km；覆盖面积与总表面积之比S／S 0=42.4%。区域波束覆盖区的几何关系较复杂，必须根据波束主轴的指向与波束截面形状的不同作具体分析。图4-112倾斜轨道卫星S与地球站之间的几何关系
要用某卫星构成一个通信系统，必须先弄清它的覆盖范围。要设计和建立一条卫星通信线路，必须先计算地球站与卫星之间的几何参数，如站对星的距离、站对准卫星时其天线指向的方位角和仰角等，以便进一步求出传输时延和传输损耗。
一般地说，星上天线全球波束的主轴是指向星下点s′的，如图4-110所示，不难求得
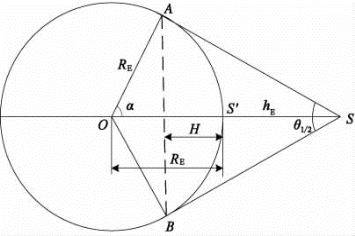
图4-110 全球波束覆盖区的几何关系
（1）卫星的全球波束宽度。
式中，θ1／2为波束的半功率宽度，即卫星对地球的最大视角；R E地球半径（6 378 km）；h E为卫星离地面高度。
（2）覆盖区域边缘所对的最大地心角。
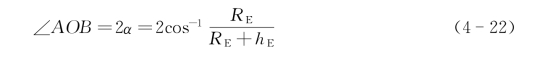
（3）卫星到覆盖区边缘的距离。
（4）覆盖区的绝对面积S与相对面积S／S 0。
式（4-25）中，S=2πR E H是一个球缺的面积（不包括地面），H为球缺的高，S 0=
，即地球的总表面积。
对于静止卫星来说，R E+h E=42 164.6 km，利用上述各式可算出全球波束宽度θ1／2=17.4°；星下点到覆盖区边缘所对的地心角α=81.3°；卫星到覆盖区边缘的距离d=41 679.4 km；覆盖面积与总表面积之比S／S 0=42.4%。
区域波束覆盖区的几何关系较复杂，必须根据波束主轴的指向与波束截面形状的不同作具体分析。对于截面为圆形、主轴对准星下点的区域波束，覆盖区的几何关系可参照图4-111（a）进行分析与计算。例如：当已知波束h E和θ1／2时，其覆盖面积为
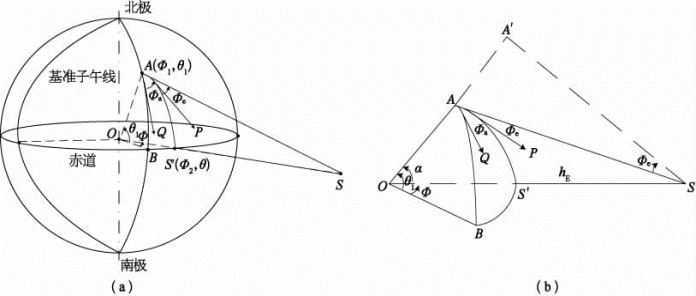
图4-111 静止卫星S与A的几何关系
设地球站A的经纬度为Φ1和θ1，静止卫星S的星下点S′的经纬度为Φ2和θ，这样，则图4-111（a）中的Φ=Φ2-Φ1，为星下点S′对地球站A的经度差。如图4-111（b）所示，弧AS′为过地球站与星下点S′的一段大圆弧，α为该弧所对的地心角；AP为过A站指向S′的一条地平线；∠SAP=Φe，即A站对卫星S的仰角；弧AB为过A站的子午线上的一段弧，B点为子午线与赤道交点；AQ为过A站向正南方的一条地平线；∠QAP=Φa，即A站对卫星S的方位角。在图4-111（b）中，利用几何学和球面三角形的一些基本公式，不难求出：当A站天线对准卫星S时，其仰角Φe、方位角Φa、经度差Φ、地球站纬度θ1的函数关系为
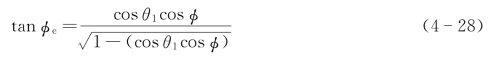
对于静止卫星而言：
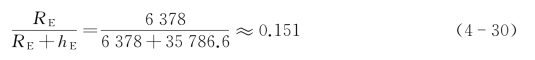
所以
A站到静止卫星S的距离为
由式（4-31）、式（4-32）看出，当θ1一定时，仰角Φe是经度差Φ的偶函数，方位角Φa则是Φ的奇函数；当经度差Φ为0时，Φe出现极大值，Φa则为0°；由于地球站天线的Φe一般不应小于5°，故经度差Φ一般在±90°范围内，其具体范围与θ1有关。
对于不在赤道平面上的非静止卫星，若已知其星下点的某一时刻的经、纬度（Φ2，θ2），θ2＞0°，如图4-112所示，则A站对准卫星的瞬时仰角、方位角，可分别按下式计算：
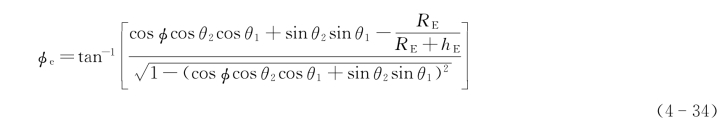
显然，式（4-31）～式（4-33）是式（4-34）～式（4-36）的特例，当卫星趋近赤道平面时，则θ2→0°，α2→Φ，α1→α3→α，这时，式（4-34）～式（4-36）便转化成式（4-31）～式（4-33）了。
图4-112 倾斜轨道卫星S与地球站之间的几何关系
有关空间激光微波混合信息网络技术的文章
- 详细阅读
-
提高金属切割效率的方法详细阅读
锯切也属于冷切割类。锯切分三个变形区。图5-3金属切削原理示意刀具切管机是用车、铣方法切割管材，其原理与锯切方法一样，可以看成是只用少数几个锯齿切管的过程；而砂轮片切管机可以看成是无限多个锯齿切管的过程。其原理与砂轮片切割原理相同，但是具有能切任意形状、低污染、低噪音、切口表面光滑和磨料可以回收循环使用等优点。圆锯片由于效率高、速度快，在锯切中所占的比例最大。......
2023-06-23
-
标准物质在分析测试中的重要性详细阅读
标准物质具有测量标准的属性，在分析测试中起着量值传递、评价分析方法和分析质量控制等作用。对于标准物质，尤其是有证标准物质，广泛用于以下目的［6］。在日常化学分析中，采用相应的标准物质校准分析仪器的测量参数，实现量值的传递是简便和可靠的选择。例如，利用与样品基质相匹配且浓度相近的有证标准物质评价分析方法的偏倚（正确度）。......
2023-06-29
-
如何提高开关电源效率的几个方法详细阅读
5）整流桥的输出电流必须大于开关电源的额定电流，否则电源的功率损耗增大、效率下降，严重时达不到所设计的输出功率。只有适量地提高一次电感LP，才能提高电源的效率。高频变压器的制作工艺降低高频变压器的损耗，是提高电源效率的一项重要措施。这种电流在导线表面流动，中心无电流的现象称为趋肤效应。为了降低铁损，在开关电源空间允许的条件下，可适当选用较大尺寸的铁氧体磁心。......
2023-06-25
-
提高形象，展示仪态礼仪的重要性详细阅读
临到目的地前,那位乘客要求空姐把留言本给他送过去,很显然,他要投诉这名空姐。那位乘客脸色一紧,嘴巴准备说什么,可是没有开口,他接过留言本,开始在本子上写了起来。等到飞机安全降落,所有的乘客陆续离开后,空姐本以为这下完了,可没想到,等她打开留言本,却惊奇地发现,那位乘客在本子上写下的并不是投诉信,而是一封热情洋溢的表扬信。掌握仪容、仪态的相关要求。学会运用仪容、仪态的礼仪技巧。......
2023-07-03
-
厚朴酚及其测试方法分析详细阅读
和厚朴酚与厚朴酚是中药厚朴的主要有效成分，具有抗菌、抑制血小板聚集等作用。测试步骤①标准液的配制：分别准确称取10 mg和厚朴酚与厚朴酚标准品，转入100 mL容量瓶中，加入60 m L甲醇，超声至标准品全部溶解，冷却后再加入甲醇至刻度，摇匀后即可注射。......
2023-07-02
-
姜氏测试方法的分析介绍，详细阅读
姜或姜的提取物一般测试6～10种标志性化合物就足够了，主要有姜辣素、姜烯酚、姜辣二醇和姜辣二酮。HPLC条件色谱柱：Phenomenex LUNA C18，5μm，4.6×250 mm，100 A移动相A：0.1%磷酸水溶液移动相B：0.1%磷酸乙腈溶液流速：1.0 mL／min柱温：室温UV 检测波长：282 nm注射量：20μL梯度：出峰次序：6-姜辣素、辣椒素、8-姜辣素、6-姜烯酚、6-姜辣二醇、6-姜辣二酮、10-姜辣素、8-姜烯酚、10-姜烯酚。......
2023-07-02
-
预习密技：提高学习效率的秘诀详细阅读
在预习过程中，发现疑难点，从而在大脑皮层上引起了一个兴奋中心，即高度集中的注意力状态，提高了学习效率。预习的时间一般要安排在做完当天功课之后的剩余时间，并根据剩余时间的多少，来安排预习时间的长短。......
2023-08-11
相关推荐