首页理论教育卫星轨道方程解析

卫星轨道方程解析

2023-07-02 理论教育版权反馈

【摘要】：据图4-6的极坐标利用变换：并利用r 0和Φ0表示式（4-6），可得以及利用标准数理推导，可以推导出卫星轨道半径r 0的方程为式中，θ0为常数，e为椭圆的偏心率，椭圆的半焦弦p为式中，h为卫星环绕角动量的大小。轨道方程是椭圆方程，即开普勒行星运动第一定律。根据式可以计算出GEO卫星的轨道半径，此时，周期T等于地球的自转周期，这样才能保证卫星在赤道上的某点与地球保持相对静止状态。

人造地球卫星在空间，除了受太阳、月亮、外层大气等因素的作用外，最主要受地球重力的吸引。卫星所以能保持在高空而不坠落，是因为它以适当的速度绕地心不停地飞行。开普勒三定律揭示了卫星受重力吸引而在轨道平面上运动的规律性，即假设卫星的质量为m，它与地心的距离矢量为r，则卫星受到的地球引力为

pagenumber_ebook=152,pagenumber_book=138

式中，M是地球的质量，G=6.672×10-11 N·m2／kg2。由于力=质量×加速度，因而上式可以写为

pagenumber_ebook=152,pagenumber_book=138

根据上两式，可得

pagenumber_ebook=152,pagenumber_book=138

即

pagenumber_ebook=153,pagenumber_book=139

式（4-5）是一个二阶线性微分方程，其解包含6个称为轨道参量的未定常数。由这6个轨道参量所确定的轨道位于一个平面之内，具有恒定的角动量。由于矢量r的二阶微分包含单位矢量r的二阶微分。因此，求解式（4-5）是比较困难的。为了避免求解r的微分，可以选择另一种坐标系，使3个轴方向的单位矢量均为常量。该坐标系以卫星轨道平面为参考面，如图4-5所示。

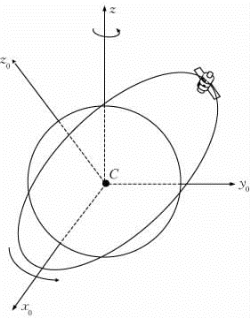
pagenumber_ebook=153,pagenumber_book=139

图4-5　轨道平面坐标系　

pagenumber_ebook=153,pagenumber_book=139

图4-6　卫星轨道平面内的极坐标系

在新坐标系x 0 y 0z 0下，式（4-5）可表示为

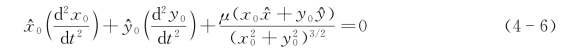
pagenumber_ebook=153,pagenumber_book=139

在极坐标中求解式（4-6）比在笛卡儿坐标中要容易得多，具体极坐标系如图4-6所示。

据图4-6的极坐标利用变换：

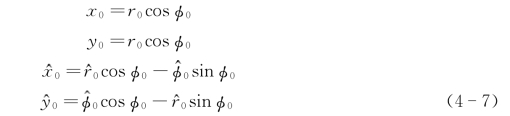
pagenumber_ebook=153,pagenumber_book=139

并利用r 0和Φ0表示式（4-6），可得

pagenumber_ebook=153,pagenumber_book=139

以及

pagenumber_ebook=154,pagenumber_book=140

利用标准数理推导，可以推导出卫星轨道半径r 0的方程为

pagenumber_ebook=154,pagenumber_book=140

式中，θ0为常数，e为椭圆的偏心率，椭圆的半焦弦p为

式中，h为卫星环绕角动量的大小。轨道方程是椭圆方程，即开普勒行星运动第一定律。

式（4-10）中的参量θ0是以轨道平面中轴x 0和轴y 0为参照的椭圆参量。既然已知轨道是椭圆形，通过选择x 0和y 0可以使得θ0等于零。在以下讨论中，可以认为已通过选择x 0和y 0使得θ0等于零，则轨道方程可以表示为

pagenumber_ebook=154,pagenumber_book=140

卫星在轨道平面内运动的轨迹如图4-7所示。长半轴a和短半轴b的值为

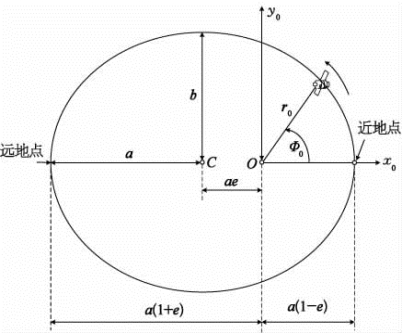
pagenumber_ebook=154,pagenumber_book=140

pagenumber_ebook=154,pagenumber_book=140

图4-7　轨道平面内的运动轨迹

运行轨道中卫星与地球距离最近的点称为近地点，卫星与地球距离最远的点称为远地点。一般而言，近地点和远地点正好相反。为了使θ0=0，必须适当地选择x 0轴，以使近地点和远地点均位于x 0轴上，即选择椭圆的长轴作为x轴。

矢量r 0自卫星运动开始，在G时间内扫过的微分面积为

pagenumber_ebook=155,pagenumber_book=141

注意，h是卫星环绕角动量的大小。由上式可见，在相等时间内，半径矢量扫过的面积是相等的。此即开普勒第二定律。卫星扫过轨道一周的面积即该椭圆的面积（πab），因而可以推导出轨道周期T的表达式为

该式是开普勒行星运动第三定律的数学表达式：环绕周期的平方与长半轴的立方成正比。式（4-16）在卫星通信系统中极为重要。该式可以决定任何卫星的轨道周期，GPS接收机便是利用该式来计算GPS卫星的位置的。根据式（4-16）可以计算出GEO卫星的轨道半径，此时，周期T等于地球的自转周期，这样才能保证卫星在赤道上的某点与地球保持相对静止状态。

要特别注意的是，式（4-16）中环绕周期T是以惯性空间为参照的，即以银河系为参照。轨道周期指的是环绕物体以银河系为参照回到同一参考点所花费的时间。一般而言，被环绕的中心体也是在不停地旋转的，因而卫星的环绕周期与站立在中心体上观测到的周期是不同的。这一点在对地静止卫星（GEO）上表现得尤为明显。GEO卫星的环绕周期与地球的自转周期是相等的，为23 h 56 min 4.1 s，但对地面上的观测者而言，GEO卫星的周期似乎是无穷大的：它总是位于空中的同一位置。