Bergeron数值计算方法与VFTO等效模型简介

2023-07-02 理论教育版权反馈

【摘要】：对于VFTO的计算问题，广大科研工作者多采用列写节点电压、电流方程自编程求解和使用电磁暂态仿真软件进行仿真计算两种方法。（一）Bergeron数值计算法Bergeron数值计算法的核心是把分布参数元件等值为集中参数元件，以便用比较通用的集中参数的数值求解法来计算线路上的波过程。（二）VFTO等效模型自20世纪80年代中期以来，GIS中VFTO相关问题已成为国际高电压领域一个重要的研究课题。

对于VFTO的计算问题，广大科研工作者多采用列写节点电压、电流方程自编程求解和使用电磁暂态仿真软件（Electro-Magnetic Transient Program，EMTP）进行仿真计算两种方法。

EMTP是20世纪50年代由加拿大UBC（不列颠哥伦比亚大学）教授H.W.Dommel创立并经过许多人共同努力、不断完善和发展而成的电磁暂态程序。EMTP基于梯形积分规则，用伴随模型作为动态元件，用节点法建立方程，用稀疏矩阵和LU因式分解法来解代数方程。经过多年发展目前已经成为研究电力系统暂态过程的重要工具之一，在世界范围包括我国在内的大部分电力公司、科研机构、高等学校均在使用。

（一）Bergeron数值计算法

Bergeron数值计算法的核心是把分布参数元件等值为集中参数元件，以便用比较通用的集中参数的数值求解法来计算线路上的波过程。而电路中的集中参数元件L和C也需按数值计算的要求化为相应的等效计算电路。

1.均匀无损线的计算电路

图10-14 单相无损线及等效计算电路

如图10-14a所示的均匀无损线，其波阻为Z，长度为l，波在导线上传播一次的时间为τ，首端和末端的电压及电流分别为u_k（t）、u_m（t）、i_km（t）和i_mk（t）。端点上电流的正方向都取为从端点流向线路。根据混合波的概念，首端在（t-τ）时发出的前行混合波将于t时刻达到线路的末端，因此线路末端的电压和电流可用（t-τ）时首端的电压和电流表示出，即

或写成

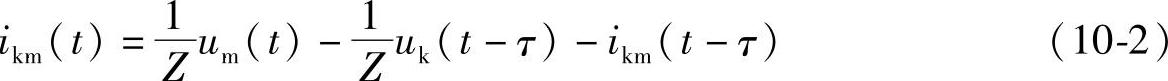
若设

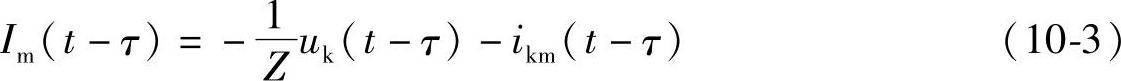
则式（10-2）可写为

根据式（10-4）可以得到端点m在t时刻的等效计算电路，如图10-14b的右端所示。图中Z是阻值等于线路波阻的电阻，I_m（t-τ）是电流源，它可以根据端点k在（t-τ）时刻的电压和电流值从式（10-3）求出。

同样，从反行混合波出发，首端的电压和电流可以用末端在（t-τ）时的电压和电流表示，即

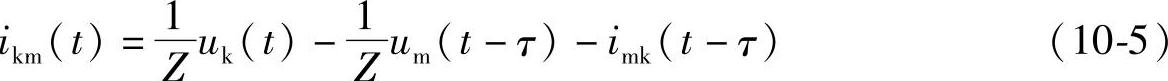
若设

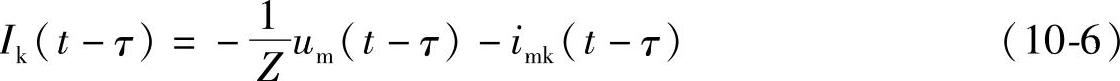
则式（10-5）可写为

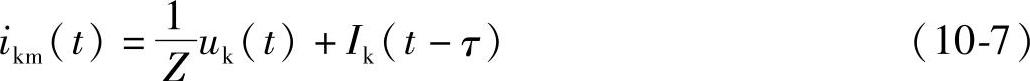
根据式（10-7）可得端点k在t时刻的等值计算电路，如图10-14b的左端所示。电流源I_k（t-τ）可以根据式（10-6）由端点m在（t-τ）时刻的电压和电流求得。

图10-14b等效集中参数电路的特点如下：线路两端点k和m各有自己的独立回路，即端点k和m只由式（10-3）和式（10-6）决定的电流源发生联系，在拓扑上不再有任何联系。在电流源已知的情况下，用节点电位法来解这种电路显然是极为方便的。因此只要知道（t-τ）时刻端点k和m的电压和电流，再利用式（10-3）和式（10-6）求得I_m（t-τ）和I_k（t-τ）后，就可以很容易地求得t时刻节点m和k的电压和电流。

进一步对式（10-7）进行递推计算的结果为

同理，式（10-4）进行递推计算的结果为

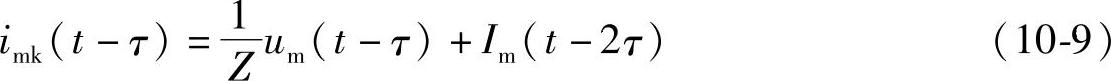
从而得到等效电流源的递推公式为

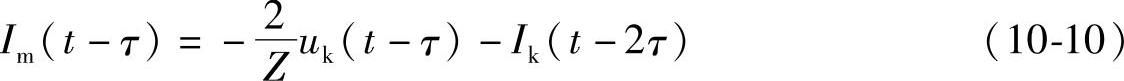
以及

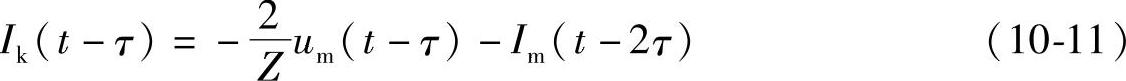
此时I_m（t-τ）和I_k（t-τ）可由（t-τ）时，k点和m点的电压以及（t-2τ）时的I_k和I_m决定，不必再算出端点的电流i_mk（t-τ）及i_km（t-τ），这就可以使计算更为简便。

2.集中参数元件的等效计算电路

先来讨论图10-15a所示的集中参数电感L。

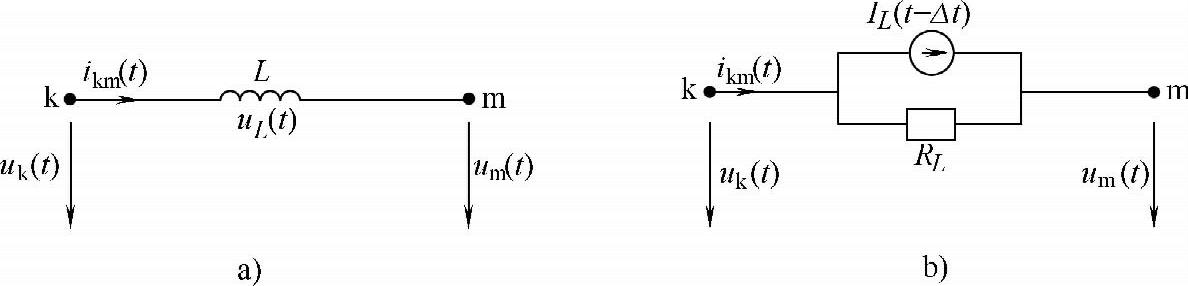
图10-15 电感等效计算电路

电感上的电压u_L（t）和流经电感的电流i_km（t）显然存在以下关系：

用数值计算法求解时，需把时间划分为一系列时间间隔Δt很小的时段，根据（t-Δt）时刻的u_L（t-Δt）和i_km（t-Δt）来求t时刻的u_L（t）和i_km（t）。为此把式（10-12）改写为从（t-Δt）到t的积分形式，即

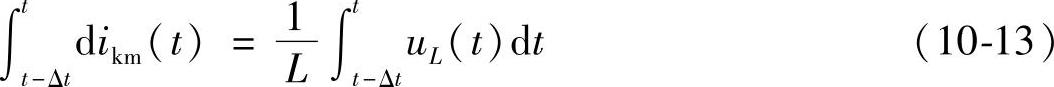
即

对式（10-14）右边用梯形法进行数值积分后可得

考虑到u_L（t）=u_k（t）-u_m（t），式（10-15）可写成

令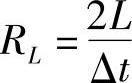，有

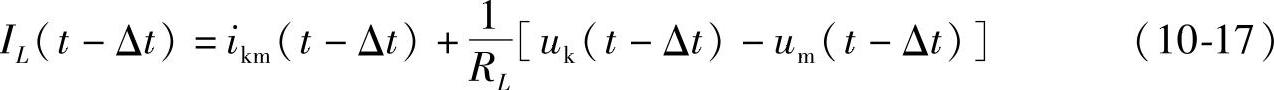
则式（10-16）可改写为

根据式（10-18）可以得到图10-15b所示的电感等效计算电路，其中R_L是电感L的等效计算电阻，只要时间步长Δt确定后，R_L即可求得。I_L（t-Δt）是电感的等值电流源，它可以根据（t-Δt）时刻电感的电流和电压值由式（10-17）求得。

进一步利用对式（10-18）递推计算的结果，即

式（10-17）还可简化为递推公式，即

仿照电感的方法，不难得出图10-16a所示的电容上的电压u_C（t）=u_k（t）-u_m（t）和流经电容的电流i_km（t）间将存在如下关系：

而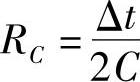，于是有

图10-16 电容等效计算电路

其等值计算电路如图10-16b所示。如果利用递推计算，则等值电流I_C（t-Δt）的计算式也可进一步简化为递推公式，即

至于集中电阻元件，如图10-17所示。

则由于电阻上的电压降u_R（t）=u_k（t）-u_m（t）和流过电阻的电流i_km（t）只由下列方程决定，即

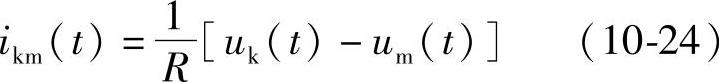
图10-17 电阻电路

而和t以前电阻上的电压降和流经电阻的电流无关，故这一电路无需进一步等值。

（二）VFTO等效模型

自20世纪80年代中期以来，GIS中VFTO相关问题已成为国际高电压领域一个重要的研究课题。一般地，科研人员多采用EMTP进行仿真研究，确定系统的计算模型和相应参数至关重要。GIS开关操作产生的VFTO具有频率高、频率范围广等特点，为保证计算结果精度，需要根据GIS/HGIS各部件结构、布置和接线等，采用空间暂态电磁场分析方法，在VFTO发生的频率范围内对系统各元件进行模拟。表10-1给出了各电压等级下关键元件的等效模型及参数参考值。

表10-1 550kV/800kV/1100kV GIS关键元件的等效模型及参数参考值

Bergeron数值计算方法与VFTO等效模型简介

相关推荐