流体网格法及其在解决激波问题中的应用

2023-07-02 理论教育版权反馈

【摘要】：因此在用流体网格法求解流体动力学方程时，必须考虑对激波的处理，即解决间断的问题。本节在介绍流体网格法以及说明流体网格法差分过程中均提到了差分中的人工粘性系数q，这种加入人工粘性系数的方法目前在跨音速流动的数值计算中是非常有效的。

对于气流场的数值计算方法，一般常用的方法有有限差分法以及有限元法两种：有限差分法是流场数值计算中较为常用的一种数值方法；而有限元法则是近年来引入流场数值计算的一种新方法。但是，有文献指出，有限元法对于解决亚音速流动等气流特性变化较为平缓的气流场问题有较大的优势，其解较为精确且计算程序具有通用性较强的特点，而对于流动中存在激波等现象的流动变化较为剧烈的气流场问题，有限元法的计算结果将难以正确反映这些突变现象。断路器灭弧室内的气体流动恰恰正是具有这种突变的流场，这就限制了有限元法在断路器灭弧室内气流场计算中的应用。

传统的有限差分法有着丰富的内容，经过各国学者多年来的研究、发展，已经相当成熟，对于不同的流场类型、不同的流场结构，有限差分法都有相应的差分网格，而且由于差分网格在构建过程中自动引入了被称为网格粘性的粘性项，如果必要研究人员也可以引入人工粘性项，这些粘性项可以将流动中发生突变的区域拉宽，使之变得较平稳，使数值计算能够捕捉到突变的流动特性。但是，有限差分法在处理场域的复杂边界时存在着很大的困难，原因就在于传统的有限差法对计算区域的剖分是用矩形网格，无法较精确地模拟复杂的场域边界形状，或者用贴体坐标来剖分场域，但是对于很复杂的边界，比如断路器灭弧室的结构，这种方法将是很难实现的。

为了能够利用有限差分法计算有突变流场的优势，并且能够像有限元法一样方便地处理复杂边界，近年来发展了一种适用于任意多边形网格剖分的有限差分法——改进型流体网格法，它能够很好地模拟复杂的场域边界形状。

1.流体网格法的差分格式

流体网格法是一种具有显式差分格式的两步差分法，其中对时间的差分格式是向后差分，而对空间的差分格式则采用了中间差分。由于该方法的差分格式是显式的，不必进行线性方程组的求解，因此求解较方便。在第一步差分中，该方法是把网格当作质团进行拉格朗日运动的计算，忽略了各种输运项对气流特性的影响，仅仅计算流道中的压力梯度对气流速度和内能改变的影响，这一步计算得出的各种流动参数为中间值，分别用、、来表示，它们作为第二步差分计算的起始数据。在第二步计算中，加入各种输运项对流场的影响，按质量、能量和动量守衡的原则将第一步的结果在原来欧拉网格上进行质量、动量和能量的重新分配，得出本时间步内各流动参数的最后结果，完成一个时间步的差分计算，其结果可以作为下一时间步计算的初始数据。

改进型流体网格法的差分格式适用于任意多边形网格的剖分场域，为了以后的介质强度计算部分便于和灭弧室中静电场的计算相结合，以及断路器开断性能数值预测的准确性，灭弧室内气流场计算场域可以被剖分为与有限元法计算电场相同的三角形网格。因此，以下以三角形剖分单元为对象来介绍改进型流体网格法的差分格式。

由以上对流体网格法的介绍可知，流体网格法的一个时间步可分为两个计算步：第一步计算场中的压力效应，得到计算的中间值；第二步计算流动中的输运效应，得到该时间步的最终值。

（1）流体网格法的步骤1

在这一步上由于只计算流动中的压力效应，暂时忽略了电弧数学模型[式（8-75）～式（8-83）]中的输运项和能源项，同时由于只计算压力效应，故在模型中的质量守衡方程可以暂时去掉，因此在第一计算步中，实际是用显式差分格式解如下方程组：

式中 q——人工粘性系数（在以下内容中将详述）；称为对时间的全导数。

图8-44所示是一个典型的三角形格子及其相邻的格子，各符号i、i′、K_i（i=1，2，3）分别表示三角形K的顶点、顶点的对边以及该顶点相对的三角形的编号，S_i为三角形K的第i个顶点的对边的面积（对柱坐标而言，S_i是第i′边绕z轴旋转所围成的曲面的面积）。同时用表示第i′边的长度。通过进行差分，可以求得气流速度的计算中间值、。

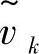图8-44 典型的三角形格子及其相邻的格子

设，各变量在第n时刻为已知，则第n+1时刻差分格式为

式中 u，v——气流的轴向和径向流速；

上角n——第n时刻的相应值；

n1，n2——三角形单元第i′边外法线的单位方向矢量；

A_k——三角形单元K的体积（该三角形单元绕z轴旋转形成的封闭单元的体积）。

在式（8-87）和式（8-88）中的P是P在第i′边上的值，人工粘性系数将在以后的内容中介绍。

利用差分式（8-87）和式（8-88）求得气流速度的中间值、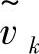后，然后对能量方程

进行差分，进一步求出气体比内能的中间值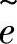，在差分中用M表示K单元中气体的质量，即，差分格式如下：

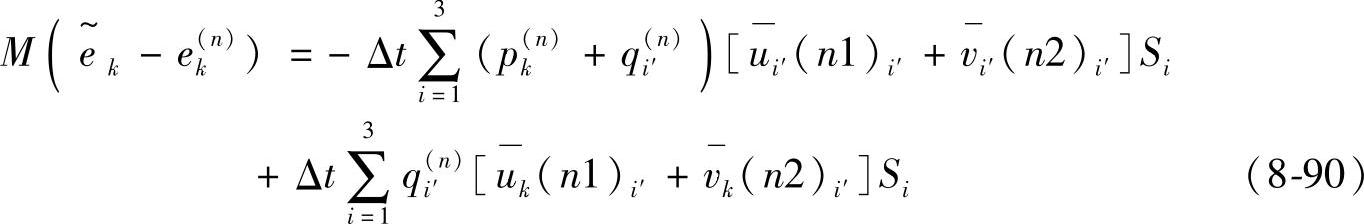
式中；

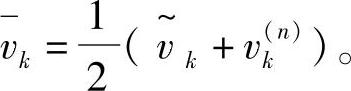
求得后，利用能量公式可以求出气体比总能的中间值如下：

这样就为进行差分的第二步计算作好了数据准备。

（2）流体网格法的步骤2

第二步差分计算是计算通过网格边界从一个网格流到相邻网格的质量、动量和能量输运，同时记入能源项对气体流动的影响。这里采用贡献网格差分来计算输运量。现在假设有一轴矢量Y通过三角形单元K的边界i′，则它的数值DY可以用贡献网格差分计算出来，即

式中——单元K的i′边界上的速度矢量在i′边界法线上投影的值；T_i′——由速度投影的方向来确定，即

在推导出输运量的计算式[式（8-92）]之后，就可以对气体流动过程中的输运量（质量、动量和能量）进行差分计算了。

这样经过第二步的差分计算，就求出了n+1时间步的中值，也是第n+2步的初始值、、、，利用能量公式，即可以求得气体比内能，进而可以从状态方程求出气体的压力，完整的一个时间步的差分就完成了。

2.人工粘性系数q的确定

压气式SF₆断路器灭弧室的气流在开断过程中具有超音速、大畸变的特性，流动过程中将产生激波，激波前后的气流特性将发生阶跃性突变，突变的距离远远小于一个网格的宽度，这样就在流场中产生间断点。因此在用流体网格法求解流体动力学方程时，必须考虑对激波的处理，即解决间断的问题。本节在介绍流体网格法以及说明流体网格法差分过程中均提到了差分中的人工粘性系数q，这种加入人工粘性系数的方法目前在跨音速流动的数值计算中是非常有效的。引入人工粘性系数的指导思想如下：

1）在动量方程和能量方程中加入人工粘性系数可以在流体运动中引进某种人为的耗散机制，使得激波面上的间断解变成一个在相当狭窄的过渡区域内急剧变化却连续的解。

2）由于人工粘性项是外加到方程组中的，因此要求在激波的过渡区以外，人工粘性系数的影响不大，这样就可以不考虑激波的形式和传播，而且在过渡区两侧的力学量还可以近似地满足间断条件。

3）激波过渡区的范围应限制在几个空间步长之内，随着计算的进行不扩大，而且过渡区移动速度应逼近真实的激波速度。

在流体网格法中，为了提高计算的稳定性，在差分格式中采用Landshoff型线性粘度，形式如下：

用差分格式表示为

式中 z_k=（r₁+r₂+r₃）/3；

C_i′——i′边的当地音速；

B——系数，一般不超过0.5。

人工粘性系数只有当马赫数小于并满足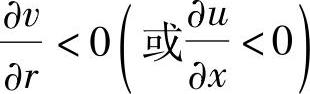时才加入，否则由于有格式粘性而可以不必再加入人工粘性。

3.边界条件的建立

灭弧室内气流场的计算区是在一定边界包围下的区域，其中的流动受着场域边界条件的制约，只是正确处理计算场域的边界条件才可能对灭弧室内的流动进行正确的数值模拟。针对灭弧室，可建立三种边界条件：固壁边界、流出边界、对称轴边界。

（1）固壁边界

图8-45所示是固壁边界在一个网格上的示意图，网格A是流动区域中的网格，网格B是在固壁外假使与网格A相邻的虚拟网格，它们的公共边界是线1，并且两者的体积和面积均相等。对于固壁边界，首先应该保证通过该边界的质量动量和能量的通量为零。

图8-45 固壁边界示意图

进一步确定固壁是绝热的，故而有（n为固壁的外法线方向），这表明单元A和单元B的温度存在T_A=T_B的关系。由固壁通量为零的性质还可以推得e_A=e_B、ρA=ρB、pA=pB，这样固壁的边界条件就确定了。

（2）流出边界图8-46所示是流出边界的示意图，网格B为虚设网格，两个网格的公共边是1，箭头所示为气体的假设流动方向。在气流场的数值计算中，对于流出边界的处理，存在两种意见：一是认为在超音速流动中流出边界可以认为是自由边界，对它不加任何处理，由流动自行解决；二是在流出边界强加背压边界条件。第一种处理方法对于大空间的流动是合适的，但是在断路器灭弧室这样具有复杂的流动在出口取自由边界是不适当的，因为流道背压的大小对流动中激波的产生以及激波的位置是非常重要的，可以认为出口压力是强制压力，即断路器灭弧室中的原始充气压力。其他条件则满足e_A=e_B、ρ_A=ρB、vA=vB。

图8-46 流出边界示意图

（3）对称轴边界

在对称轴上流动也满足通量为零，且对称轴是绝热的，参照固壁边界的处理，则可以得到对称轴的边界条件如下：e_A=e_B、ρ_A=ρ_B、p_A=p_B、u_A=-u_B、v_A=v_B。

4.移动边界的处理

压气式断路器在开断过程中，由压气缸、喷口和动触头组成的部件运动，形成断路器的开断，同时压气缸与固定活塞产生相对运动压缩其中的气体，产生喷口流动，从而达到熄弧的目的。因此，在计算灭弧室内气流场时必须考虑这种压缩过程，以求正确模拟灭弧室内的气体流动。在灭弧室气流场的计算中，采用一种被称作移动网格技术的方法来解决这个问题。为了降低方法实现的难度，可假设断路器在开断过程中的移动部件是形状相对简单的静触头和活塞，而不是实际开断过程中的压气缸、喷口和动触头这些形状复杂的部件。移动网格技术包括网格的消去和网格的生成两部分。网格的消去模拟活塞的压缩过程，在每一时间内，消去紧贴活塞壁面的一列网格，并将这些网格中的质量和压力按体积平均分配给压气缸的其他单元，时间步长逐渐推移，从而实现对压缩过程的模拟。其过程如图8-47所示。

网格的生成用来模拟静触头的开断过程，静触头在每一时间步内移动后空出的区域依照它前面网格的划分规律用网格剖分，这些新的网格中的气体流动参数及气体物性参数与它前面触头未移动前相应的网格的参数相同，从而实现对断路器开断过程的模拟。

图8-47 压气缸压缩过程的模拟

图8-48给出了采用上述计算方法计算的断路器在开断短路电流过程中灭弧室内的气流场动态分布。计算中断路器的额定开断电流为50kA，燃弧时间为15ms。

图8-48 热态流动在电流峰值时的参数分布图

a）等马赫线图 b）等温度线图 c）等密度线图

流体网格法及其在解决激波问题中的应用

相关推荐